[wersja pdf]

[wersja online]
Zapewne przed przeczytaniem całego tego artykułu zadajesz sobie pytanie czy znajdziesz tu poszukiwane informacje. Dlatego poniżej w punktach jest dokładnie napisane co będzie.
Temat jest dosyć trudny, także żeby nie było, że nie mówiłem, chociaż wyjaśnię go najlepiej jak potrafię. Na niektórych kierunkach matematycznych tego nie ma.
Ta teoria jest względnie “świeża” ma zaledwie ponad 100 lat.
Jordan 1838 – 1922
Co będzie?
- Przypomnienie najważniejszych faktów
- Macierz jako przekształcenie liniowe wektora
- Wektory i wartości własne?
- Wielomian i równanie charakterystyczne i widmo macierzy
- Diagonalizacja macierzy
- Czy zawsze macierz jest diagonalizowalna?
- z pojęć nowych
- Co ma rozkład Jordana macierzy do diagonalizacji macierzy?
- Jak wygląda ogólny wzór rozkładu macierzy na postać Jordana?
- Po co dokonywać rozkładu i co on daje?
- Czym różni się zbiór wektorów własnych od przestrzeni własnej?
- W temacie samej macierzy Jordana
- Budowa macierz
- Co to jest klatka Jordana?
- 1,2, czy 3 rodzaje klatek Jordana, czym się różnią?, Jak wyglądają?
- Czy rozkład Jordana jest jednoznaczny?
- Co można pozamieniać, a czego niewolno?
- Co łączy klatki Jordana z wartościami własnymi?
- Czy w rozkładzie może być kilka klatek dla jednej wartości własnej i od czego to zależy?
- Skąd wiadomo ile będzie klatek Jordana dla danej wartości własnej?
- Czym się różni zbiór wektorów własnych o przestrzeni własnej?
- Czym się różni krotność algebraiczna od krotności geometrycznej, wymiaru przestrzeni własnej i z czego wywodzą się te nazwy?
- Budowa macierz
- Macierz
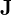 to nie wszystko
to nie wszystko
- Jak budować macierz przejścia?
- Po co są potrzebne wektory dołączone?
- Wektory dołączone, skąd ta nazwa i czy są wektorami własnymi?
- Jak wyznaczać wektory dołączone?
- Czy wektory w macierzy przejścia są niezależne liniowo?
- Co robić gdy wartość własna nie jest rzeczywista?
- Trzeci rodzaj klatek Jordana
- Czym się różni rozkład macierzy o elementach zespolonych na postać Jordana?
- Potęgowanie klatek Jordana?
- Funkcja macierzowa
Zgodnie z obietnicą będą to przykłady z teorią, więc najpierw pokażę Ci jak się to robi, a na koniec podsumujemy teorią.
Dla ustalenia uwagi będę mówił tylko o macierz z elementami rzeczywistymi. Ponadto dla zespolonych postępujemy bardzo analogicznie.
W końcowej części pojawią się nawiązania do jądra odwzorowania liniowego.
Mimo obszernego planu i szczerych chęci, obawiam się, iż temat i tak niezostanie wyczerpany.
Co nie jest konieczne
- Przekształcenia liniowego
- Definicji formalnej przestrzeni liniowej
- Bazy i macierzy przejścia (zmiany bazy)
- Jądra i obrazu przekształcenia liniowego
Chociaż łatwiej będzie ze znajomością.
Dla kogo jest ten materiał
- Gotowych do skupienia
- Chcących zrozumieć i nauczyć się tak często omijanego tematu jakim jest rozkład Jordana macierzy.
- Ciekawych świata
- Zajmujący się teorią sterowania
- Dla inżynierów, zajmujących się inżynierią u “podstaw”
- Które nie chcą być niewolnikiem programu komputerowego, który wszystko oblicza.
Dla kogo nie jest ten materiał
Nie jest dla osób:
- nie potrafiących pomnożyć macierzy
- nie potrafiących obliczyć wyznacznik dowolnego stopnia
- nie potrafiących odwrócić macierzy
- nie potrafiących rozwiązać szkolnego równania wielomianowego
- nie rozumiejących przestrzeni, chociaż na poziomie szkolnym
- nie znających pojęcia kombinacji liniowej wektorów*
- nie jest dla osób preferujących język i styl akademicki
- nastawionych negatywnie i agresywnie, negujących wszystko i wszystkich
Dlaczego Piszę?
- Zdaje sobie sprawę, że temat jest bardzo niszowy i marketingowo strzelam sobie trochę w stopę.
- Mimo to czuje moralny obowiązek podzielenia się tymi informacji, bo też trudno znaleźć je i zebrać do kupy, gdyż są porozrzucane po internecie.
- A niektóre materiały są trudne do zrozumienia przez początkujących
Po co robimy rozkład Jordana
- Aby łatwo i szybko obliczać potęgi wysokiego stopnia z dowolnej macierzy.
 %Potęgi są natomiast kluczem do innych funkcji. Wzór Taylora.
%Potęgi są natomiast kluczem do innych funkcji. Wzór Taylora. - Aby obliczać
 do macierzy% a to spotyka się w równaniach różniczkowych
do macierzy% a to spotyka się w równaniach różniczkowych - Aby obliczać pierwiastek macierzowy% a to przydaje się w teorii sterowania
- Aby obliczać dowolną funkcję od macierzy, która jest rozwijalna w szereg Taylora.
- Zastosowanie przy rozwiązywaniu układu równań różniczkowych
- Zastosowanie w zaawansowanej teorii sterowania.
- W mechanice kwantowej
Macierz Jako przekształcenie liniowe
-
- Wektor
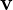 przekształcamy zgodnie z przekształceniem liniowym
przekształcamy zgodnie z przekształceniem liniowym 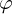 na wektor
na wektor 
- Wektor
![]()
-
- To przekształcenie możemy zastąpić macierzą i vice versa, tzn. dowolną macierz, możemy interpretować jako przekształcenie liniowe wektora, na inny wektor.
- W rachunku macierzowym wykorzystam mnożenie macierzy
![]()
Wektor własny
-
- Pytamy czy jest taki wektor, że po przekształceniu będzie to ten sam wektor lub ewentualnie o zmienionej długości lub zwrocie.
- Wektor taki nazywamy wektorem własnym dla danego przekształcenia liniowego (macierzy).
- Bo są to wektory odporne na to przekształcenie, stąd nazwa wektory własne, bo zdeterminowane przez to dane przekształcenie.
![]()
- Przy czym wykluczamy tu wektor zerowy
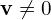
Wartość własna
- Tę liczbę skalującą oznaczamy przez
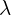 i nazywamy wartością własną. Liczba ta już może być 0.
i nazywamy wartością własną. Liczba ta już może być 0. - To zagadnienie szukania wartości i wektorów własnych nazywa się zagadnieniem własnym.
Zagadnienie własne
-
- Przekształcając można zapisać
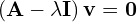
- To co jest istotne, to że dany wektor własny jest przypisany danej wartości własnej
- A takich par wartość własna wektor własny jest wiele dla danego przekształcenia liniowego
- Przekształcając można zapisać
![]()
-
- Chcąc znaleźć wartości i wektory własne najpierw znajdujemy wartości własne.
![]()
Diagonalizacja
-
- Diagonalizacja polega na tym, że daną macierz
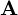 chcemy zapisać w postaci
chcemy zapisać w postaci 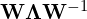 , tzn.
, tzn.
- Diagonalizacja polega na tym, że daną macierz
![]()
Gdzie ![]() jest macierzą diagonalną.
jest macierzą diagonalną.
-
- Nie każda macierz daje się tak zapisać, czyli nie każda macierz jest diagonalizowalna.
- Jeżeli wszystkie wartości własne, są jednokrotne, to taka macierz jest diagonalizowalna. {\tiny {\G{Uwaga na zespolone wartości własne}}}
- Okazuje się, że wektory i wartości własne są bardzo pomocne przy znalezieniu
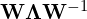
- Wystarczy zbudować macierz
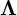 układając na przekątnej wartości własne.
układając na przekątnej wartości własne. - Macierz
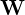 budujemy wstawiając, odpowiadające wektory własne, w tej samej kolejności, co wartości własnym w macierz
budujemy wstawiając, odpowiadające wektory własne, w tej samej kolejności, co wartości własnym w macierz 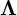
![Rendered by QuickLaTeX.com \[\M{\Lambda} = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \cdots & \lambda_n \\ \end{bmatrix} \qquad \M{W} = \begin{bmatrix} \begin{matrix} \\ \M{v}_1 \\ {} \end{matrix} & \begin{matrix} \\ \M{v}_2 \\ {} \end{matrix} & \begin{matrix} \\ \cdots \\ {} \end{matrix} & \begin{matrix} \\ \M{v}_n \\ {} \end{matrix} \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b99658dcef4ec9ddb30b799458cd93fd_l3.png)
Digonalizowalność
- Jednak jeśli wartości własne nie są jednokrotne to bywa różnie. Czasami macierz jest diagonalizowalna a czasami nie.
- Dokładne omówienie kiedy to jest możliwe, a kiedy nie będziemy dalej dyskutować w tym nagraniu.
- Okazuje się jednak, że każdą macierz można zapisać w postaci Jordana, czyli w zasadzie jest to uogólnienie diagonalizacji.
Rozkład Jordana
-
- Na pierwszy rzut oka wygląda bardzo podobnie
![]()
![Rendered by QuickLaTeX.com \[\M{J} = \begin{bmatrix} \M{K}_1 & \M{0} & \cdots & \M{0} \\ \M{0} & \M{K}_2 & \cdots & \M{0} \\ \vdots & \vdots & \ddots & \vdots \\ \M{0} & \M{0} & \cdots & \M{K}_{\R{q}} \\ \end{bmatrix} \qquad \M{K}_{\R{i}} = \begin{bmatrix} \lambda_{\R{i}} & 1 & 0 & \cdots & 0 \\ 0 & \lambda_{\R{i}} & 1 & \cdots & 0 \\ 0 & 0 & \lambda_{\R{i}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \lambda_{\R{i}} \\ \end{bmatrix},\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-31d508e45bcc7170920a4f58c87b0b4d_l3.png)
gdzie ![]() ,
,
-
- Jednak teraz Macierz
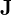 nie jest diagonalna.
nie jest diagonalna. - Macierz
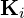 są nazywane klatkami i są różnych stopni.
są nazywane klatkami i są różnych stopni. - Macierz
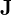 przypomina macierz diagonalną jednak nią nie jest.
przypomina macierz diagonalną jednak nią nie jest. - W istocie składa się z macierzy blokowych o różnych rozmiarach.
- Na przekątnej znajdują się tak zwane klatki, a pozą nią są tylko 0.
- Te klatki zawsze są macierzami kwadratowymi.
- Klatki są dwojakie w zasadzie trojakie, ale po kolei.
- Klatka może być po prostu macierzą
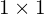 , czyli pojedynczą liczbą.
, czyli pojedynczą liczbą.
- Jednak teraz Macierz
![]()
Diagonalizacja a Rozkład Jordana
- Dla danej wartości własnej też może być wiele klatek.
- Jeżeli macierz
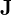 składa się tylko z pojedynczych klatek to wówczas rozkład Jordana daje nam rozkład diagonalny.
składa się tylko z pojedynczych klatek to wówczas rozkład Jordana daje nam rozkład diagonalny. - To jednak bardzo szczególny przypadek, jeśli mamy chociaż jedną wartość własną wielokrotną to niekoniecznie tak musi być.
- Oczywiście pojawia się pytanie jaką klatkę należy wybrać czy jest jeden sposób takiego wyboru itp.
Przykład 1 – wielomian
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 0 & 1 & 0 \\ -4 & 4 & 0 \\ -2 & 1 & 2 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8d82803e2cc044f71664ce93b205b906_l3.png)
\begin{itemize}
Wyznaczamy wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\det \left( \M{A}-\lambda \M{I} \right) = \begin{vmatrix} -\lambda & 1 & 0 \\ -4 & 4-\lambda & 0 \\ -2 & 1 & 2-\lambda \end{vmatrix}= -\lambda(4-\lambda)(2-\lambda) + 4(2-\lambda) =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d4636a244127303e5c006534cb6d563a_l3.png)
![]()
![]()
Przykład 1 – wartości własne
-
- wielomian charakterystyczny
![]()
-
- Wartości własne
![]()
- Krotność algebraiczna wynosi 3
Przykład 1 – Wektory własne
-
- Zagadnienie własne to
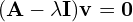
- {\G{Jest to inaczej szukanie jądra, ale przekształcenia}}
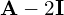
- Zagadnienie własne to
![Rendered by QuickLaTeX.com \[\vspace{-0.5cm} \M{A} = \begin{bmatrix} 0 & 1 & 0 \\ -4 & 4 & 0 \\ -2 & 1 & 2 \end{bmatrix} \qquad \qquad \begin{bmatrix} 0-2 & 1 & 0 \\ -4 & 4-2 & 0 \\ -2 & 1 & 2-2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d304f9e32c3c65a3c5a6cffe7879819b_l3.png)
\begin{itemize}
- Cały układ sprowadza się do jednego równania
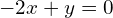
- Wektor własny ogólnie możemy zapisać tak
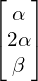 ,
, 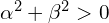
Zbiór wektorów własnych i przestrzeń własna
-
- Zbiór wektorów własnych dla
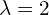 to
to
- Zbiór wektorów własnych dla
![Rendered by QuickLaTeX.com \[\left\{ \begin{bmatrix} \alpha \\ 2\alpha \\ \beta \end{bmatrix} : \alpha^2+\beta^2>0 \wedge \alpha,\beta \in \RR \right\}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0dd77f026743600f1e521ec4094cc53c_l3.png)
-
- Przestrzeń własna dla
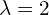 to
to
- Przestrzeń własna dla
![Rendered by QuickLaTeX.com \[\left\{ \begin{bmatrix} \alpha \\ 2\alpha \\ \beta \end{bmatrix} : \alpha,\beta \in \RR \right\}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b06a752e74b568b5f5854e4aa998726b_l3.png)
- Przestrzeń własna różni się tym od zbioru wektorów własnych, że ma dodatkowo wektor zerowy, musi go mieć, bo inaczej nie była by to przestrzeń.
Jakie klatki oraz jaka ich liczba?
-
- Przestrzeń własna jest przestrzenią dwu wymiarową, tzn.
![Rendered by QuickLaTeX.com \[\dim \left(\left\{ \begin{bmatrix} \alpha \\ 2\alpha \\ \beta \end{bmatrix} : \alpha,\beta \in \RR \right\} \right) = 2\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f83133ee1cf316b247d97fedd53df6eb_l3.png)
-
- Zatem będą dwie klatki Jordana
- Skoro krotność algebraiczna wynosi 3 tzn. że musimy mieć jedną klatkę stopnia 1 i jedną klatkę stopnia 2, tzn.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 2 & 1 \\ 0 & 2 \end{bmatrix} \mbox{ oraz } \begin{bmatrix} 2 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2ae40c318d508a7548239664d8c15291_l3.png)
- Bo suma ich stopni musi być równa 3.
Za mało wektorów własnych
-
- Na daną chwilę dysponujemy dwoma niezależnymi liniowo wektorami własnymi
![Rendered by QuickLaTeX.com \[\left\{ \begin{bmatrix} \alpha \\ 2\alpha \\ \beta \end{bmatrix} : \alpha^2+\beta^2>0 \wedge \alpha,\beta \in \RR \right\}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0dd77f026743600f1e521ec4094cc53c_l3.png)
-
- na przykład
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 \\ 2 \\ 0 \end{bmatrix} \mbox{ oraz } \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4a44a6b58c85e488ad4ed7a6335954af_l3.png)
- Natomiast my potrzebujemy 3 wektorów by zbudować macierz
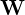
Jak z 2 wektorów zbudować macierz ![]() ?
?
-
- Jak zbudować macierz
- Jak zbudować macierz
![Rendered by QuickLaTeX.com \[\M{W} = \begin{bmatrix} 1 & 0 & ? \\ 2 & 0 & ? \\ 0 & 1 & ? \\ \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3d2a6772aeb60ea193a4d684296f3c69_l3.png)
-
- Potrzebujemy jej do
![Rendered by QuickLaTeX.com \[\M{W}\cdot \M{J}\cdot \M{W}^{-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b2249cf15cbc2d51cbc82d7110e37119_l3.png)
- Potrzebujemy jej do
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 1 & 0 & ? \\ 2 & 0 & ? \\ 0 & 1 & ? \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & ? \\ 2 & 0 & ? \\ 0 & 1 & ? \\ \end{bmatrix}^{-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c2c192afd11cc1b43a4550b51eaa9521_l3.png)
Wektor dołączony
- Skoro wiemy, że mamy klatkę stopnia 2, to będziemy dla niej potrzebowali dwa wektory.
- Chodzi o dwa wektory, które trzeba wstawić do macierz przejścia
 .
. - Potrzeba zatem zrobić z jednego wektora własnego jeden dodatkowy wektory.
- Ten wektor nie będzie już wektorem własnym, ale nadawać się będzie do macierzy
 .
. - Ten “lewy” wektor nazywa się wektorem dołączonym lub wektorem głównym.
Wektor dołączony
-
- Pamiętajmy, że macierz
 będzie odwracana, więc macierz
będzie odwracana, więc macierz 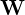 musi mieć wyznacznik niezerowy
musi mieć wyznacznik niezerowy
- Pamiętajmy, że macierz
![]()
- To się sprowadza do pytania czy taki wektor będzie niezależny liniowo z pozostałymi wektorami własnymi?
- Okazuje się, że na szczęście będzie niezależny liniowo i to zawsze.
Wektor dołączony
-
- Aby go znaleźć postępujemy bardzo podobnie.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0-2 & 1 & 0 \\ -4 & 4-2 & 0 \\ -2 & 1 & 2-2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} {\R{0}} \\ {\R{0}} \\ {\R{1}} \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f24abaf2e6c7158e7717c1a17d7df299_l3.png)
-
- tym razem zamiast wektora zerowego wstawiamy wektor własny, z którego chcemy wyprodukować ten nowy “lewy” wektor
![Rendered by QuickLaTeX.com \[\begin{cases} y =2x \\ -2x+y=1 \end{cases} \Rightarrow \mbox{ układ {\R{sprzeczny}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c5f8b35624e3710313dd12bf522ab760_l3.png)
- Czyżby coś było nie tak?
Wektor dołączony
-
- Spróbujmy z drugiego wektora własnego.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0-2 & 1 & 0 \\ -4 & 4-2 & 0 \\ -2 & 1 & 2-2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} {\R{1}} \\ {\R{2}} \\ {\R{0}} \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-706b9b324e09a7b0dc2edb8d41dbb84a_l3.png)
-
- Teraz mamy układ
![Rendered by QuickLaTeX.com \[\begin{cases} -2x+y =1 \\ -4x+2y=2 \\ -2x+y=0 \end{cases} \Rightarrow \mbox{ układ {\R{sprzeczny}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b7fa214bf5a4ffda4a394565fd497ba3_l3.png)
- Znów mamy problem?
Wektor dołączony
-
- Spróbujmy na dowolnym wektorze własnym z tej przestrzeni własnej.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0-2 & 1 & 0 \\ -4 & 4-2 & 0 \\ -2 & 1 & 2-2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} {\R{\alpha}} \\ {\R{2\alpha}} \\ {\R{\beta}} \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-026669512fede70832d0a82ba4a00dd0_l3.png)
-
- Teraz mamy układ
![Rendered by QuickLaTeX.com \[\begin{cases} -2x+y =\alpha \\ -4x+2y=2\alpha \\ -2x+y=\beta \end{cases} \Rightarrow \alpha = \beta\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-7907fd3a67373101370da0a254adb9ae_l3.png)
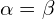 tylko wtedy istniej wektor dołączony
tylko wtedy istniej wektor dołączony
wektor dołączony
-
- Układ sprowadził się do
![]()
-
- Wektor dołączony można w ogólności zapisać tak
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \gamma \\ \alpha + 2\gamma \\ \epsilon \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f241a910099b515cac22e2a6bb513181_l3.png)
-
- Mamy następujący Łańcuch Jordana
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ 2\alpha \\ \beta \end{bmatrix} \to \begin{bmatrix} \gamma \\ \alpha+2\gamma \\ \epsilon \end{bmatrix}_{\begin{tiny} \begin{matrix} \beta =\alpha \end{matrix} \end{tiny}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-59ee54f5f52655a5b461b542c0b6b845_l3.png)
Łańcuch Jordana i podstawianie
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ 2\alpha \\ \beta \end{bmatrix} \to \begin{bmatrix} \gamma \\ \alpha+2\gamma \\ \epsilon \end{bmatrix}_{\begin{tiny} \begin{matrix} \beta =\alpha \end{matrix} \end{tiny}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-59ee54f5f52655a5b461b542c0b6b845_l3.png)
-
- Aby utworzyć parę wektorów dla klatki stopnia 2
![]()
-
- Dostaniemy konkretny wektor własny i wektor dołączony do niego
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}, \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \quad \mbox{ powstaje "bloczek" } \quad \begin{bmatrix} 1 & 0\\ 2 & 1 \\ 1 & 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-33dcc36a8c5a8ce910e269f935eeb3bf_l3.png)
Jaki wektor dla klatki stopnia 1 wybrać?
-
- Dla drugiej klatki, stopnia pierwszego, wystarczy wziąć jakikolwiek wektor własny.
- Oczywiście z tej przestrzeni własnej no i taki, który będzie niezależny liniowo do tego użytego już wektora własnego, czyli do tego

- np.
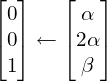
- Teraz możemy zapisać rozkład Jordana macierz
Rozkład Jordana
![]()
-
- W wyniku naszej pracy wytworzyliśmy rozkład Jordana
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & 1 & 0\\ -4 & 4 & 0 \\ -2 & 1 & 2 \end{bmatrix} = \begin{bmatrix} {\ZLO{0}} & {\W{1}} & {\W{0}}\\ {\ZLO{0}} & {\W{2}} & {\W{1}} \\ {\ZLO{1}} & {\W{1}} & {\W{0}} \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{2}} & 0 & 0\\ 0 & {\W{2}} & {\W{1}} \\ 0 & {\W{0}} & {\W{2}} \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{0}} & {\W{1}} & {\W{0}}\\ {\ZLO{0}} & {\W{2}} & {\W{1}} \\ {\ZLO{1}} & {\W{1}} & {\W{0}} \end{bmatrix}^{-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-677dfc95c2d7e977cee0528a898c31e1_l3.png)
Przykład 2 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\hspace{ -0.5cm}\M{A} = \begin{bmatrix} 1 & -3 & 3 \\ -2 & -6 & 13 \\ -1 & -4 & 8 \end{bmatrix} \qquad \qquad \det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 1-\lambda & -3 & 3 \\ -2 & -6-\lambda & 13 \\ -1 & -4 & 8 -\lambda \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-7854a32e39cedb632a33725f528f1583_l3.png)
![]()
![]()
![]()
Przykład 2 wartości własne i wektory własne
-
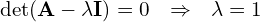 krotność 3
krotność 3- dla
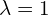
![Rendered by QuickLaTeX.com \[\hspace{ -1.5cm}\M{A} = \begin{bmatrix} 1 & -3 & 3 \\ -2 & -6 & 13 \\ -1 & -4 & 8 \end{bmatrix} \qquad \qquad (\M{A}-{\R{1}}\cdot\M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} 0 & -3 & 3 \\ -2 & -7 &13 \\ -1 & -4 & 7 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1ac1bba3057bf7c88c661874551453dd_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -3y+3z=0 \Rightarrow z= y \\ -2x-7y+13z = 0 \\ -x -4y+7z =0 \end{cases} \Rightarrow x=3y\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4165c9c5174677c0fa47836893277688_l3.png)
Przykład 2 – Wektor własny
-
- Wektor własny jest postaci
![]()
- Wymiar tej przestrzeni własnej jest 1, więc będzie jedna klatka Jordan
- Teraz przejdźmy do wyliczamy wektorów dołączonych
Przykład 2 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & -3 & 3 \\ -2 & -7 &13 \\ -1 & -4 & 7 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3\alpha \\ \alpha \\ \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-37e62106b2a4e473aff7e557fbab7aa0_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -3y+3z= 3\alpha \Rightarrow z= y + \alpha \\ -2x-7y+13z = \alpha \ \Rightarrow \ -2x+6y+13\alpha = \alpha \\ -x -4y+7z = \alpha \ \Rightarrow \ -x+3y+7\alpha = \alpha \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d905da135d5de36e3dce588c2b62350f_l3.png)
-
- Wychodzi zatem
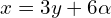 oraz
oraz 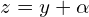
- Wychodzi zatem
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 3\beta + 6\alpha \\ \beta \\ \beta + \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-914fa5705eaadaa6bf2e1262c3d15894_l3.png)
Przykład 2 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & -3 & 3 \\ -2 & -7 &13 \\ -1 & -4 & 7 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3\beta + 6\alpha \\ \beta \\ \beta + \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-371cf19be90a446a3c9201a4fb97bd20_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -3y+3z= 3\beta + 6\alpha \Rightarrow z= y + \beta + 2\alpha \\ -2x-7y+13z = \beta \ \Rightarrow \ x= 3y+6\beta+13\alpha \\ -x -4y+7z = \beta+\alpha \ \Rightarrow \ x= 3y+6\beta+13\alpha \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ff22c6759441086b86c8a74969056f7f_l3.png)
-
- Wektor dołączony jest postaci
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 3\gamma + 6\beta + 3\alpha \\ \gamma \\ \gamma + \beta + 2\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c8f14cb884e50cd2ccf4f32f7d0b9dac_l3.png)
Wybieranie wektorów dla macierzy przejścia
-
- Łańcuch Jordana wygląda tak
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 3\alpha \\ \alpha \\ \alpha \end{bmatrix} \to \begin{bmatrix} 3\beta + 6\alpha \\ \beta \\ \beta + \alpha \end{bmatrix} \to \begin{bmatrix} 3\gamma + 6\beta + 3\alpha \\ \gamma \\ \gamma + \beta + 2\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c9d4362863ee7222c03bea0dde4f799b_l3.png)
-
- Wybieram np.
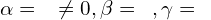 rozkład wygląda tak
rozkład wygląda tak
- Wybieram np.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} {\W{3}} & {\W{6}} & {\W{3}} \\ {\W{1}} & {\W{0}} & {\W{0}} \\ {\W{1}} & {\W{1}} & {\W{2}} \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} {\W{3}} & {\W{6}} & {\W{3}}\\ {\W{1}} & {\W{0}} & {\W{0}} \\ {\W{1}} & {\W{1}} & {\W{2}} \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bc6f6b41719d8596070f377efb05f7f6_l3.png)
Można też inaczej wybrać
-
- Łańcuch Jordana wygląda tak
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 3\alpha \\ \alpha \\ \alpha \end{bmatrix} \to \begin{bmatrix} 3\beta + 6\alpha \\ \beta \\ \beta + \alpha \end{bmatrix} \to \begin{bmatrix} 3\gamma + 6\beta + 3\alpha \\ \gamma \\ \gamma + \beta + 2\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c9d4362863ee7222c03bea0dde4f799b_l3.png)
-
- Równie dobrze
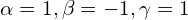 rozkład wygląda tak
rozkład wygląda tak
- Równie dobrze
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 3 & 3 & 0 \\ 1 & -1 & 1 \\ 1 & 0 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 3 & 3 & 0 \\ 1 & -1 & 1 \\ 1 & 0 & 2 \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e852ff24016cab4511adad0b91c7fd29_l3.png)
Co by się stało?
-
- A gdyby policzyć następny wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & -3 & 3 \\ -2 & -7 &13 \\ -1 & -4 & 7 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 3\gamma + 6\beta + 3\alpha \\ \gamma \\ \gamma + \beta + 2\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-84afeb9301712c0ffc77cafa87d92354_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -3y+3z= 3\gamma + 6\beta+13\alpha \Rightarrow z= y + \gamma + 2\beta + \frac{13}{3}\alpha \\ -2x-7y+13z = \gamma \ \Rightarrow \ x= 3y+6\gamma+13\beta+\frac{13^2}{3}\alpha \\ -x -4y+7z = \gamma+\beta+2\alpha \ \Rightarrow \ x= 3y+6\gamma+13\beta+\frac{13\cdot 7-6}{3}\alpha \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2e9b5d4254be48f3704aa9b70b33b080_l3.png)
- Sprzeczność
Przykład 3
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 4 & -5 & 2 \\ 5 & -7 & 3 \\ 6 & -9 & 4 \end{bmatrix} \qquad \det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 4-\lambda & -5 & 2 \\ 5 & -7-\lambda & 3 \\ 6 & -9 & 4-\lambda \end{vmatrix} =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a64b9f191c93dd48a9ea461ff8dcf8e3_l3.png)
![]()
![]()
![]()
- Przejdźmy do równania charakterystycznego
Przykład 3 wartości własne i wektory własne
-
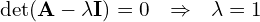 krotność algebraiczna 1
krotność algebraiczna 1- dla
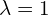
![Rendered by QuickLaTeX.com \[\M{A}=\begin{bmatrix} 4 & -5 & 2 \\ 5 & -7 & 3 \\ 6 & -9 & 4 \end{bmatrix} \qquad (\M{A}-{\R{1}}\cdot\M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} 3 & -5 & 2 \\ 5 & -8 & 3 \\ 6 & -9 & 3 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9c2e578417a1a1474ecd296c5a9b31d1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 3y-5z+2z=0 \Rightarrow z= \frac{5y-3x}{2} \\ 5x-8y+3z = 0 \Rightarrow 5x-8y+\frac{15y-9x}{2}=0 \Rightarrow x-y=0 \\ 6x -9y+3z =0 \Rightarrow 6x-9y+\frac{15y-9x}{2}=0 \Rightarrow 3x-3y=0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-73e84b54475062b33a492fcff34780fd_l3.png)
![]()
Przykład 3 – Wektor własny
-
- wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ \alpha \\ \alpha \end{bmatrix} \qquad \alpha \neq 0\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-05a6c4eb644b248e2a4c3afc227ca017_l3.png)
- Wymiar tej przestrzeni jest 1, więc będzie jedna klatka Jordan
- Tak jest zawsze dla krotności algebraicznej równej 1
Przykład 3 wartości własne i wektory własne
-
 krotność 2
krotność 2- dla
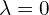
![Rendered by QuickLaTeX.com \[\M{A}=\begin{bmatrix} 4 & -5 & 2 \\ 5 & -7 & 3 \\ 6 & -9 & 4 \end{bmatrix} \qquad(\M{A}-{\R{0}}\cdot\M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} 4 & -5 & 2 \\ 5 & -7 & 3 \\ 6 & -9 & 4 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6563d02826e4f02b6efcde8eb9ac4910_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 4x-5y+2z=0 \Rightarrow 2z= 5y-4x \Rightarrow z=\frac{5y-4x}{2} \\ 5x-7y+3z = 0 \Rightarrow 5x-7y+\frac{15y-12x}{2}=0 \Rightarrow -2x-y=0 \\ 6x -9y+4z =0 \Rightarrow 6x-9y+10y-8x =0 \Rightarrow y-2x=0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-5d9e653bd9efef29a72d5643ab1ce295_l3.png)
![]()
Przykład 3 – Wektor własny
-
- Wektor własny jest postaci
![]()
- Wymiar tej przestrzeni jest 1, więc będzie jedna klatka Jordan
- Krotność algebraicznych
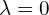 wynosi 2, więc będzie klatka stopnia 2
wynosi 2, więc będzie klatka stopnia 2 - Teraz przejdźmy do wyliczamy wektorów dołączonych
Przykład 3 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 4 & -5 & 2 \\ 5 & -7 & 3 \\ 6 & -9 & 4 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} \beta \\ 2\beta \\ 3\beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2ccf70befa5eb9514838bac609b636f1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} 4x-5y+2z= \beta \Rightarrow 2z= \beta -4x+5y \\ 5x-7y+3z = 2\beta \ \Rightarrow \ 5x-7y+\frac{3\beta-12x+15y}{2} -2\beta = 0 \\ 6x -9y+4z = 3\beta \ \Rightarrow \ 6x-9y+2\beta-8x+10y-3\beta = 0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-02857a85ff7fac8dcfe7fbc824d2d2db_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -2x+y-\beta=0\Rightarrow y=\beta+2x \\ z =3\beta+3x \end{cases} \qquad \begin{bmatrix} \gamma \\ \beta+2\gamma \\ 3\beta + 3\gamma \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2f63864263beccfa7fe6a9ce895b02e1_l3.png)
Wybieranie wektorów dla macierzy przejścia
-
- Łańcuch Jordana wygląda tak
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \beta \\ 2\beta \\ 3\beta \end{bmatrix} \to \begin{bmatrix} \gamma \\ \beta + 2\gamma \\ 3\beta+3\gamma \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-da8efdea3dcf8d85a55cb6d6a4a3d895_l3.png)
-
- Wybieramy
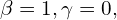 rozkład wygląda tak
rozkład wygląda tak
- Wybieramy
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 1 & 3 & 3 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 1 & 3 & 3 \end{bmatrix}^{-1} = \M{A} = \begin{bmatrix} 4 & -5 & 2 \\ 5 & -7 & 3 \\ 6 & -9 & 4 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-09cd216f3eda85b7cbaf6d26bc663a9b_l3.png)
Przykład 4 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 1 & 1 & 0 & -1 \\ -1 & 3 & 0 & -1 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix} \qquad \det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 1-\lambda & 1 & 0 & -1 \\ -1 & 3-\lambda & 0 & -1 \\ 0 & 0 & 2-\lambda & 0 \\ 0 & 0 & 0 & 2-\lambda \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f5767377985e1981175cb784136d78d5_l3.png)
![Rendered by QuickLaTeX.com \[=\begin{vmatrix} 1-\lambda & 1 \\ -1 & 3-\lambda \end{vmatrix} \cdot (2-\lambda)^2 =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8de05829a3e5444b6d9d1b8b8049d38e_l3.png)
![]()
![]()
Przykład 4 wartości własne i wektory własne
-
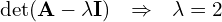 krotność algebraiczna 4
krotność algebraiczna 4- dla

![Rendered by QuickLaTeX.com \[\hspace{-1.1cm} \begin{tiny} \M{A} = \begin{bmatrix} 1 & 1 & 0 & -1 \\ -1 & 3 & 0 & -1 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix} \end{tiny} \qquad (\M{A}-{\R{2}}\cdot\M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} -1 & 1 & 0 & -1 \\ -1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ef506cd62ca0f6b4791a9aba68caa7d0_l3.png)
![]()
Przykład 4 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ \beta \\ \gamma \\ -\alpha+\beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-cd9a3197b106254e1f89588afafb131d_l3.png)
- Więc będą 3 klatki Jordan
- Skoro suma stopni wynosi 4, to będą 3 klatki stopnia 1 i jedna klatka stopnia 2
- Teraz przejdźmy do wyliczamy wektorów dołączonych
Przykład 4 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -1 & 1 & 0 & -1 \\ -1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \alpha \\ \beta \\ \gamma \\ -\alpha+\beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2d0ca55e76c58bed6854c1132ad08749_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x+y-w = \alpha \\ -x+y-w = \beta \\ \gamma = 0 \end{cases} \Rightarrow \alpha=\beta\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3e97ee71f75f517bf4f3f01117b1022d_l3.png)
-
- Wychodzi zatem
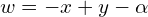
- Wychodzi zatem
![Rendered by QuickLaTeX.com \[\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \begin{bmatrix} \delta \\ \omega \\ \eta \\ -\delta + \omega - \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-06b83a11660d2715328f0535947070d7_l3.png)
Wybieranie wektorów dla macierzy przejścia
-
- Łańcuch Jordana wygląda tak
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ \beta \\ \gamma \\ -\alpha + \beta \end{bmatrix} \to \begin{bmatrix} \delta \\ \omega \\ \eta \\ -\delta + \omega - \alpha \end{bmatrix}_{\begin{tiny} \begin{matrix} \beta =\alpha \\ \gamma = 0 \end{matrix} \end{tiny}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-438d9f542d9210bd201ce2d21c40a459_l3.png)
-
- Wybieramy
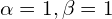 rozkład wygląda tak
rozkład wygląda tak
- Wybieramy
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 & 0 & {\ZLO{1}} & {\ZLO{0}} \\ 0 & 0 & {\ZLO{1}} & {\ZLO{0}} \\ 0 & 1 & {\ZLO{0}} & {\ZLO{0}} \\ -1 & 0 & {\ZLO{0}} & {\ZLO{-1}} \end{bmatrix} \cdot \begin{bmatrix} 2 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & {\ZLO{2}} & {\ZLO{1}} \\ 0 & 0 & {\ZLO{0}} & {\ZLO{2}} \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & {\ZLO{1}} & {\ZLO{0}} \\ 0 & 0 & {\ZLO{1}} & {\ZLO{0}} \\ 0 & 1 & {\ZLO{0}} & {\ZLO{0}} \\ -1 & 0 & {\ZLO{0}} & {\ZLO{-1}} \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c1c62c6f76a402e15502715c9c86e87f_l3.png)
Przykład 5 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 1 & 1 & 9 & -6 \\ -1 & 3 & 11 & -7 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bcf413c4ff1d6f275bbbf241ed15c521_l3.png)
![Rendered by QuickLaTeX.com \[\det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 1-\lambda & 1 & 9 & -6 \\ -1 & 3-\lambda & 11 & -7 \\ 0 & 0 & 2-\lambda & 0 \\ 0 & 0 & 0 & 2-\lambda \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bc34951faaa3ba2577d59c3e72c950a5_l3.png)
![]()
Przykład 5 wartości własne i wektory własne
-
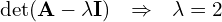 krotność 4
krotność 4- dla

![Rendered by QuickLaTeX.com \[\hspace{-1.5cm}\begin{tiny} \M{A} = \begin{bmatrix} 1 & 1 & 9 & -6 \\ -1 & 3 & 11 & -7 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 2 \end{bmatrix} \end{tiny} \qquad (\M{A}-{\R{2}}\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} -1 & 1 & 9 & -6 \\ -1 & 1 & 11 & -7 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0e16d989906c6884668aaf1bc1355d0d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x + y+9z-6w = 0 \Rightarrow y = x-9z+6w \\ -x+y-11z-7w = 0 \Rightarrow y = x -11z +7w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1a6c6c1f98b4f2585d3a8c2afa68e2c4_l3.png)
![]()
![]()
Przykład 5 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ \alpha+3\beta \\ \beta \\ 2\beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e7ff8a5e69f73e2ad5d117703924fe54_l3.png)
- Więc będą 2 klatki Jordan
- Skoro suma stopni wynosi 4 to:
- 2 klatki stopnia 2
- po jednej klatce stopnia 1 i 3
- Okaże się w trakcie
- Teraz przejdźmy do wyliczamy wektorów dołączonych
Przykład 5 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -1 & 1 & 9 & -6 \\ -1 & 1 & 11 & -7 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \alpha \\ \alpha+3\beta \\ \beta \\ 2\beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ab48535918a668a86393045501e261c7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x+y+9z-6w = \alpha \Rightarrow y = x-9z+6w+\alpha \\ -x+y+11z-7w = \alpha + 3\beta \Rightarrow y=x-11z+7w+\alpha+3\beta \\ 0 = \beta \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad 2z=w+3\cdot 0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9985c45bb704acab63347cb5c8dba913_l3.png)
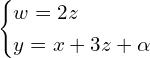 Wówczas
Wówczas 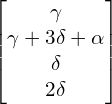
Przykład 5 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -1 & 1 & 9 & -6 \\ -1 & 1 & 11 & -7 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \gamma \\ \gamma + 3\delta+\alpha \\ \delta \\ 2\delta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8a5d72e679009f3b00b9fd62c5eadeb8_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x+y+9z-6w = \gamma \quad \Rightarrow \quad y = x-9z+6w+\gamma \\ -x+y+11z-7w = \gamma + 3\delta +\alpha \quad \Rightarrow \quad y=x-11z+7w+\gamma+\alpha \\ 0 = \delta \qquad \qquad \qquad \qquad \qquad \qquad -9z +6w=-11z+7w+\alpha \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1b34563bd036a039ec1da270fcb881e0_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} w=2z-\alpha \\ y = x+3z-6\alpha+\gamma \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-eb273bb1e760654cdd4896c94d3aecdd_l3.png)
Przykład 5 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{cases} w=2z-\alpha \\ y = x+3z-6\alpha+\gamma \end{cases} \quad \Rightarrow \quad \begin{bmatrix} \omega \\ \omega+3\varphi -6\alpha + \gamma \\ \varphi \\ 2\varphi-\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f893ec8478869c8b83dcb6ae51341207_l3.png)
- Nie szukam dalej, bo już widać, że będzie klatka stopnia przynajmniej 3.
- Skoro tak to wnioskujemy, iż będzie po jednej klatce stopnia 3 i 1
Wybieranie wektorów dla macierzy przejścia
-
- Łańcuch Jordana wygląda tak:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ \alpha+3\beta \\ \beta \\ 2\beta \end{bmatrix} \to \begin{bmatrix} \gamma \\ \gamma + 3\delta+\alpha \\ \delta \\ 2\delta \end{bmatrix}_{\begin{tiny} \begin{matrix} \beta =0 \end{matrix} \end{tiny}} \to \begin{bmatrix} \omega \\ \omega+3\varphi -6\alpha + \gamma \\ \varphi \\ 2\varphi-\alpha \end{bmatrix}_{\begin{tiny} \begin{matrix} \beta =0 \\ \delta = 0 \end{matrix} \end{tiny}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f0b5cdc148753a75b4068582cf9e9b5a_l3.png)
-
- Dla
 klatki stopnia
klatki stopnia 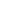 , dla
, dla 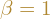 klatka stopnia
klatka stopnia 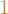
- Rozkład wygląda tak
- Dla
![Rendered by QuickLaTeX.com \[\begin{bmatrix} {\ZLO{0}} & {\W{1}} & {\W{0}} & {\W{0}} \\ {\ZLO{3}} & {\W{1}} & {\W{1}} & {\W{-6}} \\ {\ZLO{1}} & {\W{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{2}} & {\W{0}} & {\W{0}} & {\W{-1}} \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{2}} & 0 & 0 & 0 \\ 0 & {\W{2}} & {\W{1}} & {\W{0}} \\ 0 & {\W{0}} & {\W{2}} & {\W{1}} \\ 0 & {\W{0}} & {\W{0}} & {\W{2}} \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{0}} & {\W{1}} & {\W{0}} & {\W{0}} \\ {\ZLO{3}} & {\W{1}} & {\W{1}} & {\W{-6}} \\ {\ZLO{1}} & {\W{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{2}} & {\W{0}} & {\W{0}} & {\W{-1}} \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8c89d5cf7ccce038441ef03136ca207d_l3.png)
Przykład 6 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 3 & 1 & -4 & -7 \\ -1 & 1 & 5 & 9 \\ 0 & 0 & 4 & 4 \\ 0 & 0 & -1 & 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f80d65a6484a09e649d0b65551cb24f6_l3.png)
![Rendered by QuickLaTeX.com \[\det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 3-\lambda & 1 & -4 & -7 \\ -1 & 1-\lambda & 5 & 9 \\ 0 & 0 & 4-\lambda & 4 \\ 0 & 0 & -1 & -\lambda \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9a0d1df218de852424e331110a414a3e_l3.png)
![]()
Przykład 6 wartości własne i wektory własne
-
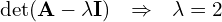 krotność 4
krotność 4- dla

![Rendered by QuickLaTeX.com \[\hspace{-1.7cm}\begin{tiny} \M{A} = \begin{bmatrix} 3 & 1 & -4 & -7 \\ -1 & 1 & 5 & 9 \\ 0 & 0 & 4 & 4 \\ 0 & 0 & -1 & 0 \end{bmatrix} \end{tiny} \quad (\M{A}-2\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} 1 & 1 & -4 & -7 \\ -1 & -1 & 5 & 9 \\ 0 & 0 & 2 & 4 \\ 0 & 0 & -1 & -2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-14e4202e9cd22530b11694bb2cebed43_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x + y-4z-7w = 0 \\ -x-y+5z+9w = 0 \\ z = -2w \end{cases} \Rightarrow \begin{cases} x+y+w =0 \\ -x-y-w =0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4eeeefd33f93c200931b25ca25f18adf_l3.png)
![]()
![]()
Przykład 6 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ -\alpha-\beta \\ -2\beta \\ \beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-34f008332222296ebfc1504e6fcd6b1c_l3.png)
- Więc będą 2 klatki Jordan
- Skoro suma stopni wynosi 4 to:
- 2 klatki stopnia 2
- po jednej klatce stopnia 1 i 3
- Okaże się w trakcie
- Teraz przejdźmy do wyliczamy wektorów dołączonych
Przykład 6 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 & 1 & -4 & -7 \\ -1 & -1 & 5 & 9 \\ 0 & 0 & 2 & 4 \\ 0 & 0 & -1 & -2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \alpha \\ -\alpha-\beta \\ -2\beta \\ \beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0158b955f37fc30935d397bbc79ccaa7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x+y-4z-7w = \alpha \\ -x+y+5z+9w = -\beta-\alpha \\ 2z+4w = -2\beta \end{cases} \Rightarrow \begin{cases} x+ y +w +4\beta = \alpha \\ -x - y-w-5\beta= -\beta -\alpha \\ z = -\beta -2w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-032ec251f8e2a05149c95dca6ad09222_l3.png)
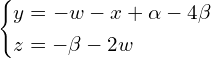 Wówczas
Wówczas 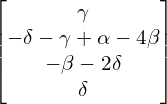
Przykład 6 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 & 1 & -4 & -7 \\ -1 & -1 & 5 & 9 \\ 0 & 0 & 2 & 4 \\ 0 & 0 & -1 & -2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \gamma \\ -\delta-\gamma+\alpha-4\beta \\ -\beta-2\delta \\ \delta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-89fbc05d5be9406ab0afb0cb829a3e8b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x+y-4z-7w = \gamma \\ -x-y+5z+9w = -\delta-\gamma+\alpha-4\beta \\ 2z+4w = -\beta-2\delta \\ -z-2w=\delta \end{cases} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a166f084a9ea388d8ca6c097b05a1d9f_l3.png)
![Rendered by QuickLaTeX.com \[\qquad \qquad \qquad \qquad \qquad \qquad \qquad \begin{cases} x+y+w+4\delta = \gamma \\ -x-y-w-5\delta = -\delta -\gamma +\alpha \\ \beta = 0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3c0c9783fccb4115e9c5e1b2c7ca9fe0_l3.png)
Przykład 6 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\hspace{-0.5cm}\begin{cases} x+y+w+4\delta = \gamma \\ -x-y-w-5\delta = -\delta -\gamma +\alpha \\ \beta = 0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2dd0959cd1551edd9a49f9dd3706aba0_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=-w-4\delta+\gamma -x \\ \alpha = 0 \\ \beta = 0 \end{cases} \quad \Rightarrow \quad \begin{bmatrix} \varphi \\ -\eta - 4\delta + \gamma -\varphi \\ -2\eta - \delta \\ \eta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-beb995b0704d4903801933e38d587ceb_l3.png)
Przykład 6 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \varphi \\ -\eta - 4\delta + \gamma -\varphi \\ -2\eta - \delta \\ \eta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b80bed8101d5756cccaf2643920dcf79_l3.png)
- Widać, że ten już nie zależy od parametrów wektora własnego, tzn.
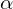 i
i  .
. - Widać zatem, że klatki stopnia 3 nie ma
- Skoro tak to wnioskujemy, iż będzie po jednej klatce stopnia 3 i 1
Wybieranie wektorów dla macierzy przejścia
-
- Łańcuch Jordana wygląda tak:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ -\alpha-\beta \\ -2\beta \\ \beta \end{bmatrix} \to \begin{bmatrix} \gamma \\ -\delta-\gamma+\alpha-4\beta \\ -\beta-2\delta \\ \delta \end{bmatrix} {\G{\to \begin{bmatrix} \varphi \\ -\eta - 4\delta + \gamma -\varphi \\ -2\eta - \delta \\ \eta \end{bmatrix}_{\begin{tiny} \begin{matrix} \beta = 0 \\ \alpha = 0 \end{matrix} \end{tiny}}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a707a8e8a071064cffc86545f25d7cf9_l3.png)
-
- Dla
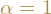 klatki stopnia
klatki stopnia 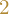 , dla
, dla 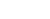 klatka stopnia
klatka stopnia 
- Rozkład wygląda tak
- Dla
![Rendered by QuickLaTeX.com \[\begin{bmatrix} {\ZLO{1}} & {\ZLO{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{-1}} & {\ZLO{1}} & {\W{-1}} & {\W{-4}} \\ {\ZLO{0}} & {\ZLO{0}} & {\W{-2}} & {\W{-1}} \\ {\ZLO{0}} & {\ZLO{0}} & {\W{1}} & {\W{0}} \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{2}} & {\ZLO{1}} & 0 & 0 \\ {\ZLO{0 }}& {\ZLO{2}} & 0 & 0 \\ 0 & 0 & {\W{2}} & {\W{1}} \\ 0 & 0 & {\W{0}} & {\W{2}} \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{1}} & {\ZLO{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{-1}} & {\ZLO{1}} & {\W{-1}} & {\W{-4}} \\ {\ZLO{0}} & {\ZLO{0}} & {\W{-2}} & {\W{-1}} \\ {\ZLO{0}} & {\ZLO{0}} & {\W{1}} & {\W{0}} \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-db2126e48e8ff68dbe89c739f035029d_l3.png)
Przykład 7 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 1 & 1 & 3 & -2 \\ -1 & 3 & 4 & -2 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & -1 & 3 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d3409dc61f5383eba39c609be86710f3_l3.png)
![Rendered by QuickLaTeX.com \[\det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 1-\lambda & 1 & 3 & -2 \\ -1 & 3-\lambda & 4 & -2 \\ 0 & 0 & 1-\lambda & 1 \\ 0 & 0 & -1 & 3-\lambda \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1d4c8a560afea8c42c6c1af240d3eee0_l3.png)
![]()
Przykład 7 wartości własne i wektory własne
-
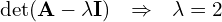 krotność 4
krotność 4- dla

![Rendered by QuickLaTeX.com \[\hspace{-1.5cm}\begin{bmatrix} 1 & 1 & 3 & -2 \\ -1 & 3 & 4 & -2 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & -1 & 3 \end{bmatrix} \qquad (\M{A}-2\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} -1 & 1 & 3 & -2 \\ -1 & 1 & 4 & -2 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8c80e1565b0236958da01133e9731a0d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x + y+3z-2w = 0 \Rightarrow -x+y+z =0 \\ -x-y+4z-2w = 0 \Rightarrow -x+y+2z =0 \\ -z+w = 0 \end{cases} \Rightarrow \begin{cases} y = x \\ z = 0 \\ z = w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e4680a25e4a02d2d9a60630815419d55_l3.png)
Przykład 7 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{cases} y = x \\ z = 0 \\ z = w \end{cases} \qquad \Rightarrow \qquad \begin{bmatrix} \alpha \\ \alpha \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-446874290ba3af6afde368b83b09caad_l3.png)
- Więc będzie 1 klatka Jordan
- Będzie to klatka stopnia 4
- Przejdźmy do wyliczamy wektorów dołączonych
Przykład 7 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -1 & 1 & 3 & -2 \\ -1 & 1 & 4 & -2 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \alpha \\ \alpha \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-5d28baec8b4b381b51930dcf79aa24d3_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x + y+3z-2w = \alpha \\ -x+y+4z-2w = \alpha \\ -z+w = 0 \end{cases} \Rightarrow \begin{cases} x=y-\alpha \\ z =0 \\ z= w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bfbda5df1103c3fd6ebcf2f0dbbea2a1_l3.png)
Wówczas 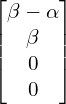
Przykład 7 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -1 & 1 & 3 & -2 \\ -1 & 1 & 4 & -2 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \beta-\alpha \\ \beta \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e0edf62e7ce999b68bf21322d597b2a0_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{ -0.5cm}\begin{cases} -x + y+3z-2w = \beta - \alpha \Rightarrow x=y-\alpha \\ -x+y+4z-2w = \beta \Rightarrow z =0 \\ -z+w = 0 \Rightarrow z= w \end{cases} \Rightarrow \begin{cases} -x+ y +\alpha = \beta - \alpha \\ z = \alpha \\ z=w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c0292708084b910c16e106b3f128de23_l3.png)
Przykład 7 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\hspace{-0.5cm}\begin{cases} -x+ y +\alpha = \beta - \alpha \\ z = \alpha \\ z=w \end{cases} \Rightarrow \begin{cases} y = x + \beta -2 \alpha \\ z=w = \alpha \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-58f58460bef2914f1a278adb80d3ee3e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \gamma \\ \gamma + \beta -2\alpha \\ \alpha \\ \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-349557403c4b50dbd84d3b4d9427c186_l3.png)
Przykład 7 – Wektor dołączony kolejny
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -1 & 1 & 3 & -2 \\ -1 & 1 & 4 & -2 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \gamma \\ \gamma + \beta -2\alpha \\ \alpha \\ \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ab9143ab2434a02cd1967f22f85acfd5_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x + y+3z-2w = \gamma \\ -x+y+4z-2w = \gamma +\beta-2\alpha \\ w = \alpha + z \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-307bdd53ce83c9b0a1021e9341944b27_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x+y+z-2\alpha = \gamma \\ -x+y+2z-2\alpha=\gamma +\beta-2\alpha \\ w = \alpha + z \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-dffb5cc7b0ebe676d0ea03ad2c775f6a_l3.png)
Przykład 7 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\vspace{-0.1cm} \begin{cases} -x+y+z-2\alpha = \gamma \\ -x+y+2z-2\alpha=\gamma +\beta-2\alpha \\ w = \alpha + z \end{cases} \Rightarrow \begin{cases} x = y+z-2\alpha - \gamma \\ x =y+2z-\beta -\gamma \\ w = \alpha + z \end{cases} \Rightarrow\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9711b5dd7bb1398e51e233c40b513e26_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow \begin{cases} x = y+z-2\alpha - \gamma \\ z-2\alpha = 2z-\beta \\ w = \alpha + z \end{cases} \Rightarrow \begin{cases} x = y+z-2\alpha - \gamma \\ z=\beta -2\alpha \\ w =\alpha + z \end{cases} \Rightarrow\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-5040178ef86d7b4c26abe42a74ad4144_l3.png)
![Rendered by QuickLaTeX.com \[\Rightarrow \begin{cases} x =y+ \beta - 4\alpha -\gamma \\ z = \beta -2\alpha \\ w = \beta - \alpha \end{cases} \quad \Rightarrow \quad \begin{bmatrix} \delta + \beta - 4\alpha-\gamma \\ \delta \\ \beta -2\alpha \\ \beta-\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a1238c3015d0b07e51af0f1bdb80bf69_l3.png)
Przykład 7 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \delta + \beta - 4\alpha-\gamma \\ \delta \\ \beta -2\alpha \\ \beta-\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-7e4f535996642b7d7fc1b715c0aeaa8f_l3.png)
- Widać, że taki wektor w dalszym ciągu zależy od parametrów wektora własnego, tzn.
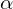 i
i  .
.
Wybieranie wektorów dla macierzy przejścia
-
- Łańcuch Jordana wygląda tak:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ \alpha \\ 0 \\ 0 \end{bmatrix} \to \begin{bmatrix} \beta-\alpha \\ \beta \\ 0 \\ 0 \end{bmatrix} \to \begin{bmatrix} \gamma \\ \gamma + \beta -2\alpha \\ \alpha \\ \alpha \end{bmatrix} \to \begin{bmatrix} \delta + \beta - 4\alpha-\gamma \\ \delta \\ \beta -2\alpha \\ \beta-\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c88de1af384226c19f71ce6898294958_l3.png)
-
- Dla
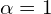 klatka stopnia 4, Rozkład wygląda tak
klatka stopnia 4, Rozkład wygląda tak
- Dla
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 & -1 & 0 & -4 \\ 1 & 0 & -2 & 0 \\ 0 & 0 & 1 & -2 \\ 0 & 0 & 1 & -1 \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 \\ 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 & -1 & 0 & -4 \\ 1 & 0 & -2 & 0 \\ 0 & 0 & 1 & -2 \\ 0 & 0 & 1 & -1 \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-715dbb058aff7dbefb337723031ce2e1_l3.png)
Sposób 2 (szybszy)
-
- Kolejne potęgi macierzy
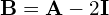
- Kolejne potęgi macierzy
![Rendered by QuickLaTeX.com \[\M{B} = \begin{bmatrix} -1 & 1 & 3 & -2 \\ -1 & 1 & 4 & -2 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \qquad \qquad \M{B}^2 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & -1 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-5aaa6dca758cb2bdaf03672c7ebbd2e3_l3.png)
![Rendered by QuickLaTeX.com \[\M{B}^3 = \begin{bmatrix} 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \qquad \qquad \M{B}^4 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d48e971d79d7596d711200991eb769be_l3.png)
- Teraz wybieramy dowolny wektor, taki aby
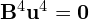 , oraz
, oraz 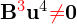
Poprzednie wektory dołączone
-
- Ten wektor to np.
![Rendered by QuickLaTeX.com \[\M{u}^{4} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-fe21deb9c55c10167f7bc13d17b1daff_l3.png)
- Wówczas obliczamy kolejne coraz niższego rzędu wektory dołączone, tzn.
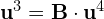
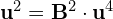
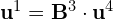
![Rendered by QuickLaTeX.com \[\M{u}^{3}= \M{B} \cdot \M{u}^4 =\begin{bmatrix} -1 & 1 & 3 & -2 \\ -1 & 1 & 4 & -2 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} -2 \\ -2 \\ 1 \\ 1 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6183768f943c1334bd6b541e7bf167ef_l3.png)
![Rendered by QuickLaTeX.com \[\M{u}^{2}= \M{B}^2 \cdot \M{u}^4 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & -1 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-187e2611562fa2ceb4a8089b30cdc710_l3.png)
![Rendered by QuickLaTeX.com \[\M{u}^{1}= \M{B}^3 \cdot \M{u}^4 = \begin{bmatrix} 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-54b2aea45961fcee68723c457f1b8990_l3.png)
Skąd wiadomo w takim razie jakie będą klatki Jordana
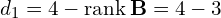
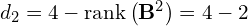
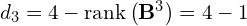
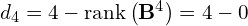
- Jak nam wyszło zero to następne wiadomo, że będzie
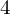
- Klatek będzie
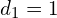
- Klatek stopnia większego od 1 będzie
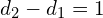
- Klatek stopnia większego od 2 będzie
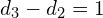
- Klatek stopnia większego od 3 będzie
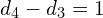
- Klatek stopnia większego od 4 będzie
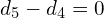
Rozkład Jordana
-
- U kładamy wektory w odpowiedniej kolejności
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 & 1 & -2 & 0 \\ 1 & 2 & -2 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{bmatrix} \cdot \begin{bmatrix} 2 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 \\ 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 2 \end{bmatrix} \cdot \begin{bmatrix} 1 & 1 & -2 & 0 \\ 1 & 2 & -2 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0c085edf1bb2bdf1f0346f4a537ca94f_l3.png)
-
- Czy ten wybór wpasowuję we wcześniej wyznaczony model pierwszą metodą? Łańcuch Jordana wygląda tak:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \alpha \\ \alpha \\ 0 \\ 0 \end{bmatrix} \to \begin{bmatrix} \beta-\alpha \\ \beta \\ 0 \\ 0 \end{bmatrix} \to \begin{bmatrix} \gamma \\ \gamma + \beta -2\alpha \\ \alpha \\ \alpha \end{bmatrix} \to \begin{bmatrix} \delta + \beta - 4\alpha-\gamma \\ \delta \\ \beta -2\alpha \\ \beta-\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c88de1af384226c19f71ce6898294958_l3.png)
Przykład 8 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 0 & -6 & -7 & -9 \\ 1 & 5 & 3 & 4 \\ 0 & 0 & 4 & 2 \\ 0 & 0 & -1 & 1 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1a145518fbb1688f464fd7aacc6b87ed_l3.png)
![Rendered by QuickLaTeX.com \[\det(\M{A}-\lambda\M{I}) = \begin{vmatrix} -\lambda & -6 & -7 & -9 \\ 1 & 5-\lambda & 3 & 4 \\ 0 & 0 & 4-\lambda & 2 \\ 0 & 0 & -1 & 1-\lambda \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-7a39823c6c9be701eb13f211a126760f_l3.png)
![]()
Przykład 8 wartości własne i wektory własne
-
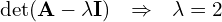 krotność 2 i
krotność 2 i 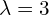 krotność 2
krotność 2- dla

![Rendered by QuickLaTeX.com \[\hspace{-1.52cm}\begin{bmatrix} 0 & -6 & -7 & -9 \\ 1 & 5 & 3 & 4 \\ 0 & 0 & 4 & 2 \\ 0 & 0 & -1 & 1 \end{bmatrix} \qquad (\M{A}-2\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} -2 & -6 & -7 & -9 \\ 1 & 3 & 3 & 4 \\ 0 & 0 & 2 & 2 \\ 0 & 0 & -1 & -1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-cec0262e89e4ef5cb7c2e80fb9044964_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{-1.5cm} \begin{cases} -2x -6y-7z-9w = 0 \Rightarrow -2x-6y-2w =0 \\ x+3y+3z+4w = 0 \Rightarrow x+3y+w =0 \\ 2z+2w = 0 \Rightarrow z=-w \end{cases} \Rightarrow \begin{cases} x = -3y-w \\ z = -w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4e1c47e9cb1a9d11c50910ed3b9ca7e9_l3.png)
Przykład 8 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{cases} x = -3y-w \\ z = -w \end{cases} \qquad \Rightarrow \qquad \begin{bmatrix} -3\alpha-\beta \\ \alpha \\ -\beta\\ \beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4f7649b9eeeaf1fd97c15ad08f4bd0ee_l3.png)
- Będą 2 klatki stopnia 1
Przykład 8 wartości własne i wektory własne
-
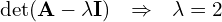 krotność 2 i
krotność 2 i 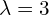 krotność 2
krotność 2- dla
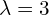
![Rendered by QuickLaTeX.com \[\hspace{-1.52cm}\begin{bmatrix} 0 & -6 & -7 & -9 \\ 1 & 5 & 3 & 4 \\ 0 & 0 & 4 & 2 \\ 0 & 0 & -1 & 1 \end{bmatrix} \qquad (\M{A}-3\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} -3 & -6 & -7 & -9 \\ 1 & 2 & 3 & 4 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & -1 & -2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-7b5ff5fba170ed75b48249ace0c79078_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{-1.5cm} \begin{cases} -3x -6y-7z-9w = 0 \Rightarrow -3x-6y+5w =0 \\ x+2y+3z+4w = 0 \Rightarrow x+2y-2w =0 \\ z+2w = 0 \Rightarrow z=-2w \end{cases} \Rightarrow \begin{cases} -6w+5w=0 \\ x = -2y \\ z = -2w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f139d2542bcc8ea4a2641a888b40d8e1_l3.png)
Przykład 8 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{cases} w=0=z \Rightarrow w=0 \\ x = -2y \\ \end{cases} \qquad \Rightarrow \qquad \begin{bmatrix} -2\alpha \\ \alpha \\ 0\\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a713b4a36f7331327f024434b666c044_l3.png)
- Będą 1 klatki stopnia 2
Przykład 8 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -3 & -6 & -7 & -9 \\ 1 & 2 & 3 & 4 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & -1 & -2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} -2\alpha \\ \alpha \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bd4f355bae76cd2186ef152a25aeb9b7_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -3x -6y-7z-9w = -2\alpha \\ x+2y+3z+4w = \alpha \\ z+2w = 0 \end{cases} \Rightarrow \begin{cases} -3x-6y+5w=-2\alpha \\ x+2y-2w=\alpha \\ z=-2w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-99f32491e97a1e4c9f2e87d36d673b08_l3.png)
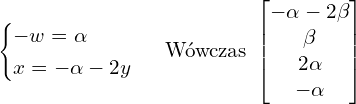
Przykład 8 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -3 & -6 & -7 & -9 \\ 1 & 2 & 3 & 4 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & -1 & -2 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} \beta-\alpha \\ \beta \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b570cb7aec3b0863ec0cd0f772a86495_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -x + y+3z-2w = \beta - \alpha \Rightarrow x=y-\alpha \\ -x+y+4z-2w = \beta \Rightarrow z =0 \\ -z+w = 0 \Rightarrow z= w \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-aac432c01f2f67bd652b72267e159322_l3.png)
Wybieranie wektorów dla macierzy przejścia
-
- Łańcuchy Jordana wyglądają tak:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -3\alpha - \beta \\ \alpha \\ -\beta \\ \beta \end{bmatrix} \qquad \qquad \begin{bmatrix} -2\alpha \\ \alpha \\ 0 \\ 0 \end{bmatrix} \to \begin{bmatrix} -\alpha-2\beta \\ \beta \\ 2\alpha \\ -\alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a4c9bf12dff5b1395d40d99c6f9415d2_l3.png)
-
- dla
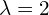 , to
, to  , potem
, potem 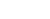
- dla
 , to
, to 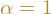
- dla
![Rendered by QuickLaTeX.com \[\begin{bmatrix} {\Y{-3}} & {\W{-1}} & {\ZLO{-2}} & {\ZLO{-1}} \\ {\Y{1}} & {\W{0}} & {\ZLO{1}} & {\ZLO{0}} \\ {\Y{0}} & {\W{-1}} & {\ZLO{0}} & {\ZLO{2}} \\ {\Y{0}} & {\W{1}} & {\ZLO{0}} & {\ZLO{-1}} \end{bmatrix} \cdot \begin{bmatrix} {\Y{2}} & 0 & 0 & 0 \\ 0 & {\W{2}} & 0 & 0 \\ 0 & 0 & {\ZLO{3}} & {\ZLO{1}} \\ 0 & 0 & {\ZLO{0}} & {\ZLO{3}} \end{bmatrix} \cdot \begin{bmatrix} {\Y{-3}} & {\W{-1}} & {\ZLO{-2}} & {\ZLO{-1}} \\ {\Y{1}} & {\W{0}} & {\ZLO{1}} & {\ZLO{0}} \\ {\Y{0}} & {\W{-1}} & {\ZLO{0}} & {\ZLO{2}} \\ {\Y{0}} & {\W{1}} & {\ZLO{0}} & {\ZLO{-1}} \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-10f665f7c1ed84121826b6de9e5a7515_l3.png)
Przykład 9
-
- To może stopnia 6
![Rendered by QuickLaTeX.com \[A = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 1 \\ -1 & -1 & 1 & 1 & -1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9371be1f00001b658643e2b626ddb511_l3.png)
Przykład 9 – wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\det(\M{A}-\lambda \M{I})= \begin{vmatrix} 1-\lambda & 0 & 0 & 0 & 0 & 0 \\ 0 & -\lambda & 0 & 0 & -1 & 1 \\ -1 & -1 & 1-\lambda & 1 & -1 & 1 \\ 0 & 0 & 0 & 1-\lambda & 0 & 0 \\ 0 & 1 & 0 & 0 & 2-\lambda & 0 \\ 0 & 0 & 0 & 0 & 0 & 1-\lambda \\ \end{vmatrix} =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-788dc77d03060ecc14f09206fc2b2f4e_l3.png)
![Rendered by QuickLaTeX.com \[= (1-\lambda)^2\cdot \begin{vmatrix} -\lambda & 0 & 0 & -1 \\ -1 & 1-\lambda & 1 & -1 \\ 0 & 0 & 1-\lambda & 0 \\ 1 & 0 & 0 & 2-\lambda \\ \end{vmatrix} =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f61e1b1657eebdd3346a57cf29ed32e7_l3.png)
Przykład 9 – wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[= (1-\lambda)^2\cdot \begin{vmatrix} -\lambda & 0 & 0 & -1 \\ -1 & 1-\lambda & 1 & -1 \\ 0 & 0 & 1-\lambda & 0 \\ 1 & 0 & 0 & 2-\lambda \\ \end{vmatrix} = (1-\lambda)^3\cdot \begin{vmatrix} -\lambda & 0 & -1 \\ -1 & 1-\lambda & -1 \\ 1 & 0 & 2-\lambda \\ \end{vmatrix} =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0d02ca0f4b5654b9376f0e2bb9e597de_l3.png)
![Rendered by QuickLaTeX.com \[= (1-\lambda)^4 \begin{vmatrix} -\lambda & -1 \\ 1 & 2-\lambda \\ \end{vmatrix} = (1-\lambda)^6\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-77af5d90624adeb76372f3137af1f154_l3.png)
![]()
Przykład 9 – wektory własne
-
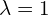 Zagadnienie własne to
Zagadnienie własne to 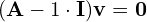
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & -1 & 1 \\ -1 & -1 & 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \\ t \\ s \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e1fa85600dd3ba848d1f175905d9c36b_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -y-t+s=0 \quad \Rightarrow \ s=0 \\ -x-y+w-t+s = 0 \quad \Rightarrow \ w=x \\ y+t = 0 \quad \Rightarrow \ y=-t \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-49dc1803dd57da043185ef8b4dda3355_l3.png)
Przykład 9 – wektory własne
![Rendered by QuickLaTeX.com \[\begin{cases} s = 0 \\ w = x \\ y = -t \end{cases} \Rightarrow \begin{bmatrix} \alpha \\ -\beta \\ \gamma \\ \alpha \\ \beta \\ 0 \end{bmatrix}, \mbox{ gdzie } \alpha^2+\beta^2 +\gamma^2>0\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-261ca265258dc124214f747f73b52bb2_l3.png)
- Możemy wybrać do 3 wektorów własnych liniowo niezależnych

- Będą zatem 3 klatki Jordana. Możliwe konfiguracje
 , która dokładnie okaże się w trakcie.
, która dokładnie okaże się w trakcie.
Wektor dołączony (2)
-
- Tak czy siak będzie potrzebny wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & -1 & 1 \\ -1 & -1 & 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \\ t \\ s \end{bmatrix} = \begin{bmatrix} \alpha \\ -\beta \\ \gamma \\ \alpha \\ \beta \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d74574ffd9d7521f80e9177e683c2382_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} {\R{0 = \alpha }} \\ -y-t+s=-\beta \quad \Rightarrow \ s=0 \\ -x-y+w-t+s = \gamma \quad \Rightarrow \ w=\gamma+\beta + x \\ y+t = \beta \quad \Rightarrow \ y=-t+\beta \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e535653800e45d773a5c95df42c9ffdb_l3.png)
Wektory dołączone (2)
![Rendered by QuickLaTeX.com \[\begin{cases} {\R{0 = \alpha }} \\ s = 0 \\ w = \gamma+\beta+x \\ y = -t+\beta \end{cases} \Rightarrow \begin{bmatrix} \delta \\ -\varphi+\beta \\ \epsilon \\ \gamma + \beta + \delta \\ \varphi \\ 0 \end{bmatrix}, \mbox{ gdzie } {\R{0}}^2+\beta^2 +\gamma^2>0\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ab4e5edf691da0d3f621ade41909fa84_l3.png)
Wektor dołączony (3)
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & -1 & 1 \\ -1 & -1 & 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \\ t \\ s \end{bmatrix} = \begin{bmatrix} \delta \\ -\varphi+\beta \\ \epsilon \\ \gamma + \beta + \delta \\ \varphi \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-56d1bf0a6859fe2e70eda90e108ea675_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} {\R{0 = \delta }} \\ -y-t+s=-\varphi+\beta \quad \Rightarrow \ s=\beta \\ -x-y+w-t+s = \epsilon \quad \Rightarrow \ w=\epsilon + \varphi -\beta + x \\ {\R{0 = \gamma + \beta + \delta}} \quad {\R{\Rightarrow \gamma = -\beta}} \\ y+t = \varphi \quad \Rightarrow \ y=-t + \varphi \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6bf4db8e9756962fc50d2f8689e64831_l3.png)
Wektory dołączone (3)
![Rendered by QuickLaTeX.com \[\begin{cases} {\R{0 = \delta }} \\ s = \beta \\ w = \epsilon+\varphi-\beta+x \\ {\R{\gamma = -\beta}} \\ y = -t+\varphi \end{cases} \Rightarrow \begin{bmatrix} \eta \\ -\kappa+\varphi \\ \theta \\ \epsilon +\varphi- \beta + \eta \\ \kappa \\ \beta \end{bmatrix}, \mbox{ gdzie } {\R{0}}^2+{\R{2}}\beta^2 +>0\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3de226ce4649a6ce17cc3e3edf903247_l3.png)
Wektory dołączone (4){\R{?}}
![Rendered by QuickLaTeX.com \[\begin{cases} s = \varphi \\ w = \theta+\kappa - \varphi+x \\ y = -t+\kappa \end{cases} \Rightarrow \begin{bmatrix} \psi \\ -\pi+\kappa \\ \Omega \\ \theta +\kappa - \varphi + \psi \\ \pi \\ \varphi \end{bmatrix}, \mbox{ gdzie } \alpha^2+\beta^2 +\gamma^2>0\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-db383c06fcae81ada69de6f4bb64c943_l3.png)
- Tu już nie ma, ani
 , ani
, ani  , ani
, ani  , które były w wektorze własnym.
, które były w wektorze własnym.
Podsumowanie
![Rendered by QuickLaTeX.com \[\hspace{-0.3cm} \begin{bmatrix} {\ZLO{\alpha}} \\ -{\ZLO{\beta}} \\ {\ZLO{\gamma}} \\ {\ZLO{\alpha}} \\ {\ZLO{\beta}} \\ 0 \end{bmatrix} \to \begin{bmatrix} \delta \\ -\varphi+{\ZLO{\beta}} \\ \epsilon \\ {\ZLO{\gamma}} + {\ZLO{\beta}} + \delta \\ \varphi \\ 0 \end{bmatrix}_{\begin{tiny} \begin{matrix} \alpha = 0 \end{matrix} \end{tiny}} \to \begin{bmatrix} \eta \\ -\kappa+\varphi \\ \theta \\ \epsilon +\varphi- {\ZLO{\beta}} + \eta \\ \kappa \\ {\ZLO{\beta}} \end{bmatrix}_{\begin{tiny} \begin{matrix} \alpha = 0 \\ \delta = 0 \\ \gamma = -\beta \end{matrix} \end{tiny}} {\G{\to \begin{bmatrix} \psi \\ -\pi+\kappa \\ \Omega \\ \theta +\kappa - \varphi + \psi \\ \pi \\ \varphi \end{bmatrix}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0fcb34647d6f129275d34c11d980821b_l3.png)
- Pierwszy zależy od
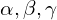
- Drugi zależy od
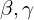 oraz
oraz 
- Trzeci zależy od
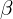 oraz
oraz 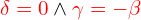
- Mamy klatkę stopnia 1, stopnia 2 i stopnia 3
Wybór wektorów do macierzy przejścia
-
- Wektor dla klatki stopnia
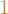 to np.
to np.
- Wektor dla klatki stopnia
![Rendered by QuickLaTeX.com \[{\ZLO{\begin{cases} \alpha = 1 \\ \beta = \gamma = \delta= \varphi = \epsilon = \eta = \kappa = \theta = \psi = \pi = \Omega = 0 \end{cases}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-759928f1af15e738dc024ed89b9035e4_l3.png)
-
- Wektory dla klatki stopnia
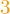 to np.
to np.
- Wektory dla klatki stopnia
![Rendered by QuickLaTeX.com \[{\Y{\begin{cases} \beta = 1 \\ \gamma = -1 \\ \alpha = \delta= \varphi = \epsilon = \eta = \kappa = \theta = \psi = \pi = \Omega = 0 \end{cases}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-86ccaee33a45ad2f9b1173c3698527b0_l3.png)
-
- Wektory dla klatki stopnia
 to np.
to np.
- Wektory dla klatki stopnia
![Rendered by QuickLaTeX.com \[{\W{\begin{cases} \gamma = 1 \\ \alpha = \beta = \delta= \varphi = \epsilon = \eta = \kappa = \theta = \psi = \pi = \Omega = 0 \end{cases}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-5b33795fde8189219a0593c5031bb881_l3.png)
Macierz przejścia – zmiany bazy
![Rendered by QuickLaTeX.com \[\hspace{-0.7cm} \M{W} = \begin{bmatrix} {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{1}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{0}} & {\Y{0}} & {\W{1}} & {\W{0}} \\ {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{-1}} & {\W{0}} & {\W{1}} \\ {\ZLO{0}} & {\Y{1}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{0}} & {\Y{0}} & {\Y{1}} & {\W{0}} & {\W{0}} \\ \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-60151e3a10ec2c3d6ccf5522ac2c4a25_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{-0.7cm}\begin{bmatrix} {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{1}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{0}} & {\Y{0}} & {\W{1}} & {\W{0}} \\ {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{-1}} & {\W{0}} & {\W{1}} \\ {\ZLO{0}} & {\Y{1}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{0}} & {\Y{0}} & {\Y{1}} & {\W{0}} & {\W{0}} \\ \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{1}} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\Y{1}} & {\Y{1}} & {\Y{0}} & 0 & 0 \\ 0 & {\Y{0}} & {\Y{1}} & {\Y{1}} & 0 & 0 \\ 0 & {\Y{0}} & {\Y{0}} & {\Y{1}} & 0 & 0\\ 0 & 0 & 0 & 0 & {\W{1}} & {\W{1}} \\ 0 & 0 & 0 & 0 & {\W{0}} & {\W{1}} \\ \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{1}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{0}} & {\Y{0}} & {\W{1}} & {\W{0}} \\ {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{-1}} & {\W{0}} & {\W{1}} \\ {\ZLO{0}} & {\Y{1}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{0}} & {\Y{0}} & {\Y{1}} & {\W{0}} & {\W{0}} \\ \end{bmatrix}^{-1}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-831da97b2ca54f22b287ce725ad60067_l3.png)
![Rendered by QuickLaTeX.com \[=\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 1 \\ -1 & -1 & 1 & 1 & -1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c5798c0156c2c4fb89f60baadd9a38fd_l3.png)
Sposób 2 (szybszy)
-
- Kolejne potęgi macierzy
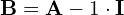
- Kolejne potęgi macierzy
![Rendered by QuickLaTeX.com \[\hspace{-1cm} \M{B} = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & -1 & 1 \\ -1 & -1 & 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \qquad \qquad \M{B}^2 =\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-128c9a350520d703fd19366929cc3c86_l3.png)
Poprzednie wektory dołączone
-
- Ten wektor to np.
![Rendered by QuickLaTeX.com \[\M{u}^{3} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3fbbbc419148687aa46a1903b1c48663_l3.png)
- Wówczas obliczamy kolejne coraz niższego rzędu wektory dołączone, tzn.
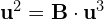
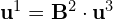
![Rendered by QuickLaTeX.com \[\M{u}^{2}= \M{B} \cdot \M{u}^3 =\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & -1 & 1 \\ -1 & -1 & 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}\cdot \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a61f782daf3af6b99095135025bc082f_l3.png)
![Rendered by QuickLaTeX.com \[\M{u}^{1}= \M{B}^2 \cdot \M{u}^3 = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ -1 \\ -1 \\ 0 \\ 1 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-286011acec6f33b029df2a7059ea80e0_l3.png)
Skąd wiadomo w takim razie jakie będą klatki Jordana
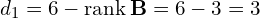
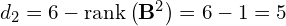
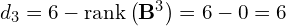
- Jak nam wyszło 6 to następne wiadomo, że będzie
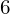
- Klatek będzie

- Klatek stopnia większego od 1 będzie
- Klatek stopnia większego od 2 będzie
- Klatek stopnia większego od 3 będzie
Mamy wektory tylko dla klatki stopnia 3
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & {{0}} & 0 \\ -1 & {{1}} & 0 \\ -1 & {{1}} & 0 \\ 0 & {{0}} & 0 \\ 1 & {{0}} & 0 \\ 0 & {{0}} & 1 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bd505c700fc04d79328e089cd05dc348_l3.png)
-
- Teraz wybieramy wektor dołączony rzędu 2 dla klatki stopnia 2, ale niezależny liniowo już z tymi co zostały użyte w znalezionej klatce.
- Może być to np.
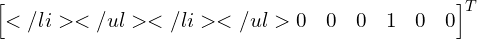
Dla klatki stopnia 2

-
- Oczywiście nie jest on także wektorem własnym, ale jest, taki że
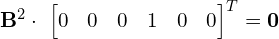
-
- Wektor własny dla tego wektora to
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 & -1 & 1 \\ -1 & -1 & 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}\cdot \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f1b047d102532e26e0fd783ad9a23c56_l3.png)
Teraz mamy już wektory dla dwóch klatek
![Rendered by QuickLaTeX.com \[\begin{bmatrix} {\Y{0}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\Y{-1}} & {\Y{1}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\Y{-1}} & {\Y{1}} & {\Y{0}} & {\W{1}} & {\W{0}} \\ {\Y{0}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{1}} \\ {\Y{1}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\Y{0}} & {\Y{0}} & {\Y{1}} & {\W{0}} & {\W{0}} \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9b3991b349d7f7e598d989e9d00b938b_l3.png)
- Pozostało wybrać wektor własny dla trzeciej klatki Jordana stopnia 1, który będzie niezależny liniowo z już wybranymi.
- Może to być np.
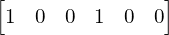
![Rendered by QuickLaTeX.com \[\hspace{-0.7cm}\begin{bmatrix} {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{1}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\R{1}} & {\Y{0}} & {\W{1}} & {\W{0}} \\ {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\R{0}} & {\W{0}} & {\W{1}} \\ {\ZLO{0}} & {\Y{1}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{0}} & {\Y{0}} & {\Y{1}} & {\W{0}} & {\W{0}} \\ \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{1}} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\Y{1}} & {\Y{1}} & {\Y{0}} & 0 & 0 \\ 0 & {\Y{0}} & {\Y{1}} & {\Y{1}} & 0 & 0 \\ 0 & {\Y{0}} & {\Y{0}} & {\Y{1}} & 0 & 0\\ 0 & 0 & 0 & 0 & {\W{1}} & {\W{1}} \\ 0 & 0 & 0 & 0 & {\W{0}} & {\W{1}} \\ \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\Y{1}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{-1}} & {\R{1}} & {\Y{0}} & {\W{1}} & {\W{0}} \\ {\ZLO{1}} & {\Y{0}} & {\Y{0}} & {\R{0}} & {\W{0}} & {\W{1}} \\ {\ZLO{0}} & {\Y{1}} & {\Y{0}} & {\Y{0}} & {\W{0}} & {\W{0}} \\ {\ZLO{0}} & {\Y{0}} & {\Y{0}} & {\Y{1}} & {\W{0}} & {\W{0}} \\ \end{bmatrix}^{-1}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-154a904beea07e7978fd0b59bd6c97dd_l3.png)
![Rendered by QuickLaTeX.com \[=\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -1 & 1 \\ -1 & -1 & 1 & 1 & -1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c5798c0156c2c4fb89f60baadd9a38fd_l3.png)
Oczywiście wpasowuje się to w nasz wcześniej wyznaczony model tzn.
![Rendered by QuickLaTeX.com \[\hspace{-0.3cm} \begin{bmatrix} {\ZLO{\alpha}} \\ -{\ZLO{\beta}} \\ {\ZLO{\gamma}} \\ {\ZLO{\alpha}} \\ {\ZLO{\beta}} \\ 0 \end{bmatrix} \to \begin{bmatrix} \delta \\ -\varphi+{\ZLO{\beta}} \\ \epsilon \\ {\ZLO{\gamma}} + {\ZLO{\beta}} + \delta \\ \varphi \\ 0 \end{bmatrix}_{\begin{tiny} \begin{matrix} \alpha = 0 \end{matrix} \end{tiny}} \to \begin{bmatrix} \eta \\ -\kappa+\varphi \\ \theta \\ \epsilon +\varphi- {\ZLO{\beta}} + \eta \\ \kappa \\ {\ZLO{\beta}} \end{bmatrix}_{\begin{tiny} \begin{matrix} \alpha = 0 \\ \delta = 0 \\ \gamma = -\beta \end{matrix} \end{tiny}} {\G{\to \begin{bmatrix} \psi \\ -\pi+\kappa \\ \Omega \\ \theta +\kappa - \varphi + \psi \\ \pi \\ \varphi \end{bmatrix}}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0fcb34647d6f129275d34c11d980821b_l3.png)
- klatka st. 1 to
 ,
, 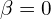 ,
, 
- klatka st. 3 to
 ,
,  ,
, 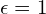 , reszta to 0
, reszta to 0 - klatka st. 2 to
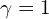 reszta to 0
reszta to 0
Przykład 10 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\M{A} = \begin{bmatrix} 2 & -1 \\ 3 & 2 \\ \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1e41782dd050866f505eae04d72f1302_l3.png)
![Rendered by QuickLaTeX.com \[\det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 2-\lambda & -1 \\ 3 & -\sqrt{3}i \\ \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b809c30f0fd1f4d8ec842f3f347401dc_l3.png)
![Rendered by QuickLaTeX.com \[= (2-\lambda)^2+3= 4- 4\lambda +\lambda^2+3=\lambda^2-4\lambda+7\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-cb796c488e9d3d2ad08001de3aa61901_l3.png)
Przykład 10 wartości własne i wektory własne
-
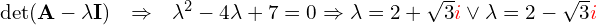
- dla
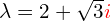
![Rendered by QuickLaTeX.com \[\hspace{-1.52cm}\begin{bmatrix} 2 & -1 \\ 3 & 2 \\ \end{bmatrix} \qquad (\M{A}-(2+\sqrt{3}i)\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} -\sqrt{3}i & -1 \\ 3 & -\sqrt{3}i \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6140db3f63dfb32c6139062d26b5edee_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{-1.5cm} \begin{cases} -\sqrt{3}ix -y = 0 \\ 3x-\sqrt{3}iy = 0 \end{cases} \Rightarrow x = \frac{\sqrt{3}}{3}iy\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-be7cfc990b86b503afc083b06bb62d5f_l3.png)
Przykład 10 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[x = \frac{\sqrt{3}}{3}iy \qquad \Rightarrow \qquad \begin{bmatrix} \frac{\sqrt{3}}{3}i\alpha \\ \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-84eabafe9de331ddb68382dce1a72cd3_l3.png)
- Będzie 1 klatka stopnia 1
Przykład 10 wartości własne i wektory własne
-
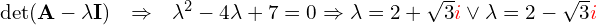
- dla
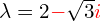
![Rendered by QuickLaTeX.com \[\hspace{-1.52cm}\begin{bmatrix} 2 & -1 \\ 3 & 2 \\ \end{bmatrix} \qquad (\M{A}-(2{\R{-}}\sqrt{3}i)\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} \sqrt{3}i & -1 \\ 3 & \sqrt{3}i \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e568538294d644689fed3e245c3bbd33_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{-1.5cm} \begin{cases} \sqrt{3}ix -y = 0 \\ 3x+\sqrt{3}iy = 0 \end{cases} \Rightarrow x = {\R{-}}\frac{\sqrt{3}}{3}iy\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b6bc02937748aebecf8743461218aaed_l3.png)
Przykład 10 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[x = -\frac{\sqrt{3}}{3}iy \qquad \Rightarrow \qquad \begin{bmatrix} -\frac{\sqrt{3}}{3}i\alpha \\ \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d709f2ac245de7fcc1965920275310b8_l3.png)
- Będą 1 klatki stopnia 1
Rozkład macierz w postaci Jordana
-
- Wektory własne to
![Rendered by QuickLaTeX.com \[\begin{bmatrix} +\frac{\sqrt{3}}{3}i\alpha \\ \alpha \end{bmatrix} \qquad \qquad \begin{bmatrix} -\frac{\sqrt{3}}{3}i\alpha \\ \alpha \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-910e6c544f63fd0b8f5601ce7da0ee49_l3.png)
-
- Powstały rozkład dla
- Powstały rozkład dla
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 2 & -1 \\ 3 & 2 \end{bmatrix} = \begin{bmatrix} {\ZLO{\frac{\sqrt{3}}{3}{\R{i}}}} & {\W{-\frac{\sqrt{3}}{3}{\R{i}} }}\\ {\ZLO{1}} & {\W{1}} \\ \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{2+\sqrt{3}{\R{i}}}} & 0 \\ 0 & {\W{2-\sqrt{3}{\R{i}}}} \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{\frac{\sqrt{3}}{3}{\R{i}}}} & {\W{-\frac{\sqrt{3}}{3}{\R{i}} }}\\ {\ZLO{1}} & {\W{1}} \\ \end{bmatrix}^{-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c1d0137be1556331b809f79db1fb6345_l3.png)
Rozkład macierz w postaci Jordana baza rzeczywistych
-
- Wektory własne to
![Rendered by QuickLaTeX.com \[\hspace{-1.0cm}\begin{bmatrix} \frac{\sqrt{3}}{3}i\alpha \\ \alpha \end{bmatrix} =\begin{bmatrix} 0 \\ \alpha \end{bmatrix} +i\begin{bmatrix} +\frac{\sqrt{3}}{3}\alpha \\ 0 \end{bmatrix} \qquad \qquad \begin{bmatrix} -\frac{\sqrt{3}}{3}i\alpha \\ \alpha \end{bmatrix} =\begin{bmatrix} 0 \\ \alpha \end{bmatrix} +i\begin{bmatrix} -\frac{\sqrt{3}}{3}\alpha \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-86c647269f25fbd911f0f075811d9563_l3.png)
-
- Można też tak jak ktoś nie che mieć liczb zespolonych w rozkładzie
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 2 & -1 \\ 3 & 2 \end{bmatrix} = \begin{bmatrix} 0 & \frac{\sqrt{3}}{3} \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & \sqrt{3} \\ -\sqrt{3} & 2 \end{bmatrix} \cdot \begin{bmatrix} 0 & \frac{\sqrt{3}}{3} \\ 1 & 0 \\ \end{bmatrix}^{-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6a377778dbc35332ce47b1db1d221a19_l3.png)
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 2 & -1 \\ 3 & 2 \end{bmatrix} = \begin{bmatrix} 0 & -\frac{\sqrt{3}}{3} \\ 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 & -\sqrt{3} \\ \sqrt{3} & 2 \end{bmatrix} \cdot \begin{bmatrix} 0 & -\frac{\sqrt{3}}{3} \\ 1 & 0 \\ \end{bmatrix}^{-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f23fd60597779f09a07d13c7bc23b5b9_l3.png)
Przykład 11 wielomian charakterystyczny
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 2 & 0 & 3 & 0 \\ 1 & 2 & 0 & 3 \\ -3 & 0 & 2 & 0 \\ 0 & -3 & 1 & 2 \end{bmatrix} \qquad \det(\M{A}-\lambda\M{I}) = \begin{vmatrix} 2-\lambda & 0 & 3 & 0 \\ 1 & 2-\lambda & 0 & 3 \\ -3 & 0 & 2-\lambda & 0 \\ 0 & -3 & 1 & 2-\lambda \end{vmatrix}=\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1fd0e51fb74b1e082b2a292e0e1502d4_l3.png)
![Rendered by QuickLaTeX.com \[= (2-\lambda)\begin{vmatrix} 2-\lambda & 0 & 3 \\ 0 & 2-\lambda & 0 \\ -3 & 1 & 2-\lambda \\ \end{vmatrix} + 3 \begin{vmatrix} 1 & 2-\lambda & 3 \\ -3 & 0 & 0 \\ 0 & -3 & 2-\lambda \\ \end{vmatrix} =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a9ce5f32c945e70377e004cf2ebd8d51_l3.png)
![Rendered by QuickLaTeX.com \[=(2-\lambda)^4+9(2-\lambda)^2 + 81 + 9(2-\lambda)^2 =\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-62a618e94184459631f00427c58fe1fc_l3.png)
![Rendered by QuickLaTeX.com \[=(2-\lambda)^2\left((2-\lambda)^2+9\right)+ 9\left((2-\lambda)^2+9\right)= \left((2-\lambda)^2+9\right)^2\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2a0dcd12d6bcf4dd05bad151ca24224f_l3.png)
Przykład 11 wartości własne i wektory własne
-
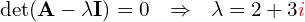 krotność algebraiczna 2 oraz
krotność algebraiczna 2 oraz 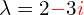 też z krotnością algebraiczną 2
też z krotnością algebraiczną 2- dla
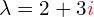
![Rendered by QuickLaTeX.com \[\hspace{-1.52cm}\begin{bmatrix} 2 & 0 & 3 & 0 \\ 1 & 2 & 0 & 3 \\ -3 & 0 & 2 & 0 \\ 0 & -3 & 1 & 2 \end{bmatrix} \qquad (\M{A}-(2+3{\R{i}})\cdot \M{I})\M{v} = 0 \ \Rightarrow \ \begin{bmatrix} -3i & 0 & 3 & 0 \\ 1 & -3i & 0 & 3 \\ -3 & 0 & -3i & 0 \\ 0 & -3 & 1 & -3i \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\0 \\ 0 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-cf96d5020b75cf452e680747836e4851_l3.png)
![Rendered by QuickLaTeX.com \[\hspace{-1.5cm} \begin{cases} -3ix+3z=0 \\ x -3iy+3w=0 \\ -3x-3iz = 0 \\ -3y+z -3iw =0 \\ \end{cases} \Rightarrow \begin{cases} z = ix \\ x = 3iy-3w \\ ix - 3y -3iw = 0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-381f7640437c3e83bc267c80a0770734_l3.png)
Przykład 11 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{cases} z = ix \\ x = 3iy-3w \\ ix - 3y -3iw = 0 \end{cases} \Rightarrow \begin{cases} z = ix \\ x = 3iy-3w \\ -3y -3iw-3y-3iw=0 \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8500a0cdd98e3ca9ba0b9b544ad9721e_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} z= ix \\ x = 0 \\ w = yi \end{cases} \qquad \begin{bmatrix} 0 \\ \alpha \\ 0\\ \alpha i \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-59b05bbabfd859c218c49f4cd5c6bd60_l3.png)
- Będzie 1 klatka stopnia 2
Przykład 11 – Wektor dołączony
![Rendered by QuickLaTeX.com \[\begin{bmatrix} -3i & 0 & 3 & 0 \\ 1 & -3i & 0 & 3 \\ -3 & 0 & -3i & 0 \\ 0 & -3 & 1 & -3i \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix} 0 \\ \alpha \\ 0\\ \alpha i \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6a51ce73da5b62c4d828c21398d2c0a9_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} -3ix+3z=0 \\ x -3iy+3w=\alpha \\ -3x-3iz = 0 \\ -3y+z -3iw =\alpha i \\ \end{cases} \Rightarrow \begin{cases} z = ix \\ x = 3iy-3w+\alpha\\ -3y+ix-3iw=\alpha i \end{cases} \Rightarrow\begin{cases} z = ix \\ w = y i \\ x = \alpha \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f447d38c68cee53776161e67cfe8f823_l3.png)
Przykład 11 – Wektor własny
-
- Wektor własny jest postaci
![Rendered by QuickLaTeX.com \[\begin{cases} z = ix \\ w = y i \\ x = \alpha \end{cases} \qquad \Rightarrow \qquad \begin{bmatrix} \alpha \\ \beta \\ \alpha i \\ \beta i \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c4c18af78bcdc3483028f0a7b924d6f9_l3.png)
- Będzie 1 klatka stopnia 2
Rozkład macierz w postaci Jordana
-
- Łańcuchy Jordana to:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 \\ \alpha \\ 0 \\ \alpha i \end{bmatrix} \to \begin{bmatrix} \alpha \\ \beta \\ \alpha i \\ \beta i \end{bmatrix} \qquad \qquad \begin{bmatrix} 0 \\ \alpha \\ 0 \\ -\alpha i \end{bmatrix} \to \begin{bmatrix} \alpha \\ \beta \\ -\alpha i \\ -\beta i \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-37f1495aade4e72f473eff970e977e08_l3.png)
-
- Powstały rozkład dla
- Powstały rozkład dla
![Rendered by QuickLaTeX.com \[\hspace{-1.5cm}\begin{bmatrix} {\ZLO{0}} & {\ZLO{1}} & {\W{0}} & {\W{1}} \\ {\ZLO{1}} & {\ZLO{0}} & {\W{1}} & {\W{0}} \\ {\ZLO{0}} & {\ZLO{i}} & {\W{0}} & {\W{-i}} \\ {\ZLO{i}} & {\ZLO{0}} & {\W{-i}} & {\W{0}} \\ \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{2+3i}} & {\ZLO{1}} & 0 & 0 \\ {\ZLO{0}} & {\ZLO{2+3i}} & 0 & 0 \\ 0 & 0 & {\W{2-3i}} & {\W{1}} \\ 0 & 0 & {\W{0}} & {\W{2-3i}} \\ \end{bmatrix} \cdot \begin{bmatrix} {\ZLO{0}} & {\ZLO{1}} & {\W{0}} & {\W{1}} \\ {\ZLO{1}} & {\ZLO{0}} & {\W{1}} & {\W{0}} \\ {\ZLO{0}} & {\ZLO{i}} & {\W{0}} & {\W{-i}} \\ {\ZLO{i}} & {\ZLO{0}} & {\W{-i}} & {\W{0}} \\ \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e7277eed391c325a25256e2444a34510_l3.png)
Rozkład macierz w postaci Jordana baza rzeczywistych
-
- Łańcuch Jordana
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 \\ \alpha \\ 0 \\ \alpha i \end{bmatrix}=\begin{bmatrix} 0 \\ \alpha \\ 0 \\ 0 \end{bmatrix}+{\R{i}}\begin{bmatrix} 0 \\ 0 \\ 0 \\ \alpha \end{bmatrix} \qquad \to \qquad \begin{bmatrix} \alpha \\ \beta \\ \alpha i \\ \beta i \end{bmatrix}=\begin{bmatrix} \alpha \\ \beta \\ 0 \\ 0 \end{bmatrix}+{\R{i}}\begin{bmatrix} 0 \\ 0 \\ \alpha \\ \beta \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-73edf1a9fa287b7c8e80718665424a28_l3.png)
-
- Można też tak jak ktoś nie che mieć liczb zespolonych w rozkładzie
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} 2 & 3 & {\R{1}} & 0 \\ -3 & 2 & 0 & {\R{1}} \\ 0 & 0 & 2 & 3 \\ 0 & 0 & -3 & 2 \\ \end{bmatrix} \cdot \begin{bmatrix} 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{bmatrix}^{-1} = \M{A}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4eca972f52aa481974f6a943173207a5_l3.png)
Rozkład Jordana
-
- Na pierwszy rzut oka wygląda bardzo podobnie
![Rendered by QuickLaTeX.com \[\M{A} = \M{W} \M{J} \M{W}^{-1},\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2ced6ac72c8906e577129c4440364e5a_l3.png)
![Rendered by QuickLaTeX.com \[\M{J} = \begin{bmatrix} \M{K}_1 & \M{0} & \cdots & \M{0} \\ \M{0} & \M{K}_2 & \cdots & \M{0} \\ \vdots & \vdots & \vdots & \vdots \\ \M{0} & \M{0} & \cdots & \M{K}_{\R{q}} \\ \end{bmatrix} \qquad \M{K}_{\R{i}} = \begin{bmatrix} \lambda_{\R{i}} & 1 & 0 & \cdots & 0 \\ 0 & \lambda_{\R{i}} & 1 & \cdots & 0 \\ 0 & 0 & \lambda_{\R{i}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \lambda_{\R{i}} \\ \end{bmatrix},\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-497bec840b63837d24f9bdc47030d974_l3.png)
gdzie
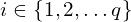 ,
,- Jednak teraz Macierz
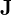 nie jest diagonalna.
nie jest diagonalna. - Macierz
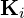 są nazywane klatkami i są różnych stopni.
są nazywane klatkami i są różnych stopni.
NAJWAŻNIEJSZE
-
- Każdą macierz
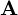 można zapisać w postaci Jordana.
można zapisać w postaci Jordana.
- Każdą macierz
![Rendered by QuickLaTeX.com \[\M{A} = \M{W} \cdot \M{J} \cdot \M{W}^{-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-889c59d264426cf1eb64933bc9f10c5d_l3.png)
- Macierz Jordana
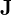 jest wyznacza jednoznacznie z dokładnością do ewentualnego przestawiania kolejności klatek Jordana.
jest wyznacza jednoznacznie z dokładnością do ewentualnego przestawiania kolejności klatek Jordana. - Nie ma zatem możliwości, aby dla tej samej macierzy
 istniały dwie różne macierze Jordana
istniały dwie różne macierze Jordana  , które będą miały inną liczbę i rodzaj klatek.
, które będą miały inną liczbę i rodzaj klatek. 
- Natomiast macierz przejścia
 jest wyznaczana niejednoznacznie, jest ich nieskończenie wiele do wyboru.
jest wyznaczana niejednoznacznie, jest ich nieskończenie wiele do wyboru. 






NAJWAŻNIEJSZE
- Macierz
 różnie jest nazywana: macierz zmiany bazy, macierz modalna, macierz podobieństwa, macierz ustalająca podobieństwo
różnie jest nazywana: macierz zmiany bazy, macierz modalna, macierz podobieństwa, macierz ustalająca podobieństwo - Macierz
 składa się z wektorów własnych liniowo niezależnych i wówczas rozkład Jordana sprowadza się do diagonalizacji macierzy.
składa się z wektorów własnych liniowo niezależnych i wówczas rozkład Jordana sprowadza się do diagonalizacji macierzy. - Natomiast jeżeli liczba wektorów własnych liniowo niezależnych jest mniejsza od
 (stopień macierz
(stopień macierz  ), to wówczas trzeba umiejętnie wyszukać wektory dołączone.
), to wówczas trzeba umiejętnie wyszukać wektory dołączone. - Następnie te wektory trzeba umiejętnie dołożyć do wektorów własnych aby zbudować macierz
Procedura
-
- Dana jest dowolna macierz
 o stopniu
o stopniu 
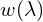 wielomian charakterystyczny macierzy
wielomian charakterystyczny macierzy  powstały z
powstały z
- Dana jest dowolna macierz
![Rendered by QuickLaTeX.com \[\det \left( \M{A} -\lambda\M{I} \right) \qquad \Rightarrow \qquad w(\lambda)\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b694e53b4798a7ce68d4f526ed836529_l3.png)
-
- Rozwiązanie równania charakterystycznego
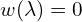 są wartości własne
są wartości własne 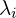 – wartość własna, dla
– wartość własna, dla 
- przy czym mamy
 , gdy
, gdy 
 liczba różnych wartości własnych
liczba różnych wartości własnych – krotność algebraiczna
– krotność algebraiczna 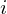 -tej wartości własnej
-tej wartości własnej 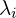
- zawsze jest spełnione
- Rozwiązanie równania charakterystycznego
![Rendered by QuickLaTeX.com \[k_1+k_2+k_3 + \ldots + k_r = n\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-76067b6e28caa00adc5de27022018ff5_l3.png)
Procedura
-
- Dla każdej z kolejnych wartości własnych
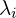 , gdzie
, gdzie  przeprowadzamy szereg czynności
przeprowadzamy szereg czynności
- Wyznaczamy przestrzeń własną
- Dla każdej z kolejnych wartości własnych
![Rendered by QuickLaTeX.com \[\ker \left( \M{A}-\lambda_i\M{I} \right)\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-19f48c7d04f223f5cef026344765b16d_l3.png)
-
-
- Wymiar przestrzeni własnej.
-
![Rendered by QuickLaTeX.com \[\dim \left( \ker \left( \M{A}-\lambda_i\M{I} \right)\right) \quad = \quad d_1 \quad = \quad n-\rank (\M{A}-\lambda_i\M{I})\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-948149385d9d428091f3dea8f8bd6ed8_l3.png)
-
- Jeżeli
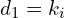 , to wybieramy dowolne
, to wybieramy dowolne 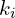 wektorów niezależnych liniowo
wektorów niezależnych liniowo - Natomiast jeżeli
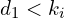 , to
, to
- Jeżeli
Procedura
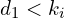 < strong=””></k_i
< strong=””></k_i d_1 < k_i
d_1 < k_i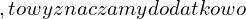 k_i – d_1
k_i – d_1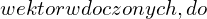 d_1
d_1 d_1
d_1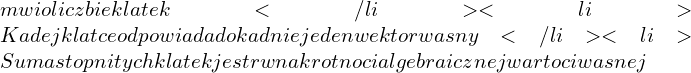 \lambda_i
\lambda_i![Rendered by QuickLaTeX.com </li> </ul> </li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ad92d8e8114e8d01c4ab4b30629e03f5_l3.png" height="20" width="210" class="ql-img-displayed-equation " alt="\[s_1+s_2+\ldots+ s_{d_1} = k_i\]" title="Rendered by QuickLaTeX.com"/> <ul> <li style="list-style-type: none;"> <ul> <li style="list-style-type: none;"> <ul> <li>Dla łatwiejszego opisu dalszej teorii przyjmijmy, że są w kolejności nierosnącej</li> </ul> </li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-60d1262488c82dcfba5fb54ee06ece4d_l3.png" height="19" width="217" class="ql-img-displayed-equation " alt="\[m = s_1\geq s_2 \geq \ldots \geq s_{d_1}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li style="list-style-type: none;"> <ul> <li>Identyfikujemy stopnie klatek Jordana</li> </ul> </li> </ul> <strong>Algorytmiczne wyznaczanie liczby i rodzaju klatek</strong> <ul> <li style="list-style-type: none;"> <ul> <li>Obliczamy wymiar jądra kolejnych potęg](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ec0c22c4c655623ffa5473e0363e5e65_l3.png)
(\M{A}-\lambda_i\M{I})
 d_1 = \dim \ker \left( (\M{A}-\lambda_i\M{I})\right)
d_1 = \dim \ker \left( (\M{A}-\lambda_i\M{I})\right) d_2 = \dim \ker \left( (\M{A}-\lambda_i\M{I})^2\right)
d_2 = \dim \ker \left( (\M{A}-\lambda_i\M{I})^2\right) d_3 = \dim \ker \left( (\M{A}-\lambda_i\M{I})^3\right)
d_3 = \dim \ker \left( (\M{A}-\lambda_i\M{I})^3\right) \vdots
\vdots d_1 = n-\rank (\M{A}-\lambda_i\M{I})
d_1 = n-\rank (\M{A}-\lambda_i\M{I}) d_2 = n-\rank \left( (\M{A}-\lambda_i\M{I})^2\right)
d_2 = n-\rank \left( (\M{A}-\lambda_i\M{I})^2\right) d_3 = n-\rank \left( (\M{A}-\lambda_i\M{I})^3\right)
d_3 = n-\rank \left( (\M{A}-\lambda_i\M{I})^3\right) \vdots
\vdots![Rendered by QuickLaTeX.com </li> </ul> </li> <li>Wynika to z twierdzenia Sylvestra</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-182e3b7a93bb10834b0ac7029a5b2071_l3.png" height="22" width="314" class="ql-img-displayed-equation " alt="\[\dim \ker \left( \M{B} \right) + \dim \im \left(\M{B} \right) = \dim V\]" title="Rendered by QuickLaTeX.com"/> <strong>Algorytmiczne wyznaczanie liczby i rodzaju klatek</strong> <ul> <li>Wówczas <ul> <li>](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-79e9e3cc019c92cb6dc41fa990e0d762_l3.png)
d_1
 d_2-d_1
d_2-d_1 d_3-d_2
d_3-d_2 \vdots
\vdots m
m d_m
d_m d_{m}-d_{m-1}\neq0
d_{m}-d_{m-1}\neq0 d_{m+1}-d_{m}=0
d_{m+1}-d_{m}=0 m = s_1
m = s_1 d_{m-1}=d_{m}=d_{m+1}=\ldots=0
d_{m-1}=d_{m}=d_{m+1}=\ldots=0 d_{m-1}=d_{m}=d_{m+1}=\ldots=2
d_{m-1}=d_{m}=d_{m+1}=\ldots=2 s_1, s_2, \ldots, s_{d_1}
s_1, s_2, \ldots, s_{d_1} \lambda_i
\lambda_i \M{J}
\M{J} \lambda_i
\lambda_i \M{J}_i
\M{J}_i![Rendered by QuickLaTeX.com </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b7a977fe2f639dc6239a0123bc520e3e_l3.png" height="451" width="724" class="ql-img-displayed-equation " alt="\[\hspace{-0.5cm}\M{J} = \begin{bmatrix} \ddots & \vdots & \vdots & \vdots & \vdots & \\ \ldots & \begin{bmatrix} \lambda_i & 1 & \ldots & 0 \\ 0 & \lambda_i & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \lambda_i \end{bmatrix} & & & & \ldots \\ \ldots & & \begin{bmatrix} \lambda_i & 1 & \ldots & 0 \\ 0 & \lambda_i & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \lambda_i \end{bmatrix} & & & \ldots \\ \ldots & & & \ddots & & \ldots \\ \ldots & & & & \begin{bmatrix} \lambda_i & 1 & \ldots & 0 \\ 0 & \lambda_i & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \lambda_i \end{bmatrix} & \ldots \\ & \vdots & \vdots & \vdots & \vdots & \ddots \\ \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4d2e5ca21366d912e39868d21ec3cd45_l3.png)
i
 \M{W}
\M{W} s_1
s_1 \M{W}_{i,1}
\M{W}_{i,1} [n\times s_1]
[n\times s_1] s_2
s_2 \M{W}_{i,2}
\M{W}_{i,2} [n\times s_2]
[n\times s_2] \M{W}_{i,d_i}
\M{W}_{i,d_i} [n\times s_{d_1}]
[n\times s_{d_1}] [n\times k_i]
[n\times k_i] r
r![Rendered by QuickLaTeX.com </li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-01408415d68e9c7caa8939ca8301367c_l3.png" height="82" width="303" class="ql-img-displayed-equation " alt="\[\M{W}_i = \begin{bmatrix} & & & \\ \M{W}_{i,1} & \M{W}_{i,2} & \ldots & \M{W}_{i,d_1} \\ & & & \\ \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>Wyliczanie wektorów dołączonych dla](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-be006a19ef0859d2eef504f30955e719_l3.png)
\M{W}_i
 \M{v}_i
\M{v}_i m
m*** QuickLaTeX cannot compile formula: .</li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9fb0e92389dca630ee0446940583ad35_l3.png" height="168" width="482" class="ql-img-displayed-equation " alt="\[\hspace{-0.5cm}\begin{matrix} 1) \quad & \left( \M{A}-\lambda_i \M{I} \right) \M{v}_i=\M{0} & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{} \M{v}_i=\M{0} \\ % & \qquad \\ 2) \quad & \left( \M{A}-\lambda_i \M{I} \right) \M{u}_i^{2}=\M{v}_i & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{2} \M{u}_i^{2}=\M{0} \\ % & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{s_m-1} \M{u}_i^{s_m}=\M{v}_i \\ 3) \quad & \left( \M{A}-\lambda_i \M{I} \right) \M{u}_i^{3}=\M{u}_i^{2} & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{3} \M{u}_i^{3}=\M{0} \\ % & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{s_m-2} \M{u}_i^{s_m-1}=\M{v}_i \\ 4) \quad & \left( \M{A}-\lambda_i \M{I} \right) \M{u}_i^{4}=\M{u}_i^{3} & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{4} \M{u}_i^{4}=\M{0} \\ % & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{s_m-3} \M{u}_i^{s_m-2}=\M{v}_i \\ \vdots \quad & \vdots & \qquad \vdots \\ % & \qquad \vdots \\ m) \quad & \left( \M{A}-\lambda_i \M{I} \right) \M{u}_{i}^{m}=\M{u}_{i}^{m-1} & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{m} \M{u}_i^{m}=\M{0} % & \qquad \left( \M{A}-\lambda_i \M{I} \right)^{1} \M{u}_i^{2}=\M{v}_i \end{matrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>Pamiętaj jednak, że</strong> <ul> <li>Proszę jednak pamiętaj, że nie dla dowolnego wektora własnego istnieją wektory dołączone.</li> <li>Musimy nie jako wyznaczać te wektory uogólnione od najwyższego rzędu i potem schodzić niżej, tak jak miało to miejsce w naszych przykładach</li> </ul> <strong> *** Error message: Extra \endgroup. (in macro \document) leading text: \begin{document} Missing $ inserted. leading text: ...ex.com-9fb0e92389dca630ee0446940583ad35_ Bad math environment delimiter. leading text: ...ass="ql-img-displayed-equation " alt="\[ Improper \prevdepth. leading text: \end{document} Missing $ inserted. leading text: \end{document} Missing } inserted. leading text: \end{document} Missing } inserted. leading text: \end{document} Missing } inserted. leading text: \end{document} Missing \cr inserted. leading text: \end{document} Missing { inserted. leading text: \end{document} Missing { inserted. leading text: \end{document} Extra }, or forgotten $. leading text: \end{document} Extra }, or forgotten $. leading text: \end{document} Incompatible list can't be unboxed.\left( \M{A}-\lambda_i \M{I} \right)^{1}
 \left( \M{A}-\lambda_i \M{I} \right)^{2}
\left( \M{A}-\lambda_i \M{I} \right)^{2} \left( \M{A}-\lambda_i \M{I} \right)^{3}
\left( \M{A}-\lambda_i \M{I} \right)^{3} \ldots
\ldots \left( \M{A}-\lambda_i \M{I} \right)^{m}
\left( \M{A}-\lambda_i \M{I} \right)^{m} d_1
d_1 d_2
d_2 \ldots
\ldots d_{m}
d_{m} d_1 = n-\rank (\M{A}-\lambda_i\M{I})
d_1 = n-\rank (\M{A}-\lambda_i\M{I}) d_2 = n-\rank \left( (\M{A}-\lambda_i\M{I})^2\right)
d_2 = n-\rank \left( (\M{A}-\lambda_i\M{I})^2\right) \vdots
\vdots m
m \M{u}_i^{m}
\M{u}_i^{m} \left( \M{A}-\lambda_i \M{I} \right)^{m}
\left( \M{A}-\lambda_i \M{I} \right)^{m} \left( \M{A}-\lambda_i \M{I} \right)\cdot \M{u}_i^{m} = \M{u}_i^{m-1}
\left( \M{A}-\lambda_i \M{I} \right)\cdot \M{u}_i^{m} = \M{u}_i^{m-1} [n\times m]
[n\times m]![Rendered by QuickLaTeX.com </li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3e4d3cc227d06798e094f3dd2a2cfcfa_l3.png" height="35" width="202" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} v_i & \M{u}_i^{2} & \M{u}_i^{3} & \ldots & \M{u}_i^{m} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>Blok wektorów dla macierzy przejścia </strong> <ul> <li style="list-style-type: none;"> <ul> <li>Wyznaczyliśmy blok wektorów, dla macierz o wymiarach](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-02602040b0f83b655ece4f9a28a53bf9_l3.png)
[n\times m]
 m=s_ 1
m=s_ 1![Rendered by QuickLaTeX.com .</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6e2bf16e3ddbf6aaf509219488b8fe18_l3.png" height="35" width="318" class="ql-img-displayed-equation " alt="\[\M{W}_{i,1}=\begin{bmatrix} \M{v}_{i,1} & \M{u}_{i,1}^{2} & \M{u}_{i,1}^{3} & \ldots & \M{u}_{i,1}^{m} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li style="list-style-type: none;"> <ul> <li>Następnie w podobny sposób bloki wektorów dla kolejnej klatki stopnia](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0729b8b0970e8dac88086bb47dd31719_l3.png)
s_2,s_3, \ldots, s_{d_1}
![Rendered by QuickLaTeX.com .</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b9cc2bbb80ab1c17e77690b5bd336dd3_l3.png" height="35" width="318" class="ql-img-displayed-equation " alt="\[\M{W}_{i,2}=\begin{bmatrix} \M{v}_{i,2} & \M{u}_{i,2}^{2} & \M{u}_{i,2}^{3} & \ldots & \M{u}_{i,2}^{s_2} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li style="list-style-type: none;"> <ul> <li>itd.</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-877e2f0543326cf73ab3b6e2c25cd411_l3.png" height="35" width="360" class="ql-img-displayed-equation " alt="\[\M{W}_{i,d_1}=\begin{bmatrix} \M{v}_{i,d_1} & \M{u}_{i,d_1}^{2} & \M{u}_{i,d_1}^{3} & \ldots & \M{u}_{i,d_1}^{s_3} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>... Ale UWAGA</strong> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6e2bf16e3ddbf6aaf509219488b8fe18_l3.png" height="35" width="318" class="ql-img-displayed-equation " alt="\[\M{W}_{i,1}=\begin{bmatrix} \M{v}_{i,1} & \M{u}_{i,1}^{2} & \M{u}_{i,1}^{3} & \ldots & \M{u}_{i,1}^{m} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b9cc2bbb80ab1c17e77690b5bd336dd3_l3.png" height="35" width="318" class="ql-img-displayed-equation " alt="\[\M{W}_{i,2}=\begin{bmatrix} \M{v}_{i,2} & \M{u}_{i,2}^{2} & \M{u}_{i,2}^{3} & \ldots & \M{u}_{i,2}^{s_2} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-999e9d8111a771619b91bf4539515acf_l3.png" height="35" width="360" class="ql-img-displayed-equation " alt="\[\M{W}_{i,d_1}=\begin{bmatrix} \M{v}_{i,d_1} & \M{u}_{i,d_1}^{2} & \M{u}_{i,d_1}^{3} & \ldots & \M{u}_{i,d_1}^{s_{d_1}} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li style="list-style-type: none;"> <ul> <li>Załóżmy, że masz już](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3642eefb674c37bbc876172d50d43785_l3.png)
\M{W}_{i,1}
 \M{u}_{i,{\R{2}}}^{s_2}
\M{u}_{i,{\R{2}}}^{s_2} \M{u}_{i,{\R{1}}}^{s_2}
\M{u}_{i,{\R{1}}}^{s_2} \M{u}_{i,2}^{s_2-1}
\M{u}_{i,2}^{s_2-1} \M{u}_{i,2}^{s_2-2}
\M{u}_{i,2}^{s_2-2} \M{v}_{i,2}
\M{v}_{i,2} \M{W}_{i,2}
\M{W}_{i,2} \M{u}_{i,{\R{3}}}^{s_{\R{3}}}
\M{u}_{i,{\R{3}}}^{s_{\R{3}}} \M{u}_{i,{\R{2}}}^{s_{\R{3}}}
\M{u}_{i,{\R{2}}}^{s_{\R{3}}} \M{u}_{i,{\R{1}}}^{s_{\R{3}}}
\M{u}_{i,{\R{1}}}^{s_{\R{3}}} \lambda_i
\lambda_i![Rendered by QuickLaTeX.com </strong> <ul> <li style="list-style-type: none;"> <ul> <li>Po uzyskaniu wszystkich macierzy składamy ją w większą, tak jak było wspomniane wcześniej</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-01408415d68e9c7caa8939ca8301367c_l3.png" height="82" width="303" class="ql-img-displayed-equation " alt="\[\M{W}_i = \begin{bmatrix} & & & \\ \M{W}_{i,1} & \M{W}_{i,2} & \ldots & \M{W}_{i,d_1} \\ & & & \\ \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li>Jest to blok wszystkich wektorów dla wszystkich wektorów własnych dla](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d450aea430796357450a8d38e8cf926d_l3.png)
\lambda_i
 \lambda_{i+1}
\lambda_{i+1} i
i![Rendered by QuickLaTeX.com </strong> <ul> <li style="list-style-type: none;"> <ul> <li>Jak zrobimy dla wszystkich to składamy wszystko w całość</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-2ced6ac72c8906e577129c4440364e5a_l3.png" height="24" width="136" class="ql-img-displayed-equation " alt="\[\M{A} = \M{W} \M{J} \M{W}^{-1},\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6c7c061aa1d5aaad1f98046d65bb1517_l3.png" height="116" width="490" class="ql-img-displayed-equation " alt="\[\M{J}= \begin{bmatrix} \M{J}_1 & \M{0} & \M{0} & \M{0} \\ \M{0} & \M{J}_2 & \M{0} & \M{0} \\ \vdots & \vdots & \ddots & \vdots \\ \M{0} & \M{0} & \ldots & \M{J}_{\R{r}} \end{bmatrix} \quad \M{W}= \begin{bmatrix} \M{W}_1 & \M{W}_2 & \ldots & \M{W}_{\R{r}} \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-31d508e45bcc7170920a4f58c87b0b4d_l3.png" height="139" width="543" class="ql-img-displayed-equation " alt="\[\M{J} = \begin{bmatrix} \M{K}_1 & \M{0} & \cdots & \M{0} \\ \M{0} & \M{K}_2 & \cdots & \M{0} \\ \vdots & \vdots & \ddots & \vdots \\ \M{0} & \M{0} & \cdots & \M{K}_{\R{q}} \\ \end{bmatrix} \qquad \M{K}_{\R{i}} = \begin{bmatrix} \lambda_{\R{i}} & 1 & 0 & \cdots & 0 \\ 0 & \lambda_{\R{i}} & 1 & \cdots & 0 \\ 0 & 0 & \lambda_{\R{i}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \lambda_{\R{i}} \\ \end{bmatrix},\]" title="Rendered by QuickLaTeX.com"/> <strong>Twierdzenie</strong> Wektory własne odpowiadające różnym wartościom własnym tego samego przekształcenia są liniowo niezależne. <strong>Definicja Wektor dołączony</strong> <strong>Definicja </strong> <ul> <li style="list-style-type: none;"> <ul> <li>Wektor](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-fb01d88597ffe1395414525fc0cc9504_l3.png)
\M{u}^p
 p
p \M{A}
\M{A} \lambda
\lambda![Rendered by QuickLaTeX.com Jeśli</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e4dadf112d97f17df642018a524bdcbe_l3.png" height="26" width="431" class="ql-img-displayed-equation " alt="\[(\M{A} -\lambda \M{I} )^p \M{u}^{p}=0 \qquad \wedge \qquad (\M{A} -\lambda \M{I} )^{p-1} \M{u}^{p} \neq 0\]" title="Rendered by QuickLaTeX.com"/> <strong>Macierz diagonalizowalna - pełna odpowiedź</strong> <strong>Warunek K-W diagonalizowalności</strong> Jeżeli](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-5284acdf200310fc5a3e06985d20dd7e_l3.png)
\lambda_1, \ldots \lambda_r
 \lambda_i
\lambda_i![Rendered by QuickLaTeX.com jest równa jej krotności geometrycznej, czyli <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4f1f1a34525bfd5bcecb4298b092cb00_l3.png" height="22" width="204" class="ql-img-displayed-equation " alt="\[k_i = \dim \ker (\M{A}-\lambda_i\M{I}),\]" title="Rendered by QuickLaTeX.com"/> to wtedy i tylko wtedy macierz jest diagonalizowalna. <strong>Uwaga inne konwencje </strong> <ul> <li>Niektórzy klatki Jordana definiują jako macierz, która na przekątnej ma wartość własną, a jedynki pod przekątną, a nie jak do tej pory nad przekątną.</li> <li>Jest równoważny zapis, lecz rzadziej spotykany.</li> <li>Należy wówczas pamiętać, iż wektory dołączone układamy w odwrotnej kolejności, niż tak jak robiliśmy przez cały ten film w kolumnach, macierzy przejścia, dla danej klatki Jordana.</li> </ul> <strong>Łatwe potęgowanie</strong> <ul> <li style="list-style-type: none;"> <ul> <li>Obserwacja</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c81c06bf79bfed1c5eea8442e808919c_l3.png" height="39" width="525" class="ql-img-displayed-equation " alt="\[\M{A}^3=\left( \M{W}\M{J}\M{W}^{1} \right)^3 = \left( \M{W}\M{J}\M{W}^{1} \right)\cdot \left( \M{W}\M{J}\M{W}^{1} \right)\cdot \left( \M{W}\M{J}\M{W}^{1} \right) =\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e15a362427f7be1814689833dc4265df_l3.png" height="47" width="373" class="ql-img-displayed-equation " alt="\[=\M{W}\M{J} \underbrace{\M{W}^{1}\M{W}}_{\M{I}} \M{J}\underbrace{\M{W}^{1}\M{W}}_{\M{I}}\M{J}\M{W}^{1}=\M{W}\M{J}^3\M{W}^{-1}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li style="list-style-type: none;"> <ul> <li>Wniosek</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e3f51491d53dd34b3d7d83296df87c07_l3.png" height="36" width="285" class="ql-img-displayed-equation " alt="\[\M{A}^n=\left( \M{W}\M{J}\M{W}^{1} \right)^n = \M{W}\M{J}^n\M{W}^{-1}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li>Może jest jeszcze łatwy sposób na obliczanie potęg macierzy](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-fe267d5182bbe01e9246e0f6db65dfbb_l3.png)
\M{J}
![Rendered by QuickLaTeX.com ?</li> </ul> <strong>Twierdzenie potęgowanie macierzy Jordana</strong> <ul> <li style="list-style-type: none;"> <ul> <li>Okazuje się, że zachodzi:</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4a13b33d1431bbbd856aee7f44ef4dc6_l3.png" height="117" width="508" class="ql-img-displayed-equation " alt="\[\M{J}^{\R{n}} =\left( \begin{bmatrix} \M{K}_1 & \M{0} & \cdots & \M{0} \\ \M{0} & \M{K}_2 & \cdots & \M{0} \\ \vdots & \vdots & \ddots & \vdots \\ \M{0} & \M{0} & \cdots & \M{K}_q \\ \end{bmatrix} \right)^{\R{n}} = \begin{bmatrix} \M{K}_1^{\R{n}} & \M{0} & \cdots & \M{0} \\ \M{0} & \M{K}_2^{\R{n}} & \cdots & \M{0} \\ \vdots & \vdots & \ddots & \vdots \\ \M{0} & \M{0} & \cdots & \M{K}_q^{\R{n}} \\ \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li>Zastanówmy się zatem czym jest potęga klatki Jordana</li> </ul> <strong>Potęgowanie klatek Jordana</strong> <ul> <li style="list-style-type: none;"> <ul> <li>Potęgując klatki Jordana stopnia 2, szybko zaobserwujemy powtarzający się wzorzec</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c80ac79210fb6726eba4f36866e0ae58_l3.png" height="62" width="174" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 \\ 0 & a \end{bmatrix}^2 = \begin{bmatrix} a^2 & 2a \\ 0 & a^2 \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f683524f5697d3cfb6f5715d293f33f4_l3.png" height="62" width="174" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 \\ 0 & a \end{bmatrix}^3 = \begin{bmatrix} a^3 & 3a \\ 0 & a^3 \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-27fd7e4403abbb46c483a1cf938a3fb0_l3.png" height="62" width="174" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 \\ 0 & a \end{bmatrix}^4 = \begin{bmatrix} a^4 & 4a \\ 0 & a^4 \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c9a867fadad3fd61f20c5a6f271a6f51_l3.png" height="59" width="180" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 \\ 0 & a \end{bmatrix}^n = \begin{bmatrix} a^n & na \\ 0 & a^n \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>Potęgowanie klatek Jordana</strong> <ul> <li style="list-style-type: none;"> <ul> <li>Klatka stopnia 3</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-82aaf5c78b3e9b94bb95ca959f03f795_l3.png" height="85" width="250" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 & 0 \\ 0 & a & 1 \\ 0 & 0 & a \end{bmatrix}^2 = \begin{bmatrix} a^2 & 2a & 1 \\ 0 & a^2 & 2a \\ 0 & 0 & a^2 \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6545b1151a4d6e7c3e2d28254bb73c59_l3.png" height="85" width="250" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 & 0 \\ 0 & a & 1 \\ 0 & 0 & a \end{bmatrix}^3 = \begin{bmatrix} a^3 & 3a & 3a \\ 0 & a^3 & 3a \\ 0 & 0 & a^3 \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3865d7b898631138a7a8b740ab5acf68_l3.png" height="83" width="361" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 & 0 \\ 0 & a & 1 \\ 0 & 0 & a \end{bmatrix}^n = \begin{bmatrix} a^n & na^{n-1} & \frac{n(n-1)a^{n-2}}{2} \\ 0 & a^n & na^{n-1} \\ 0 & 0 & a^n \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>Potęgowanie klatek Jordana</strong> <ul> <li style="list-style-type: none;"> <ul> <li>Klatka stopnia](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-40e0ac34b7134f07e54addd27dda96c6_l3.png)
k
![Rendered by QuickLaTeX.com </li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-296c1fc9e5cfebfd0be6fd0f9d66942e_l3.png" height="165" width="511" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 & 0 & \ldots & 0 \\ 0 & a & 1 & \ldots & 0 \\ 0 & 0 & a & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & a \\ \end{bmatrix}^n = \begin{bmatrix} a^n & (a^n)' & \frac{(a^n)''}{2!} & \ldots & \frac{(a^n)^{(k)}}{k!} \\ 0 & a^n & (a^n)' & \ldots & \frac{(a^n)^{(k-1)}}{(k-1)!} \\ 0 & 0 & a^n & \ldots & \frac{(a^n)^{(k-2)}}{(k-2)!} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & a^n \\ \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <ul> <li style="list-style-type: none;"> <ul> <li>Mamy przepis na łatwe potęgowanie do dowolnej potęgi dowolnej macierzy, o ile dysponujemy rozkładem Jordana, tej macierzy</li> </ul> </li> </ul> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-555ca6cbaf18e45a35774d3651936345_l3.png" height="115" width="330" class="ql-img-displayed-equation " alt="\[A^{\R{n}}=\M{W} \begin{bmatrix} \M{K}_1^{\R{n}} & \M{0} & \cdots & \M{0} \\ \M{0} & \M{K}_2^{\R{n}} & \cdots & \M{0} \\ \vdots & \vdots & \ddots & \vdots \\ \M{0} & \M{0} & \cdots & \M{K}_q^{\R{n}} \\ \end{bmatrix} \M{W}^{-1}\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-296c1fc9e5cfebfd0be6fd0f9d66942e_l3.png" height="165" width="511" class="ql-img-displayed-equation " alt="\[\begin{bmatrix} a & 1 & 0 & \ldots & 0 \\ 0 & a & 1 & \ldots & 0 \\ 0 & 0 & a & \ldots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & a \\ \end{bmatrix}^n = \begin{bmatrix} a^n & (a^n)' & \frac{(a^n)''}{2!} & \ldots & \frac{(a^n)^{(k)}}{k!} \\ 0 & a^n & (a^n)' & \ldots & \frac{(a^n)^{(k-1)}}{(k-1)!} \\ 0 & 0 & a^n & \ldots & \frac{(a^n)^{(k-2)}}{(k-2)!} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & a^n \\ \end{bmatrix}\]" title="Rendered by QuickLaTeX.com"/> <strong>Kolejne kroki dalej</strong> <ul> <li style="list-style-type: none;"> <ul> <li>Skoro możemy łatwo potęgować, to w zasadzie możemy obliczyć dowolny wielomian od dowolnej macierzy</li> <li>W takim razie jesteśmy w stanie zdefiniować także dowolną funkcję od macierzy, o ile ta funkcja jest rozwijalna we szereg Taylora.</li> <li>W rozwinięciu Taylora jest tylko potęgowanie macierzy, ich skalowanie przez liczb i ich dodawanie.</li> <li>Co więcej okazuje się że dla dowolnej funkcji](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-922c0840155d4d6336dd4b6b5bba72ac_l3.png)
f$ rozwijalnej w szereg Taylora mamy:
-
![]()
Źródła
-
- В. В. Колыбасова, Н. Ч. Крутицкая, А. В. Овчинников – ЖОРДАНОВА ФОРМА МАТРИЦЫ ОПЕРАТОРА
math.phys.msu.ru/data/25/JF.pdf
-
- Michał Góra – Algebra liniowa – wykłady – Automatyka i robotyka
home.agh.edu.pl/~gora/algebra_ggios/Wyklad08.pdf
home.agh.edu.pl/~gora/algebra/Wyklad09.pdf
-
- Anna Zamojska-Dzienio – Algebra liniowa – konspekt wykładu
- Mariusz Przybycień – Matematyczne Metody Fizyki I – wykład 15
http://home.agh.edu.pl/~mariuszp/wfiis_mmf/index.html
-
- Ireneusz Nabiałek – zadania z algebry liniowej
- Rakesh Jana – Jordan Canonical Form – Notes on Linear Algebra
- How to Find Bases for Jordan Canonical Forms
www.math.ucla.edu/~jlindquist/115B/JCFBases.pdf
-
- K. R. MATTHEWS – LINEAR ALGEBRA NOTES – The Real Jordan Form
http://www.numbertheory.org/courses/MP274/
-
- Xingzhi Zhan – Extremal sparsity property
of the Jordan canonical form


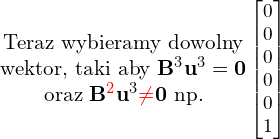








Bardzo ciekawy artykuł. Niesamowite, że potrafi się Pan aż tak zaangażować. Więcej piszę o tym na YouTube.
Ten fragment był śmieszny:
“Przy czym wcale \textbf{nie} jest powiedziane” 😀