Interpretacja wzoru Eulera (Euler’s formula)

Posted on by Mateusz Kowalski

Wzór Eulera wygląda następująco.

    \[ \boxed{e^{it}=\cos t + i \sin t} \]

Mamy tu porównanie liczby zespolonej w postaci wykładniczej

    $$z= |z| \cdot e^{i \arg z}$$

o module równym 1. Z reprezentacją algebraiczną

    $$z = a+bi $$

Mamy zatem

    $$ |z| \cdot e^{i \arg z}=a + bi$$

moduł liczby zespolonej to

    $$ |z| =\sqrt{a^2 + b^2}$$

Jeżeli przyjmiemy, że weźmiemy liczbę o module 1, czyli

    $$ a^2 + b^2=1$$

to uzyskamy:

    $$ e^{i \arg z} =a + bi$$

Wzór Eulera mówi, że w tym przypadku a i b musi być równe.

    $$ a= \cos(\arg z) $$

    $$ b=\sin(\arg z)$$

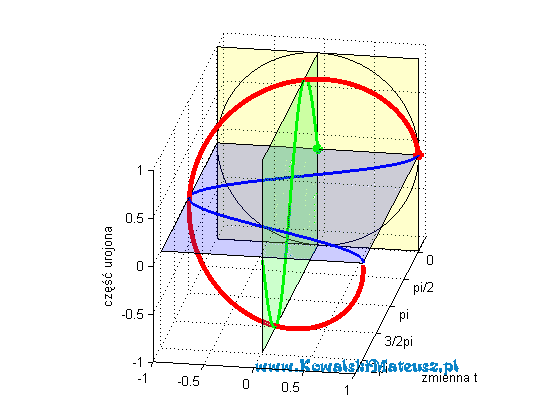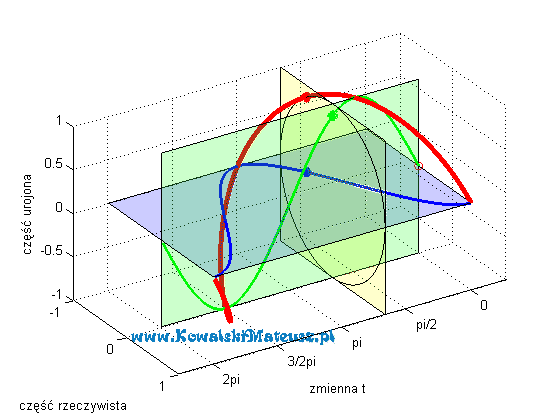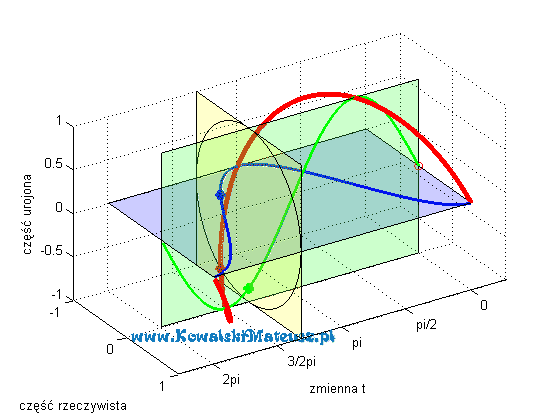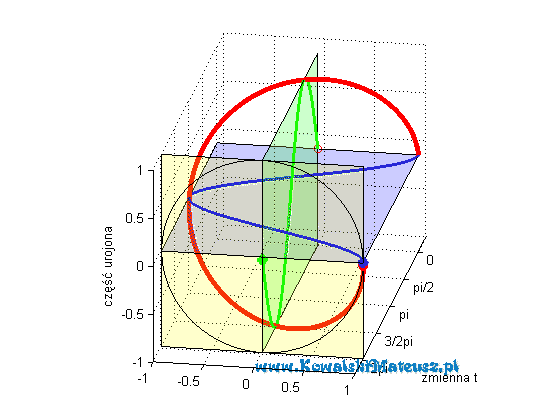
Poniżej prezentuje animacje w jasny sposób obrazująca cała tą tożsamość.
Wzór Eulera

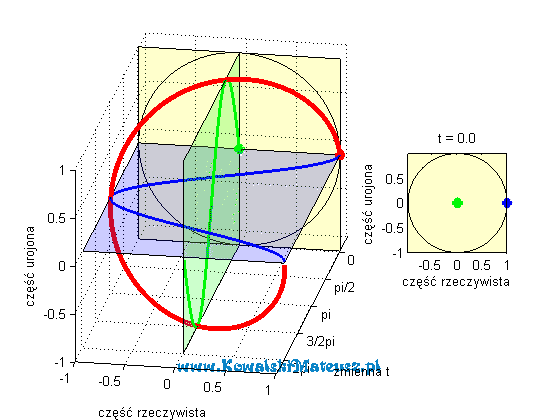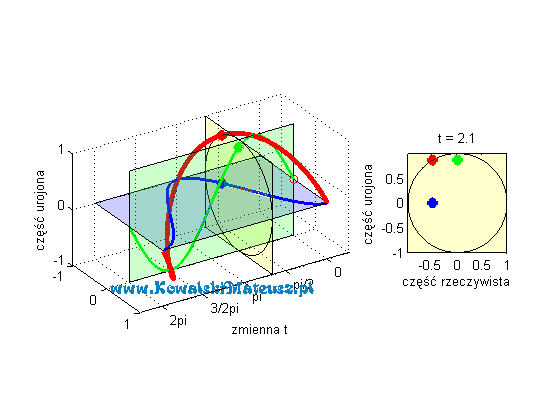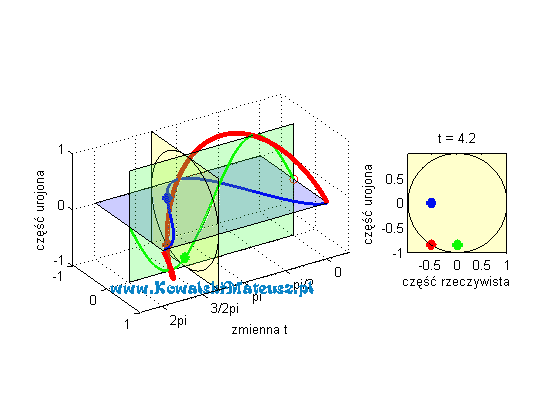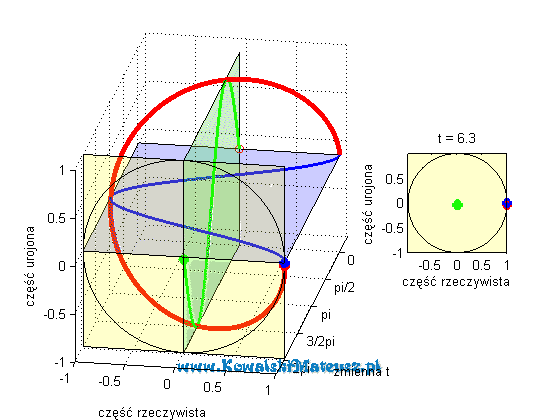
Kosinusoida niebieska to cześć rzeczywista liczby zespolonej o module 1. A sinusoida zielona jest to cześć urojona tej samej liczby zespolonej. która leży w płaszczyźnie prostopadłej do płaszczyzny w której leży część rzeczywista (niebieska kosinusoida).
Czerwona linia to suma tych dwóch wartości (rzeczywistej i urojonej), czyli wartość zespolona. Ma ona kształt “sprężynki”.

A tu powiększona wersja
tożsamość Eulera

Be Sociable, Share!

Comments

comments

6 thoughts on “Interpretacja wzoru Eulera (Euler’s formula)”

  1. Dziękuję Mateuszu.

    Pozwoliłem sobie, promować Ciebie na swoim profilu.

    Życzę Ci
    dalszych tak świetnych i kolorowych
    wyjaśnień matematycznych ze
    wszelkimi ciekawymi nowościami i urozmaiceniami.

    🙂

    Jarek Jaworski

    Odpowiedz
  3. Kasia

    Jestem w nagłej potrzebie nabycia wiedzy matematycznej i przypomniałam sobie o Twoich kursach.
    Bardzo mi pomagają w zrozumieniu tej zawiłej i trudnej dla mnie dziedziny nauki;)
    Dziękuje Mateuszu, jesteś WIELKI!!!!

    Odpowiedz

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.