Ostatnio zaciekawiłem się formatem png a dokładniej pewną możliwością jakie ten format daje. Chodzi o to, że można w tym formacie zrobić animacje coś jak animacja w formacie gif. Animowany png jest kompatybilny ze zwykłym png. Jednak nie wszystkie przeglądarki i programy obsługują ten format. Czym się różni od gif tym, że nie ma ograniczenia na 256 kolorów jak to ma miejsce w gifie. Umiejętne zapisanie pozwala ponadto zaoszczędzić około 20 % objętości pliku w porównaniu do gif, przy tej samej palecie barw . Ponadto jak już wspomniałem jest kompatybilny ze zwykłym png, co oznacza, że starsze przeglądarki animowanego png będą wiedziały jako jedno zdjęcie (pierwsze). Same plusy jedyny minus to, że nie wszystko go obsługuję.
Ja osobiście szukałem sposobu jak tworzyć takie animowane png no i mi się udało
efekt poniżej.
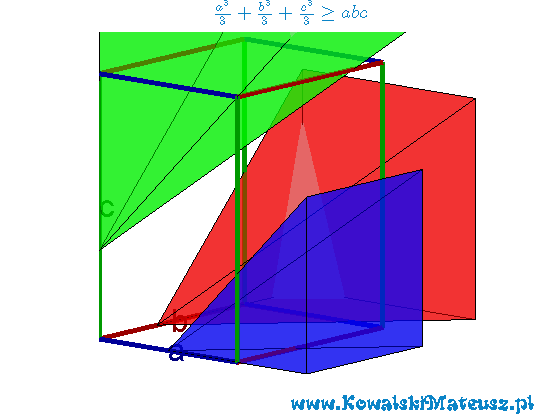
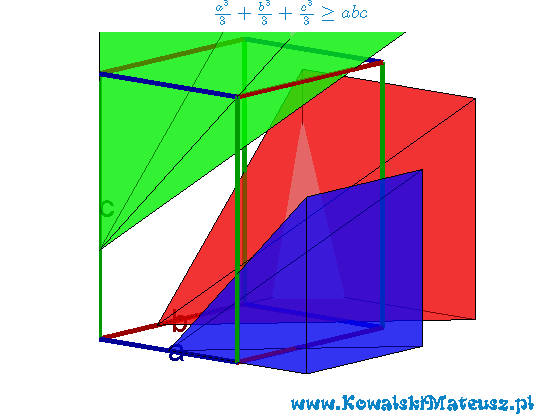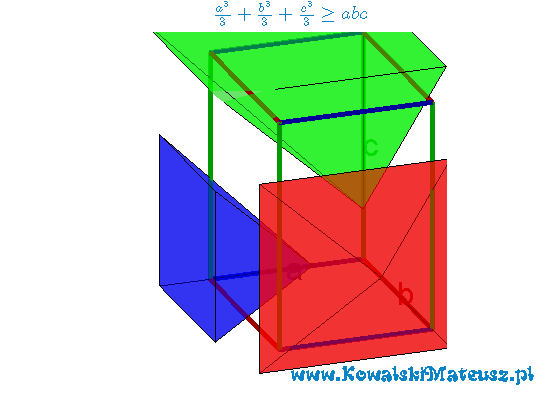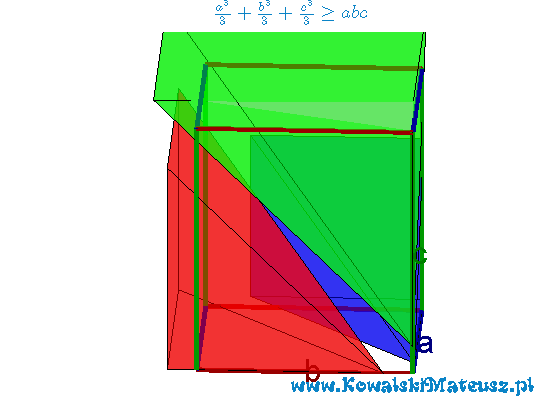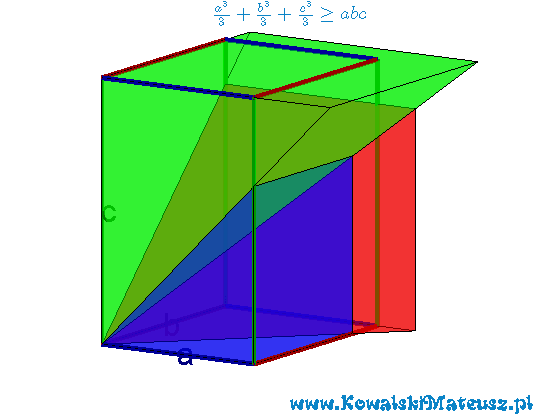
Powyżej animacja png poniżej animacja gif.
Teraz przejdźmy do matematyki.
Aby przy okazji zrobić coś pożytecznego postanowiłem udowodnić geometrycznie pewną nierówność, która jest słuszna dla ![]() .
.
Pokażemy, że ![]() . Znasz zapewne wzór na objętość ostrosłupa.
. Znasz zapewne wzór na objętość ostrosłupa.
![]() .
.
Objętość nie zależy od kształtu podstawy, ani kształtu całej bryły znaczenie ma pole podstawy i długość wysokości. Co prezentuje poniższa animacja.

Jeśli za podstawę przyjmiemy kwadrat o boku ![]() , a za wysokość także
, a za wysokość także ![]() wówczas objętość takiego ostrosłupa wynosić będzie
wówczas objętość takiego ostrosłupa wynosić będzie ![]() . Skoro powiedzieliśmy sobie, że kształt możemy wziąć dowolny to weźmy taki, którego rzut wysokości na podstawę znajduje się w narożniku kwadratowej podstawy.
. Skoro powiedzieliśmy sobie, że kształt możemy wziąć dowolny to weźmy taki, którego rzut wysokości na podstawę znajduje się w narożniku kwadratowej podstawy.
Biorąc jeszcze 2 ostrosłupy, podobne do tego ostrosłupa tylko o krawędzi równej odpowiednio ![]() oraz
oraz ![]() możemy je potem ułożyć tak jak jest to przedstawione na pierwszej animacji. Widać wyraźnie, że ich objętość jest większa od objętości prostopadłościanu o krawędziach
możemy je potem ułożyć tak jak jest to przedstawione na pierwszej animacji. Widać wyraźnie, że ich objętość jest większa od objętości prostopadłościanu o krawędziach ![]() . W skrajnym wypadku może być równa jeśli zachodzić będzie
. W skrajnym wypadku może być równa jeśli zachodzić będzie ![]() wtedy 3 jednakowe ostrosłupy utworzą sześcian.
wtedy 3 jednakowe ostrosłupy utworzą sześcian.
Zauważ ponadto, że ![]()








