Twierdzenie Euler'a o Iloczynie Sum 4 Kwadratów Liczb

Streszczenie
1. Powiemy sobie o twierdzeniu Eulera o iloczynie sum kwadratów
2. Podamy także dowód tego twierdzenia
3. Dlaczego nie udowodnimy tego twierdzenia w klasyczny sposób
4. Dowód z wykorzystaniem kwaternionów znaczniej prostszy i krótszy
5. I co z tego wszystkiego

Zacznijmy sobie od pewnego twierdzenia iloczynie sum 4 kwadratów liczb rzeczywistych.

$\begin{twie} [] $ $ \\ Dla każdych $s_1,s_2,x_1,x_2,y_1,y_2,z_1,z_2 \in \RR$ istnieją takie liczby $s_3,x_3,y_3,z_3\in \RR$, że zachodzi: $$(s_1^2+x_1^2+y_1^2+z_1^2)\cdot(s_2^2+x_2^2+y_2^2+z_2^2)=(s_3^2+x_3^2+y_3^2+z_3^2),$$ \end{twie}$

Twierdzenie w tej formie nie jest warte uwagi, gdyż biorąc kwadraty dowolnych 8 liczby rzeczywistych, mnożąc je ze sobą i dodając na wszelki możliwy sposób uzyskamy liczbę rzeczywistą dodatnią $d$ . Zatem zawsze istnieje jej pierwiastek $w$ , taki że $w^2=d$ . Skoro tak, to tym bardziej istnieją 4 liczby, takie że $w_1^2+w_2^2+w_3^2+w_4^2=d$ , bo w szczególności wystarczy przyjąć $w_2=w_3=w_4=0$ .

Jednak twierdzenie, co jest już bardziej ciekawe, jest prawdziwe dla liczb całkowitych.

$\begin{twie} [Eulera o iloczynie sum kwadratów] $ $ \\ \label{t:eulera} Dla każdych $s_1,s_2,x_1,x_2,y_1,y_2,z_1,z_2 \in \R{\ZZ}$ istnieją takie liczby $s_3,x_3,y_3,z_3\in \R{\ZZ}$, że zachodzi: $$(s_1^2+x_1^2+y_1^2+z_1^2)\cdot(s_2^2+x_2^2+y_2^2+z_2^2)=(s_3^2+x_3^2+y_3^2+z_3^2),$$ \end{twie}$

Chcąc to dowieść w sposób klasyczny
wyszlibyśmy sobie od lewej strony i pomnożyli dwa nawiasy. W efekcie powstało by 16 wyrazów jednak ten tasiemiec nie jest wcale najgorsze. Wymieńmy wady tego co trzeba zrobić dalej w tej metodzie:

  1. Trzeba dopisać pewne wyrazy na zasadzie $+a-a$ ,
     tak by wartość się nie zmieniła, a postać wyrażenia.
  2. Ponadto trzeba się skapnąć co trzeba dopisać.
  3. Trzeba to zrobić kilka razy w efekcie powstanie tasiemiec
     zawierający przynajmniej 24 wyrazy.
  4. Trzeba znać wzór skróconego mnożenia na kwadrat sumy 4 składników
     $(a+b+c+d)^2=a^2+b^2+c^2+d^2+2ab+2ac+2ad+2bc+2bd+2cd$
  5. Zastosować go nie w kierunku rozwijania tylko zwijania
  6. Co więcej trzeba ten wzór użyć 4 krotnie
Nie wspominam już, że z tego tasiemca trzeba wybrać odpowiednie wyrazy do danego wzoru, aby się zwinął.

Dowód z użyciem kwaternionów
Dowód znacznie się upraszcza w przypadku użycia kwaternionów. Nie mówię że tego nie można udowodnić klasycznie, ale jest to strasznie czasowe. Bardzo prawdopodobne, że Euler właśnie tak to zrobił, gdyż za jego czasów nie było jeszcze kwaternionów.

Podstawowe potrzebne informacje na temat kwaternionów
kwaternion jest liczbą którą można zapisać np. tak
$q=s+x\M{i}+y\M{j}+z\M{k}$ , gdzie $\M{i},\M{j},\M{k}$ to pewne stałe, a dokładnie są to jednostki urojone definiowane jako 4 równości
$\M{i}^2=\M{j}^2=\M{k}^2=\M{ijk}=-1$
Warto wiedzieć także, że mnożenie kwaternionów nie jest przemienne, tzn $q_1\cdot \q_2 \neq \q_2\cdot\q_1$ Z 4 równości a dotyczących jednostek urojonych możemy wywnioskować, iż
$\boxed{\M{i}\cdot\M{j}=k} \qquad \boxed{\M{j}\cdot\M{k}=i} \qquad \boxed{\M{k}\cdot\M{i}=j}$
$\boxed{\M{j}\cdot\M{i}=-k} \qquad \boxed{\M{k}\cdot\M{j}=-i} \qquad \boxed{\M{i}\cdot\M{k}=-j}$
Zdefiniujmy sobie jeszcze takie liczby, które możemy przypisać danemu kwaternionowi.
$|q|=\sqrt{s^2+x^2+y^2+z^2+z^2}$ nazywamy modułem kwaternionów natomiast
$|q|^2=s^2+x^2+y^2+z^2+z^2$ nazywamy normą kwaternionu, lecz uwaga niektórzy autorzy za normę kwaternionu uważają moduł kwaternionu także uważaj jak będziesz szukał informacji na ten temat. W istocie moduł kwaternionu także spełnia warunki normy.
Potrzebna będzie nam jeszcze tożsamość, która mówi
$|q_1q_2|=|q_1|\cdot|q_2|$

Dowód Twierdzenie Euler’a
Niech dane będą dwa kwaterniony $\xi_1 , \xi_2 \in \HH(\ZZ)$
$\xi_1 =s_1 - x_1\M{i} - y_1\M{j} - z_1\M{k},$
$\xi_2 =s_2 + x_2\M{i} + y_2\M{j} + z_2\M{k}.$
Iloczyn norm tych kwaternionów jest równy:
$|\xi_1|^2|\xi_2|^2 = (s_1^2 + x_1^2 + y_1^2 + z_1^2)(s_2^2 + x_2^2 + y_2^2 + z_2^2).$
Iloczyn kwaternionów zaś:

$\begin{alignat*}{5} &\xi_1 \xi_2 &=& (s_1 - x_1\M{i} - y_1\M{j} - z_1\M{k})(s_2 + x_2\M{i} + y_2\M{j} + z_2\M{k})=\R{...}\\ &&=& (s_1s_2 + x_1x_2 + y_1y_2 + z_1z_2) + (s_1x_2 - x_1s_2 - y_1z_2 + z_1y_2)\M{i} + \\ &&+& (s_1y_2 + x_1z_2 - y_1s_2 - z_1x_2)\M{j} + (s_1z_2 - x_1y_2 + y_1x_2 - z_1s_2)\M{k}. \end{alignat*}$

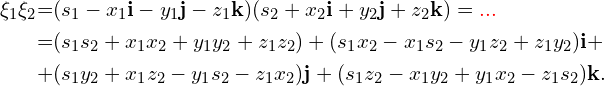
Norma z tego iloczynu wynosi:

$\begin{alignat*}{5} &|\xi_1 \xi_2|^2 &=& (\underbrace{ s_1s_2 + x_1x_2 + y_1y_2 + z_1z_2}_{\in \ZZ})^2 + (\underbrace{ s_1x_2 - x_1s_2 - y_1z_2 + z_1y_2}_{\in \ZZ})^2 + \\ &&+& (\underbrace{ s_1y_2 + x_1z_2 - y_1s_2 - z_1x_2}_{\in \ZZ})^2 + (\underbrace{s_1z_2 - x_1y_2 + y_1x_2 - z_1s_2}_{\in \ZZ})^2, \end{alignat*}$

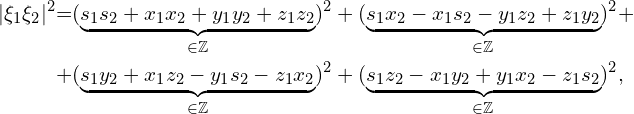
a przecież na mocy twierdzenia o iloczynie norm dwóch kwaternionów mamy
$|\xi_1|^2\cdot |\xi_2|^2=|\xi_1 \xi_2|^2$ , czyli
$(s_1^2+x_1^2+y_1^2+z_1^2)\cdot(s_2^2+x_2^2+y_2^2+z_2^2)=(s_3^2+x_3^2+y_3^2+z_3^2).$
co należało dowieść.