Wielomianowa Krzywa Béziera 3 Stopnia Jako Funkcja f(x) [Wideo]

Jak znaleźć funkcję $f(x)$ daną parametrycznie, czyli w sposób typowy dla krzywych?

Wielomianowa krzywa Béziera o punktach kontrolnych

$\left( \quad (-1,-1), \quad (0,-1), \quad (0,1), \quad (1,1) \quad \right)$

Ma wzór parametryczny

$\begin{alignat*}{9} x(t) &=& 2t^3 -3t^2 +3t -1 \\ y(t) &=& -4t^3 +6t^2 -1 \end{alignat*},$

gdzie $t\in [0,1]$

Szukamy wzoru $t= ?$

$x(t) = 2t^3 -3t^2 +3t -1$

Aby wyznaczyć $t$ w zależności od $x$ należy rozwiązać równanie 3 stopnia z parametrem $x$

$2t^3-3t^2+3t-1-x=0$

$p = \frac{-b^2}{3a^2}+\frac{c}{a}=\frac{-9}{12} + \frac{3}{2} = \frac{3}{4}$

$q = \frac{2b^3}{27a^3} - \frac{bc}{3a^2} + \frac{d}{a} = \frac{-27\cdot 2}{27\cdot 8} -\frac{-9}{12}+\frac{-x-1}{2} = \frac{-x}{2}$

$\Delta = q^2+4\frac{p^3}{3^3} = \frac{x^2}{4} +\frac{1}{16}>0$

Wzór na $t(x)$
Rozwiązaniem równanie $w^3+pw+q=0$

$w = \sqrt[3]{\frac{-q}{2}+\frac{\sqrt{\Delta}}{2}} + \sqrt[3]{\frac{-q}{2}-\frac{\sqrt{\Delta}}{2}}=$

$=\underbrace{\sqrt[3]{\frac{x}{4}+\frac{\sqrt{4x^2+1}}{8}} }_{\alpha}+ \underbrace{\sqrt[3]{\frac{x}{4}-\frac{\sqrt{4x^2+1}}{8}}}_{\beta}$

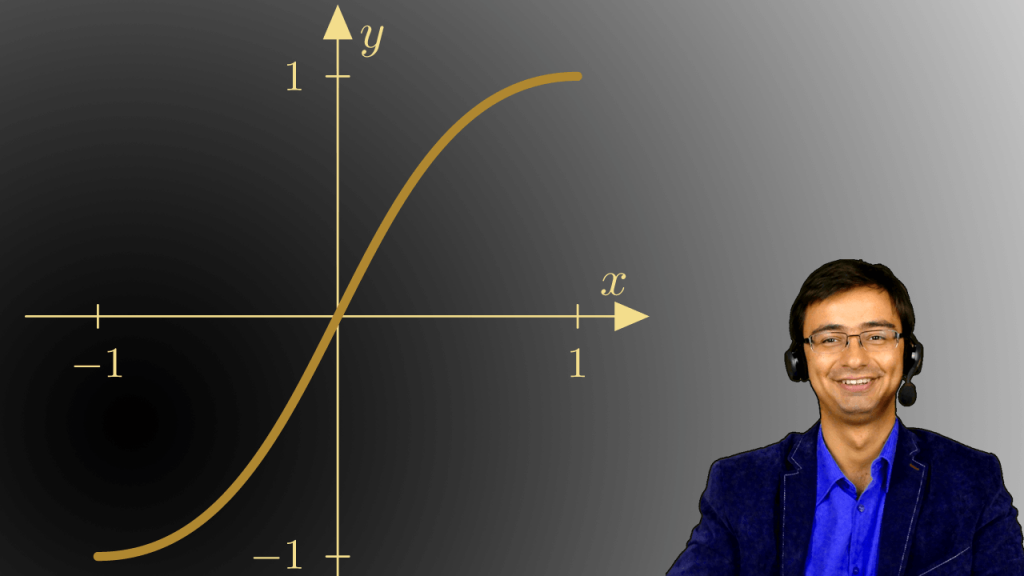
Mamy już teraz na funkcję $t(x)$

$t = w - \frac{b}{3a} = \frac{1}{2} + \alpha + \beta$

Skąd wiem, że $t$ jest funkcją $x$ ?

bo funkcja $x(t)$ jest rosnąca, to zaś wiadomo, ponieważ $x'(t) > 0$
W istocie $x'(t) = 6t^2-6t+3$ , ta funkcja kwadratowa nie ma miejsc zerowych, a skoro współczynnik przy $t^2$ jest dodatni, to $x'(t)>0$ co należało pokazać.
Istnieje zatem funkcja odwrotna $t(x)$

Jak wstawić do $y(t)$ funkcję $t(x)$ ?
Jako że teraz będziemy wstawiać za $t$ do wzoru funkcji $y$ , a tam pojawia się $t^2$ i $t^3$ , to obliczmy je na boku.
Potrzebne nam będą wzory skróconego mnożenia

$(a+b+c)^2 = a^2+b^2+c^2 + 2(ab+ac+bc)$

$(a+b+c)^3 = a^3+b^3+c^3 + 3(a^2b+ab^2+a^2c+ac^2+b^2c+bc^2)+6abc$

Zastosujmy i obliczmy

$t = \frac{1}{2} + \underbrace{\sqrt[3]{\frac{x}{4}+\frac{\sqrt{4x^2+1}}{8}} }_{\alpha}+ \underbrace{\sqrt[3]{\frac{x}{4}-\frac{\sqrt{4x^2+1}}{8}}}_{\beta}$

$(a+b+c)^2 = a^2+b^2+c^2 + 2(ab+ac+bc)$

$(a+b+c)^3 = a^3+b^3+c^3 + 3(a^2b+ab^2+a^2c+ac^2+b^2c+bc^2)+6abc$

$t^2 = \frac{1}{4}+ \alpha^2 +\beta^2 +\alpha +\beta +2\alpha\beta$

$t^3 = \frac{1}{8} +\alpha^3 + \beta^3 +3(\frac{\alpha}{4} + \frac{\alpha^2}{2} + \frac{\beta}{4} +\frac{\beta^2}{2} +\alpha^2\beta +\alpha\beta^2 ) + 3\alpha\beta$

$t = \frac{1}{2} + \underbrace{\sqrt[3]{\frac{x}{4}+\frac{\sqrt{4x^2+1}}{8}} }_{\alpha}+ \underbrace{\sqrt[3]{\frac{x}{4}-\frac{\sqrt{4x^2+1}}{8}}}_{\beta}$

$t^2 = \frac{1}{4}+ \alpha^2 +\beta^2 +\alpha +\beta +2\alpha\beta$

$t^3 = \frac{1}{8} +\alpha^3 + \beta^3 +3(\frac{\alpha}{4} + \frac{\alpha^2}{2} + \frac{\beta}{4} +\frac{\beta}{2} +\alpha^2\beta +\alpha\beta^2 ) + 3\alpha\beta$

$y(t) = -4t^3+6t^2-1$

$y = -\frac{1}{2} -4\alpha^3 - 4\beta^3 + 3(-\alpha -2\alpha^2 - \beta -2\beta^2 - 4\alpha^2\beta - 4\alpha\beta^2 ) +$

$-12\alpha\beta + \frac{3}{2} + 6\alpha^2 + 6\beta^2 + 6\alpha +6 \beta +12 \alpha\beta -1$

Wzór funkcji $f(x)$ jest blisko

$y = -\frac{1}{2} -4\alpha^3 - 4\beta^3 + 3(-\alpha -2\alpha^2 - \beta -2\beta^2 - 4\alpha^2\beta - 4\alpha\beta^2 ) +$

$-12\alpha\beta + \frac{3}{2} + 6\alpha^2 + 6\beta^2 + 6\alpha +6 \beta +12 \alpha\beta -1$

$y = 3\alpha + 3\beta -4(\alpha^3 +\beta^3 ) -12\alpha\beta(\alpha + \beta )$

$y = (\alpha + \beta ) (3 - 12 \alpha\beta ) -4 (\alpha^3+ \beta^3)$

$\alpha\beta=?$ oraz $\alpha^3 + \beta^3=?$

$\alpha = \sqrt[3]{\frac{x}{4}+\frac{\sqrt{4x^2+1}}{8}}$

$\beta = \sqrt[3]{\frac{x}{4}-\frac{\sqrt{4x^2+1}}{8}}$

$\alpha\beta = \sqrt[3]{\left( \frac{x}{4} + \frac{\sqrt{4x^2+1}}{8} \right)\left( \frac{x}{4} - \frac{\sqrt{4x^2+1}}{8} \right)} =\sqrt[3]{\frac{x^2}{16} - \frac{4x^2+1}{64}} = \frac{-1}{4}$

$\alpha^3+\beta^3 = \frac{x}{4} + \frac{\sqrt{4x^2+1}}{8} + \frac{x}{4} - \frac{\sqrt{4x^2+1}}{8} =\frac{x}{2}$

Wzór funkcji $f(x)$

$\alpha\beta = \frac{-1}{4}$

$\alpha^3+\beta^3 = \frac{x}{2}$

$y = (\alpha + \beta ) (3 - 12 \alpha\beta ) -4 (\alpha^3+ \beta^3)$

$y = -2x + 6(\alpha+\beta)$

$y = -2x + 6\left[ \ \sqrt[3]{\frac{x}{4} + \frac{\sqrt{4x^2+1}}{8}} + \sqrt[3]{\frac{x}{4} - \frac{\sqrt{4x^2+1}}{8}} \ \right]$

Co nam to dało?
Oba opisy krzywej są nieunormowane, lecz
Możliwość aproksymacji wzorem Taylora
Możliwość łatwego równomiernego próbkowania – co ma walory praktyczne

Ogólniej
Jakby ktoś chciał spróbować to może podjąć wyzwanie wyznaczenia wzoru $f(x)$ krzywej Beziera 3 stopnia zdeterminowanej przez punkty kontrolne ogólnie

$\begin{bmatrix} A & B & C & D \\ E & F & G & H \end{bmatrix}$