Nagranie 2
Praca domowa:
Zad 1.
Sprawdź czy funkcja ma pochodną w punkcie ![]() .
.
a) 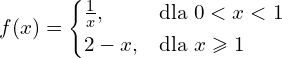
b) 
Zad 2.
Sprawdź czy funkcja ma pochodną w punkcie ![]() .
.
a) ![]()
b) ![]()
c) ![]()
d) 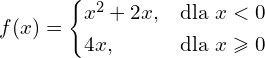
Zad 3.
Dobierz takie wartości ![]() i
i ![]() , aby funkcja
, aby funkcja  miała pochodną dla argumentu
miała pochodną dla argumentu ![]()
Zad 4.
Oblicz pochodną funkcji
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
g) ![]()
h) ![]()
Rozwiązania Kliknij aby zobaczyć rozwiązania









Dziękuję. Świetna była ta lekcja. Pomogła mi zrozumieć, dlaczego te wzory na pochodne są takie, a nie inne. Nie wiedziałem, że pochodna (nawę niewłaściwa) nie zawsze istnieje.
![Rendered by QuickLaTeX.com \left[ \sqrt[n]{x} \right]^\prime = \frac{x^{\frac{1}{n}-1} }{n}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b17eaa59e32e5cef294f23dfe47aaca9_l3.png)
Chyba zapomniał Pan o wzorze:
Przepraszam za ten informatyczny zapis, ale mam nadzieję, że Pan go odczyta.
Jeszcze raz przepraszam. Chodziło mi o pochodną z tego pierwiastka, a nie pierwiastek. Zapomniałem dopisać ‘ z lewej strony równania.
Poprawiłem twój wzór, aby był bardziej czytelny możesz używać latex’a do pisania wzorów jak znasz wstawiając wzór w znaczniki![Rendered by QuickLaTeX.com \left[x^n\right]^\prime = nx^{n-1}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-745126a1f87fe585885ccce4ca7fb289_l3.png) , bo działa również dla n rzeczywistego.
, bo działa również dla n rzeczywistego.
[] []wpisując w pierwszy nawias kwadratowytex, a w drugi/tex, a pomiędzy nie wór latex. W zasadzie to masz rację lecz ten wzór zawiera się wTym razem praca domowa okazała się łatwiejsza. Nie umiem odpowiedzieć tylko na zadanie nr 3. Reszta według mnie wygląda tak:
zad. 1
a) nie
b) nie
zad. 2
a) tak
b) nie
c) nie
d) tak
zad. 4
a) e^x
b) 25
c) 27x^26
d) -sin x
e) (-1)/(sin^2 x)
f) 5^x ln5
g) 1/(x lnpi)
h) (ln2)/(2^x)
Cześć
Z dzisiejszej lekcji nie rozumiem, skąd w zadaniu 3 wzięło się -q/x^2? A następne moje pytanie czy w przykładzie g) w zadaniu ostatnim można zostawić 1/2^xln przy podstawie 1/2? Jeśli nie to w jaki sposób to obliczyć lub uprościć?