Nagranie 3
Praca domowa:
Zad 1.
Oblicz pochodną
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Zad 2.
Oblicz pochodną
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Zad 3.
Oblicz pochodną
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Zad 4.
Oblicz pochodną
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Zad 5.
Oblicz pochodną
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Zad 6.
Podaj przykład funkcji f spełniającej podany warunek. Ile mozna podać takich funkcji?
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Zad 7.
Oblicz pochodną
a) ![]()
b) ![]()
c) ![]()
d) ![]()
rozwiązania Kliknij, aby zobaczyć rozwiązania









Bardzo dziękuję. To nagranie mi pomogło. Teraz już chyba bez problemu będę liczyć pochodne.
Oto moje rozwiązanie pracy domowej:
Zad. 1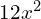
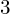
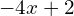
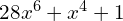
a)
b)
c)
d)
Zad.2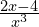
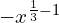
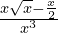
a) nie wiem 🙁
b)
c)
d)
Zad. 3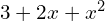
![Rendered by QuickLaTeX.com 3x^2+\frac{\sqrt[5]{x}}{x}+(x^3+2\sqrt{x})\cdot\frac{x^{\frac{1}{3}-1}}{3}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-fa35adeba214398a106759a2d68db320_l3.png)
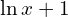
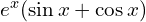
a)
b)
c)
d)
Zad. 4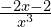
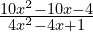
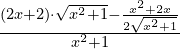
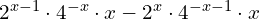
a)
b)
c)
d)
Zad. 5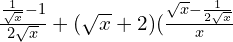
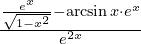
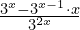
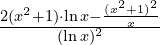
a)
b)
c)
d)
Co do zad. 6, to nie wiem, jak go rozwiązać, ponieważ mam dopiero 11 lat. Może dałby mi Pan jakąś wskazówkę? Wiem, że chodzi o szukanie tzw. funkcji pierwotnej i całkowanie. Jeden podpunkt umiem rozwiązać:![Rendered by QuickLaTeX.com -\cos x [\tex] Zad. 7 a) [tex] -3\sin x\cdot\arcsin x+\frac{3\cos x}{\sqrt{1-x^2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-23b63d47eeb6eef74de57356e080ffb9_l3.png)
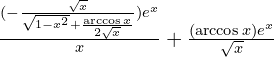
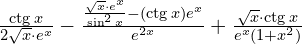
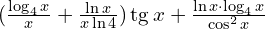
d)
b)
c)
d)
Jeżeli ten tekst nie został zamieniony na tekst do odczytu, proszę go skopiować do LaTeX’ a, a znaki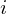 zamienić na $.
zamienić na $.
Wzory można pisać używając składni Latex, którą trzeba wstawić pomiędzy znaczniki
np. napisanie
[tex]f^{\prime}(x)=(x^2)^{\prime}=2x [/tex]spowoduje powstanie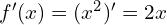 .
.
Ostatnim razem pomyliłem się w kwesti znacznika zamykające dalego nie działało sorry.