Macierze
Do czego służą macierze?
Pierwsze co przychodzi do głowy do łatwego zapisywania układów równań LINIOWYCH, czyli np. taki układ
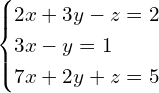
można zapisać tak
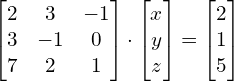
Tak na marginesie. W drugim równaniu nie było ![]() . Czyli inaczej
. Czyli inaczej ![]() zostało przemnożone przez
zostało przemnożone przez ![]() .
.
Pojawiło się słowo liniowych, co oznacza, że te wszystkie niewiadome nie miały żadnych potęg pierwiastków i innych takich, więc dla kontrastu zobacz przykład układu NIELINIOWEGO
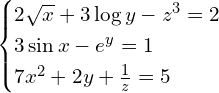
tego przy użyciu macierzy nie zapiszemy.
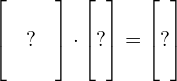
To co tu widzisz potraktuj na razie jako zajawkę. Będziemy to dalej dokładnie omawiać.
Czy to tylko jest tak sztuka dla sztuki.
Oczywiście, że nie. Macierz może reprezentować obrót punktu w układzie współrzędnych. np. obrót punktu ![]() o współrzędnych
o współrzędnych ![]() o kąt 30 stopni da nam nowy, którego współrzędne to
o kąt 30 stopni da nam nowy, którego współrzędne to
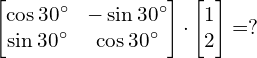
Całkiem możliwe że już intuicyjnie domyślasz jak to obliczyć. Jak nie wiesz to się nie przejmuj, wszystko jest okej. Dojdziemy do tego w swoim czasie.
Oczywiście takie same rzeczy można robić w przestrzeni 3D.
Podobnie można używać macierz do wykonywania przesunięć.
Przesunięcie wspomnianego punktu o wektor ![]() to:
to:
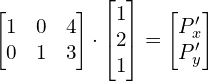 , albo w konwencji częściej spotykanej jak tu
, albo w konwencji częściej spotykanej jak tu
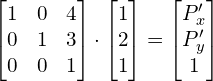
Przy pomocy Macierz można zapisać także liczbę zespoloną, albo kwaternion.
W robotyce do przejścia pomiędzy kolejnymi układami współrzędnych. O czym poniekąd było już przed chwilą. Macierze pozwalają także na dokonywanie rzutowań. By znać sposób przeliczenia punktów między widokiem, gdy patrzymy od przodu frontu na coś na widok, gdy patrzymy pod kątem i w drugą stronę.
W pakietach obliczeniowych są często używane do przechowywania dużej liczby liczb, które są w jakiś sposób ze sobą związane i/lub ułożone w pewnym porządku np. nagranie audio stereo w postaci cyfrowej
to będzie jakaś macierz np. 2 na 45000, gdzie pierwszym wymiarem wybieramy kanał lewy/ prawy, a drugim wymiarem “dźwięk” w danej chwili czasu.
Obraz cyfrowy w komputerze to też nic innego jak macierz. Obecna konfiguracja pikseli na ekranie komputera to macierz np. 1280 na 800 pikseli, gdzie w każdej pozycji znajduje się liczba mówiąca o intensywności świecenia danego piksela. W zasadzie to 3 takie macierze, o ile mówimy o obrazie kolorowym. Każda macierz odpowiada za jedną ze składowych koloru obrazu, czerwonego, zielonego i niebieskiego.
Trzeba to traktować bardziej jak narzędzie, które może być pomocne przy zapisie lub reprezentacji czegoś.
Przejdźmy do podejścia do tematu od strony bardziej formalnej.
1. Co to jest macierz?
Macierz to pewien uporządkowany układ liczb. W macierz nie zawsze muszą być liczb, ale nie komplikujmy już na samym początku. Układ rozmieszczenia tych liczb jest dwuwymiarowy, “płaski”. Poniżej przykłady pewnych macierzy.
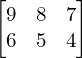

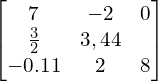
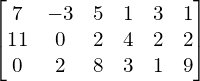
![]()
![]()
Czasami możesz spotkać macierz zapisywane przy mocy okrągłych nawiasów.
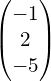
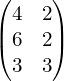
To tylko kwestia gustu. W Polsce przeważa zapis przy pomocy kwadratowych nawiasów. W literaturze anglojęzycznej często spotykamy nawiasy okrągłe.
2. Jak oznaczamy macierze?
Macierz zwyczajowo oznaczamy przez dużą pogrubioną literę. W piśmie ręcznym często z wygody się rezygnuje z pogrubiania.
np.
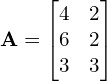
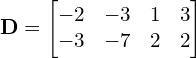
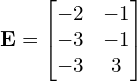
Oczywiście można tworzyć wyrażenia algebraiczne z tych liter np. ![]() , lecz trzeba uważać bo nie zawsze ma to sens. O tym w swoim czasie, nie wszystko na raz.
, lecz trzeba uważać bo nie zawsze ma to sens. O tym w swoim czasie, nie wszystko na raz.
3. Wymiary macierzy i jej stopień macierzy
Każda macierz ma dwa wymiary. Jeden mówiący o liczbie wierszy i drugi mówiący o liczbie kolumn.
Przykładowo ta macierz
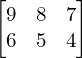
ma 2 wiersze i 3 kolumny, a poniższa
![]()
ma 3 wiersze i 1 kolumnę.
Jeżeli liczba wierszy jest równa liczbie kolumn to jest to macierz kwadratowa. Wówczas, tę liczbę kolumn, która jest równa liczbie wierszy nazywamy stopniem macierz. Jak widać mówienie o stopniu macierz ma sens tylko dla macierz kwadratowych.
np.

ma stopień równy 4.
4. Jak Wskazać konkretną liczbę w macierzy?
Czyli inaczej jak opisuje się jej położenie w macierzy.
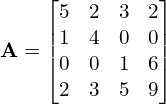
np. ![]() oznacza wybranie z macierz
oznacza wybranie z macierz ![]() elementu w 2 wierszu i w 3 kolumnie, czyli jest to
elementu w 2 wierszu i w 3 kolumnie, czyli jest to ![]()
![]()
Ogólniej indeksacja przebiega w ten sposób.
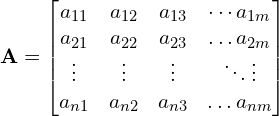
Jest macierzą stopnia n na m, co można zapisać w taki sposób ![]() , albo taki
, albo taki ![]() , czy np. tak
, czy np. tak ![]() oczywiście wszystko kwestia gustu, bo to tylko zapis, oznaczenie.
oczywiście wszystko kwestia gustu, bo to tylko zapis, oznaczenie.
5. Kiedy macierz jest wektorem
Macierz, w której z jeden z wymiarów jest równy 1 nazywamy wektorem.
np.
![]()
![]()
![]()
![]()
6. Dodawanie macierzy
Dodawać można macierze tylko o tych samych rozmiarach. Aby dodać macierz ![]() do macierz
do macierz ![]() to liczba wierszy macierz A musi być równa liczbie wierszy macierz B oraz liczba kolumn macierzy A musi być równa liczbie wierszy macierz B np.
to liczba wierszy macierz A musi być równa liczbie wierszy macierz B oraz liczba kolumn macierzy A musi być równa liczbie wierszy macierz B np.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 2 & 2 \\ 9 & 2 \end{bmatrix}+ \begin{bmatrix} -1 & -2 \\ 3 & 0 \end{bmatrix} = \begin{bmatrix} 2-1 & 2-2 \\ 9+3 & 2+0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 12 & 2 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f5c4ed0917a2f291208471ba3d459b39_l3.png)
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 1 & 0 & 2\\ 1 & 2 & 2 \end{bmatrix}+ \begin{bmatrix} 0 & 1 & 1\\ 2 & 3 & 1\end{bmatrix} = \begin{bmatrix} 1+0 & 0+1 & 2+1\\ 1+2 & 2+3 & 2+1 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 3 \\ 3 & 5 & 3 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-adca974e8f563c6bd023affff809bac6_l3.png)
Ogólnie można to zapisać jako:
![]()
![]()
Trzeba przyznać, że jest to dosyć intuicyjne.
DARMOWY WIDEO KURS:
Macierzy








