Month: grudzień 2012

Interpretacja wzoru Eulera (Euler’s formula)

Posted on by Mateusz Kowalski

Wzór Eulera wygląda następująco.

    \[ \boxed{e^{it}=\cos t + i \sin t} \]

Mamy tu porównanie liczby zespolonej w postaci wykładniczej

    $$z= |z| \cdot e^{i \arg z}$$

o module równym 1. Z reprezentacją algebraiczną

    $$z = a+bi $$

Mamy zatem

    $$ |z| \cdot e^{i \arg z}=a + bi$$

moduł liczby zespolonej to

    $$ |z| =\sqrt{a^2 + b^2}$$

Jeżeli przyjmiemy, że weźmiemy liczbę o module 1, czyli

    $$ a^2 + b^2=1$$

to uzyskamy:

    $$ e^{i \arg z} =a + bi$$

Wzór Eulera mówi, że w tym przypadku a i b musi być równe.

    $$ a= \cos(\arg z) $$

    $$ b=\sin(\arg z)$$

Poniżej prezentuje animacje w jasny sposób obrazująca cała tą tożsamość.
Wzór Eulera
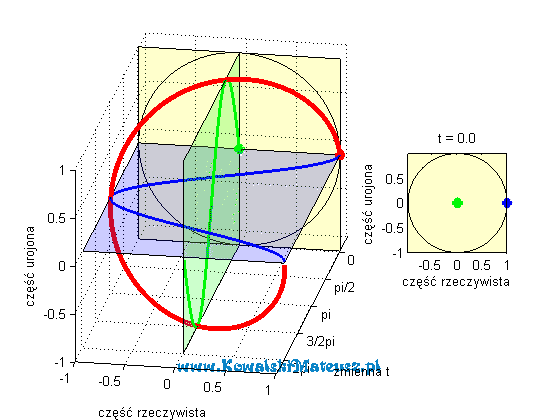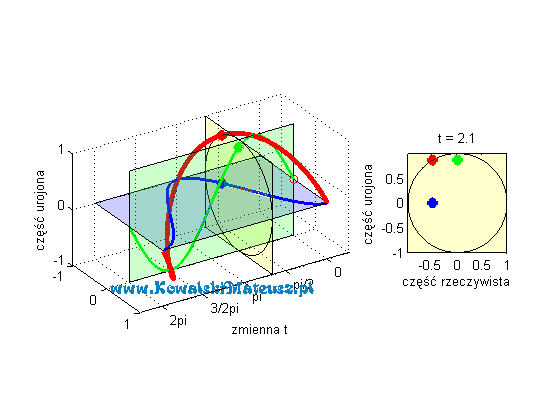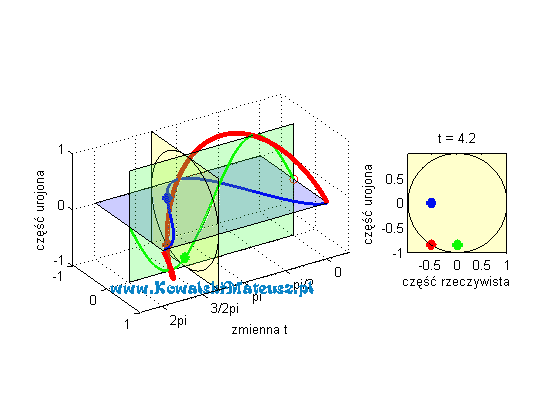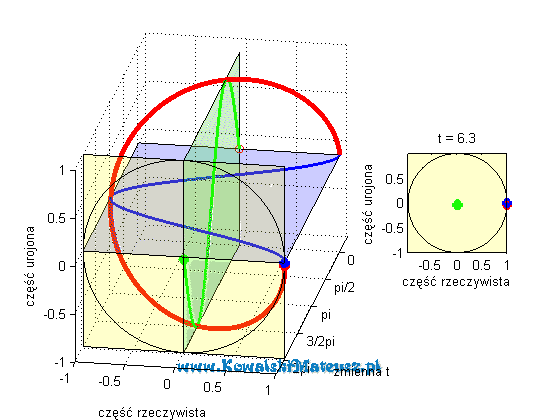
Continue reading →