Month: marzec 2013

Twierdzenie spektralne (Spectral theorem)

Posted on by Mateusz Kowalski

Opowiem Ci dziś o reprezentacji spektralnej lub jak kto woli Twierdzeniu spektralnym.
Z tym, że ograniczę się dla prostoty tylko do macierzy.

Pokaże Ci specjalną własność na przykładzie, a potem uogólnimy na szersze przypadki.

PRZYKŁAD 1.
Weźmy macierz, dla której zachodzi warunek \mathbf{A}{{\mathbf{A}}^{T}}={{\mathbf{A}}^{T}}\mathbf{A}. Macierz, która to spełnia nazywana jest to macierz normalną o współczynnikach rzeczywistych, ale do tego jeszcze dojdziemy. Masz zatem dla przykładu macierz

\mathbf{A}=\left[ \begin{matrix} 1 & 3 & 0 \\ 3 & -2 & -1 \\ 0 & -1 & 1 \\ \end{matrix} \right]

Tak na marginesie to jest jeszcze szczególniejszy przypadek macierz normalnej rzeczywistej, gdyż jest to macierz symetryczna. Czyli {{\mathbf{A}}^{T}}=\mathbf{A}

Wyliczasz wartości własne wychodzą takie 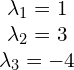\begin{matrix} {{\lambda }_{1}}=1 \\ {{\lambda }_{2}}=3 \\ {{\lambda }_{3}}=-4 \\ \end{matrix}, można to oczywiście zapisać tak \left\{ {{\lambda }_{i}} \right\}_{i=1}^{3}=\{1,3,-4\}. Widać także, że każda lambda jest jednokrotna.
Obliczasz odpowiadające tym wartości własnym wektory własne o normie równej 1, czyli unormowane (bardzo ważne). A następnie dla tych wektorów odpowiadające projektory.

{{\mathbf{V}}_{1}}=\left[ \begin{matrix} 1 \\ 0 \\ 3 \\ \end{matrix} \right]\frac{1}{\sqrt{10}}

    \[{{\mathbf{p}}_{1}}=\left[ \begin{matrix} 1 \\ 0 \\ 3 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} 1 & 0 & 3 \\ \end{matrix} \right]\cdot \frac{1}{10}=\left[ \begin{matrix} 1 & 0 & 3 \\ 0 & 0 & 0 \\ 3 & 0 & 9 \\ \end{matrix} \right]\cdot \frac{1}{10}\]

{{\mathbf{V}}_{2}}=\left[ \begin{matrix} 3 \\ 2 \\ -1 \\ \end{matrix} \right]\frac{1}{\sqrt{14}}

{{\mathbf{p}}_{2}}=\left[ \begin{matrix} 3 \\ 2 \\ -1 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} 3 & 2 & -1 \\ \end{matrix} \right]\cdot \frac{1}{14}=\left[ \begin{matrix} 9 & 6 & -3 \\ 6 & 4 & -2 \\ -3 & -2 & 1 \\ \end{matrix} \right]\cdot \frac{1}{14}

{{\mathbf{V}}_{3}}=\left[ \begin{matrix} -3 \\ 5 \\ 1 \\ \end{matrix} \right]\frac{1}{\sqrt{35}}

{{\mathbf{p}}_{2}}=\left[ \begin{matrix} -3 \\ 5 \\ 1 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} -3 & 5 & 1 \\ \end{matrix} \right]\cdot \frac{1}{35}=\left[ \begin{matrix} 9 & -15 & -3 \\ -15 & 25 & 5 \\ -3 & 5 & 1 \\ \end{matrix} \right]\cdot \frac{1}{35}

To co chcę Ci pokazać to że zajdzie taka równość: Continue reading →