Obiecywałem w poprzednich postach opowiedzieć o reszcie Lagrange’a tak też zrobię.
Zacznę od stwierdzenia, na którym zakończyłem parę wpisów wcześniej przy opisie wielomianów Taylora.
Wielomian Taylora wraz z resztą Lagrange’a daje wzór Taylora.
Kiedy rozwijamy funkcję w wielomian Taylora pewnego skończonego stopnia, powiedzmy do funkcji trzeciego stopnia, to reszta Lagrange’a będzie stopnia o 1 większym czyli 4.
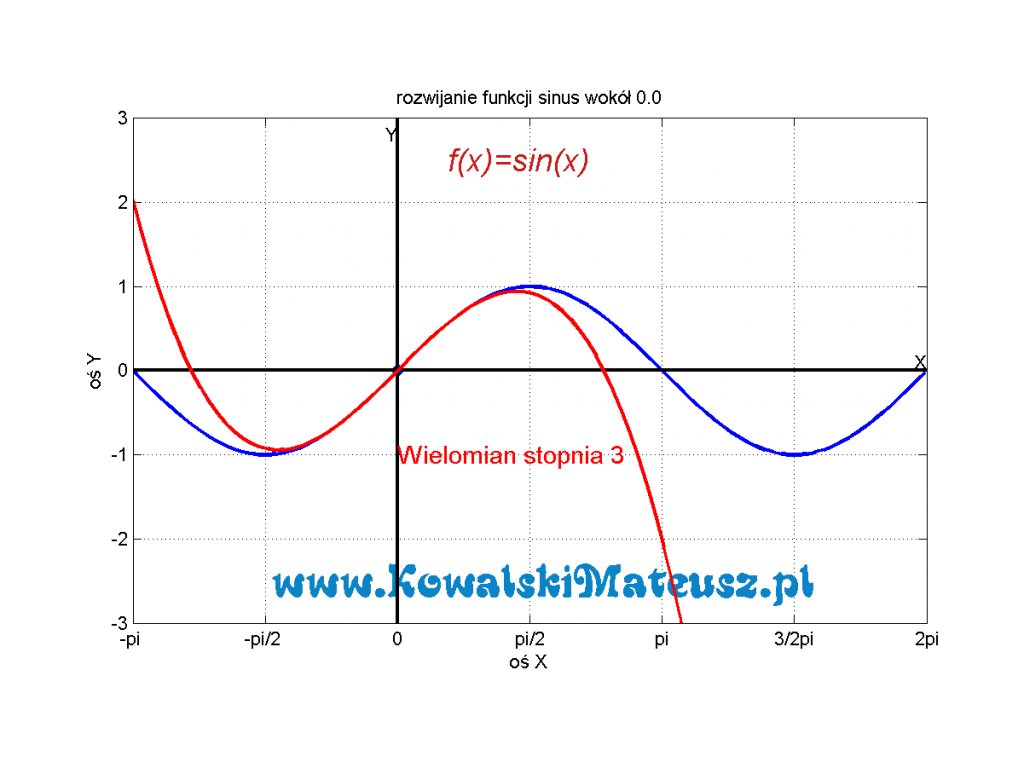
Weźmy funkcję sin x i rozwińmy ją w wielomian Taylora do stopnia 3 wokół punktu 
(czyli rozwinięcie Maclaurina). Rysunek prezentuje takie rozwinięcie.
Continue reading
