Month: wrzesień 2011

Twierdzenie o 2 Ciągach lub Funkcjach

Posted on by Mateusz Kowalski

Skoro ostatnio opowiadałem o twierdzeniu o trzech ciągach to teraz opowiem o twierdzeniu o 2 ciągach.

Jeśli ciąg b_n dla indeksów n>n_0 ma wartości mniejsze od wartości ciągu a_n oraz ciąg b_n jest rozbieżny do +\infty, to również ciąg, a_n musi być rozbieżny do +\infty.

Analogiczne twierdzenie dla funkcji zamiast dla ciągów również jest prawdziwe.

Twierdzenie o dwóch funkcjach

Graficzna interpretacja twierdzenia o 2 ciągach.

Twierdzenie o 3 ciągach lub funkcjach

Posted on by Mateusz Kowalski

Cóż to takiego. Brzmi co najmniej dziwnie. Jest to naprawdę bardzo proste twierdzenie tak proste, że aż się możesz zdziwić co w nim takiego odkrywczego.
A zatem do dzieła.

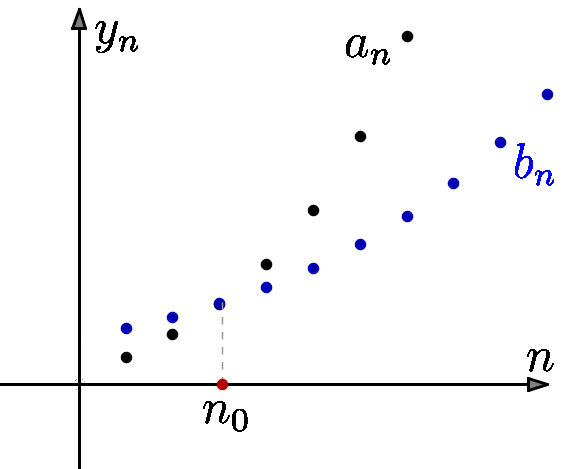
Mam bardzo dobry przykład obrazujący to twierdzenie. Wyobraź sobie dwóch policjantów i siebie. Teraz zobacz jak jeden z tych policjantów idzie na posterunek. Potem zwróć uwagę, że drugi policjant także idzie na posterunek. No a ty znajdujesz się cały czas między nimi i także sobie maszerujesz. Wniosek jest taki, że jeśli jesteś cały czas między dwoma policjantami i oni obaj zmierzają do posterunku to Ty także trafisz na posterunek.
Oto całe twierdzenie.

Twierdzenie o 3 ciągach

No dobrze ale do czego jest mi potrzebna taka oczywistość?

Już spieszę z odpowiedzią.
jak policzyć granicę tego ciągu

\lim\limits_{n\to\infty}\sqrt[n]{2^n+3^n+4^n}= \?

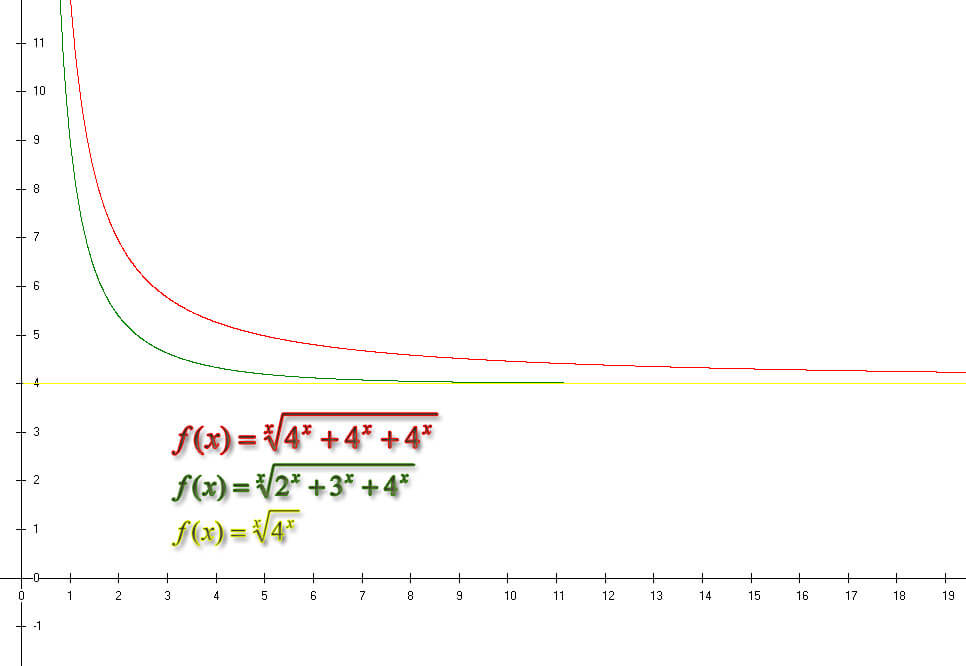
Możemy ograniczyć ciągiem większym i mniejszym

\sqrt[n]{4^n}\leqslant \sqrt[n]{2^n+3^n+4^n} \leqslant \sqrt[n]{4^n+4^n+4^n}

obliczając granicę jednego ciągu mamy

\lim\limits_{n\to\infty}\sqrt[n]{4^n}=4

Ale obliczając granicę drugiego ciągu mamy

\lim\limits_{n\to\infty}\sqrt[n]{4^n+4^n+4^n}=\lim_{n\to\infty}\sqrt[n]{3}\cdot\sqrt[n]{4^n}=1\cdot4=4

A zatem granica naszego szukanego ciągu wynosi

\lim\limits_{n\to\infty}\sqrt[n]{2^n+3^n+4^n}=4

Na mocy twierdzenia o 3 ciągach.
Twierdzenie o 3 ciągach

Coś na temat szachów

Posted on by Mateusz Kowalski

Legendę o Twórcy szachów można zobaczyć tu:



liczba ziaren, które zażyczył sobie twórca oblicza się następująco
szachownica ma 8 na 8 pól czyli 64 pola suma ziaren wynosi.

\\ S=\underbrace{1+2+4+8+16+...}_{i \ tak \ 64 \ razy}

\\ S=2^0+2^1+2^2+2^3+...+2^{62}+2^{63}

Jest to ciąg geometryczny o ilorazie q=2 tzn, że każde następne pole ma 2 razy więcej ziaren niż poprzednie.

Wzór jest następujący S_{n}=a_{1}\cdot\frac{1-q^n}{1-q}

U nas n=64, bo tyle jest pól szachownicy.
Pierwszy wyraz wynosi a_1=1.
Podstawiając do wzoru mamy, że suma wszystkich ziaren równa jest

S_{64}=1\cdot\frac{1-2^{64}}{1-2}=2^{64}-1

Ta liczba wygląda dosyć nie pozornie jednak wynosi dokładnie

2^{64}-1=18446744073709551620
chcą sobie uzmysłowić jak wielka jest to liczba
zróbmy tak

2^{64}-1\approx2^{60}={2^{30}}^{2}\approx1000000000\cdot1000000000

Miliard razy miliard to tak jakby do każdego ziarna z miliarda dołożyć miliard ziaren i nadal nie będzie to w pełni ta liczba.