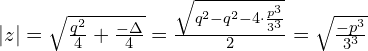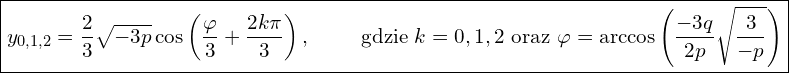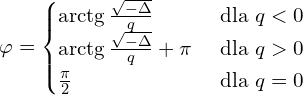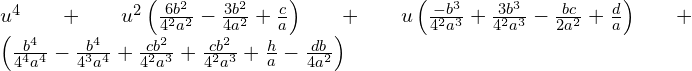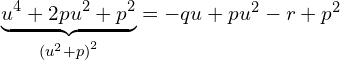Zacznijmy od najprostszego.
Równanie pierwszego stopnia (liniowe)
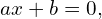
gdzie
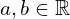
oraz
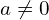
Filozofii to tu nie ma
 Równanie drugiego stopnia (kwadratowe)
Równanie drugiego stopnia (kwadratowe)
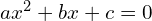
gdzie
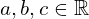
oraz
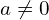
są dwa rozwiązania
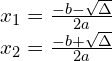
gdzie
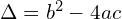 Równanie trzeciego stopnia (sześcienne)
Równanie trzeciego stopnia (sześcienne)
tu nie będzie już tak łatwo
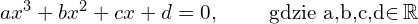
gdzie
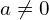
, bo jeśli
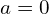
to nie jest to równanie sześcienne.
Najpierw podzielmy przez 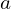 , aby mieć
, aby mieć 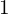 przy najwyższej potędze niewiadomej.
przy najwyższej potędze niewiadomej.
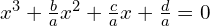
Zauważmy, iż równanie można sprowadza się do równania postaci, w której nie ma składnika z niewiadomą w kwadracie
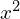
. Wystarczy podstawić za niewiadomą
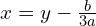
nową niewiadomą
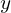
.
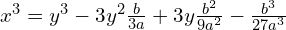
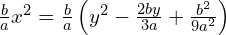
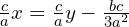
łącząc i grupując ze względu na potęgi
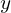
otrzymamy:
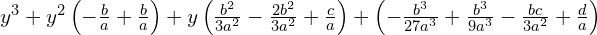
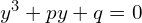
gdzie:
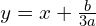
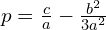
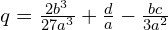
Mamy teraz do rozpatrzenia prostsze równanie 3 stopnia w postaci kanonicznej, z niewiadomą 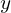 .
.
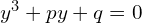
Nikt nie zabronić tej niewiadomej przedstawić w postaci sumy dwóch innych niewiadomych wielkości.
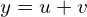
Wówczas
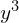
jest równe
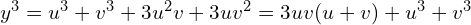
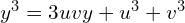
Przekształcając równanie mamy
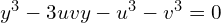
Równanie to ma taką samą postać jak nasze wejściowe kanoniczne, czyli
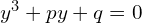
Można zatem utożsamić te równania ze sobą, a co za tym idzie wielkości
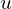
i
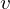
z danymi współczynnikami
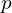
i
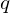
.
Po co to robimy, bo 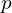 i
i 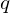 jest znane, ponieważ są zdeterminowane przez
jest znane, ponieważ są zdeterminowane przez 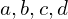 , które znamy. Natomiast kombinacja
, które znamy. Natomiast kombinacja 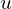 i
i 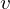 to jest nasza niewiadomą, którą chcemy znaleźć, więc naszym celem jest “tylko” wyrazić
to jest nasza niewiadomą, którą chcemy znaleźć, więc naszym celem jest “tylko” wyrazić 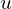 i
i 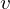 od tych znanych wielkości.
od tych znanych wielkości.
Co sprowadza się do układu równań.
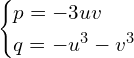
Z pierwszego równania mamy 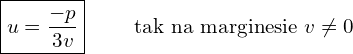
Wstawiamy do drugiego równania. 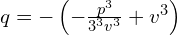
Mnożąc obustronnie przez 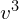
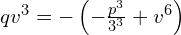 mamy równianie trikwadratowe, które sprowadzamy do równania kwadratowego poprzez podstawienie
mamy równianie trikwadratowe, które sprowadzamy do równania kwadratowego poprzez podstawienie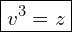 Przez to, że
Przez to, że 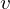 jest nieznane to teraz nową nieznaną jest
jest nieznane to teraz nową nieznaną jest 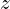
Zagadnienie sprawdziliśmy do równania kwadratowego postaci
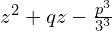
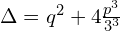
Teraz bardzo ważne z delty będziemy liczyć pierwiastek, więc musimy


Skoro znamy
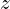
, to chcemy wrócić do
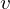
.

TERAZ UWAGA
Mamy niewiadomą w 3 potędze która jest równa liczbie rzeczywistej. Mamy więc 1 rozwiązanie rzeczywiste i 2 zespolone. Z pierwszym nie ma problemu, bo wystarczy tylko
![Rendered by QuickLaTeX.com v = \sqrt[3]{ \frac{-q \pm \sqrt{\Delta}}{2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bb815576e4c1ea222f0f632d127b95bf_l3.png)
. Natomiast aby znaleźć pozostałe to dobrze wykorzystać pierwiastki z jedynki.
Przypominamy, że jeśli mamy równanie 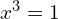 to
to
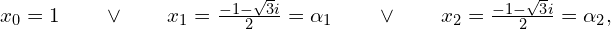
gdzie
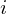
jest jednostką urojoną także, że
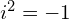
. Ile
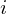
jest równe? To jest dobre pytanie i od razu zaznaczam.
![Rendered by QuickLaTeX.com \[\R{i \neq \sqrt{-1} },\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ea3f72545f99dd02ad67f3c92bc4028e_l3.png)
choć wiele osób tak uczy to jest to jawne nadużycie. Czym wówczas były by 3 różne jednostki urojone w kwaternionach, gdzie każda jest inna, oraz kwadrat każdej daje 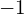 . Zostawmy to, jednak bo to inny temat i wróćmy do zadania.
. Zostawmy to, jednak bo to inny temat i wróćmy do zadania.
Warto przy tym zdać sobie sprawę z
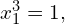
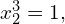
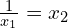 oraz
oraz
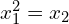 jaki i
jaki i
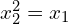
Takie to ciekawe liczby, choć nie rzeczywiste to bardzo przydatne.
Wykorzystujac ten fakt łatwo rozwiąząć np. 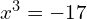
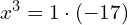
![Rendered by QuickLaTeX.com x_0 = \sqrt[3]{1}\sqrt[3]{17} = 1\cdot \sqrt[3]{17} = \sqrt[3]{17}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-61cd5d520108bd17aea94b655d05edf0_l3.png)
![Rendered by QuickLaTeX.com x_1 = \frac{-1-\sqrt{3}i}{2} \cdot \sqrt[3]{17}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-7dad579fa1ea39ecfb58273834e66a98_l3.png)
![Rendered by QuickLaTeX.com x_2 = \frac{-1+\sqrt{3}i}{2} \cdot \sqrt[3]{17}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-43c482362eda80cf709b6c52cf3ef558_l3.png)
Kończąc dygresję, u nas będzie.
![Rendered by QuickLaTeX.com v_1 = v = \sqrt[3]{ \frac{-q \pm \sqrt{\Delta}}{2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4c2d1c35f0ea2b66fb7f1e8bd1d69919_l3.png)
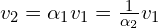
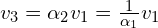
Gdy znamy 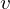 to wracamy do
to wracamy do 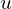 . Wyznaczyliśmy wcześniej, że
. Wyznaczyliśmy wcześniej, że 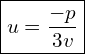
Zobaczmy ile wynosi 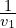
![Rendered by QuickLaTeX.com \frac{1}{v_1} = \sqrt[3]{\frac{-2}{q\R{\mp} \sqrt{\Delta}}}=\sqrt[3]{\frac{-2(q\pm \sqrt{\Delta})}{q^2-\Delta}}= \sqrt[3]{\frac{q\pm \sqrt{\Delta}}{2 \frac{p^3}{3^3}}}=\frac{3}{p}\sqrt[3]{\frac{-q\R{\mp} \sqrt{\Delta}}{2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a9fb080d45947c9a90eada60d0e53698_l3.png)
Wymiemy ile teraz wynosi 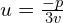
![Rendered by QuickLaTeX.com u_1 = \sqrt[3]{ \frac{-q \R{\mp} \sqrt{\Delta}}{2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3ad35f48125ba8668d42e046ba305215_l3.png)
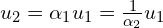
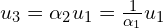
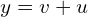
Puki co wydawać by się mogło że mamy 6 potencialnych rozwiązań bo jeszcze dowolność znaku 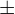 . Jednak okazuje się, że rozwiązań może być co najwyżej 3, bo
. Jednak okazuje się, że rozwiązań może być co najwyżej 3, bo
![Rendered by QuickLaTeX.com y_1 = \sqrt[3]{ -\frac{q}{2} \R{\pm} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \sqrt[3]{ -\frac{q}{2} \R{\mp} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-77028c471831154b8bf239ca6652066e_l3.png)
oznacza
![Rendered by QuickLaTeX.com y_1 = \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d59ed2565c3503e381306e230d227176_l3.png)
lub
![Rendered by QuickLaTeX.com y_1 = \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0b75397f828173191c336e4b510fba7d_l3.png)
a to jest to samo.
Mamy zatem końcowe wzory dla przypadku 
————————————————————————–
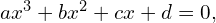
![Rendered by QuickLaTeX.com y_1 = \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d59ed2565c3503e381306e230d227176_l3.png)
![Rendered by QuickLaTeX.com y_2 = \frac{-1\R{-}\sqrt{3}i}{2} \cdot \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \frac{-1\R{+}\sqrt{3}i}{2}\cdot \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-271f2908955ad1c0e7936ae3c18feb7c_l3.png)
![Rendered by QuickLaTeX.com y_3 = \frac{-1\R{+}\sqrt{3}i}{2} \cdot \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \frac{-1\R{-}\sqrt{3}i}{2}\cdot \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a302c430366fd21549cd1a50bb3f606a_l3.png)
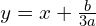
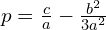
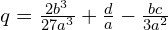
————————————————————————–
Warto się jeszcze zastanowić Czy 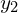 i
i 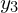 mogą być kiedyś rzeczywiste okazuje się, że jest to możliwe tylko, gdy
mogą być kiedyś rzeczywiste okazuje się, że jest to możliwe tylko, gdy 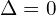 i wówczas
i wówczas 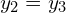 i będzie to podwójny rzeczywisty pierwiastek, i innej opcji nie ma.
i będzie to podwójny rzeczywisty pierwiastek, i innej opcji nie ma.
Spójrzmy na 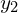
![Rendered by QuickLaTeX.com \G{y_2} = \frac{\G{-1}\R{-}\sqrt{3}i}{2} \cdot \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \frac{\G{-1}\R{+}\sqrt{3}i}{2}\cdot \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4ae0dc26ea7cd7161e899eda9bdeb090_l3.png)
Aby cześć urojona się wyzerował to
![Rendered by QuickLaTeX.com \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} = \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-544633da9a9dd43ac0d23048b2bd5cfc_l3.png) ,
,
a to jest możliwe tylko gdy 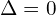
Analogicznie dla
![Rendered by QuickLaTeX.com \G{y_3} = \frac{\G{-1}\R{+}\sqrt{3}i}{2} \cdot \sqrt[3]{ -\frac{q}{2} \R{+} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }} + \frac{\G{-1}\R{-}\sqrt{3}i}{2}\cdot \sqrt[3]{ -\frac{q}{2} \R{-} \sqrt{\frac{q^2}{4}+\frac{p^3}{27} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ff07a3ec033550aa09c294891d34ebe5_l3.png)
wówczas
![Rendered by QuickLaTeX.com \boxed{ y_0 = 2\sqrt[3]{-\frac{q}{2}}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3dc08c0b58315bcd86559c26ade95af1_l3.png)
![Rendered by QuickLaTeX.com \boxed{y_1=y_2 = -\sqrt[3]{-\frac{q}{2}}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-dfe70a705a2a572fb3c914027b86f7b8_l3.png)
Jeśli
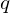
jest równe
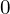
to wówczas mamy potrójny pierwiastek
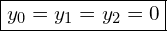
Przejdźmy do sytuacji, gdy  . Tutaj sprawa wygląda nieco inaczej.
. Tutaj sprawa wygląda nieco inaczej.
Pierwszy wniosek na marginesie 
Chcąc spierwiastkować liczbę ujemną musimy jej zmienić znak, aby była teraz dodatnia i można było ja spierwiastkować, a tę zmianę korygujemy przemnażając wynik przez 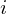 , wówczas:
, wówczas:
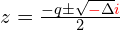
Teraz mamy do spierwiastkowania 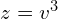 liczbę zespoloną, a nie rzeczywistą, więc “trick” z pierwiastkami z jedynki nie zadziała.
liczbę zespoloną, a nie rzeczywistą, więc “trick” z pierwiastkami z jedynki nie zadziała.
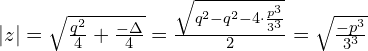
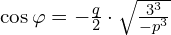
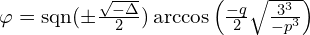
![Rendered by QuickLaTeX.com v_{0,1,2} = \sqrt[3]{\sqrt{\frac{-p^3}{3^3}}}\left[ \cos\left( \frac{\varphi+2k\pi}{3} \right) + i\sin\left( \frac{\varphi+2k\pi}{3} \right) \right] \qquad \mbox{ dla } k=0,1,2](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-76f4aafa59b09395b852b23154193ece_l3.png)
ponieważ 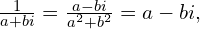 bo
bo 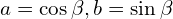
![Rendered by QuickLaTeX.com u_{0,1,2} = \sqrt[3]{\sqrt{\frac{-p^3}{3^3}}}\left[ \cos\left( \frac{\varphi+2k\pi}{3} \right) \R{-} i\sin\left( \frac{\varphi+2k\pi}{3} \right) \right] \qquad \mbox{ dla } k=0,1,2](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-08921070deb74d131abab2d4441bcc2e_l3.png)
dodając 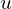 i
i 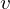 powstają końcowe wzory.
powstają końcowe wzory.
Warto spostrzec że znak kąta 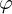 nie ma znaczenia dla kosinusa, więc można pominąć
nie ma znaczenia dla kosinusa, więc można pominąć 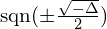 , ponieważ
, ponieważ 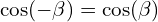 , czyli w naszym przypadku
, czyli w naszym przypadku
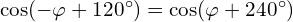 jaki i
jaki i
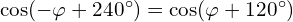
Mamy zatem końcowe wzory dla przypadku 
————————————————————
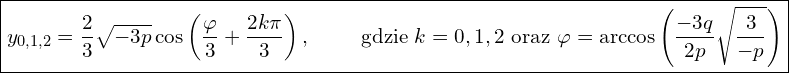
————————————————————-
Zauważ, że w tym wypadku wszystkie 3 rozwiązania są rzeczywiste
Warto przekonać się, iż rozwiązaniem równania
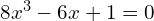
jest
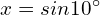
PODSUMOWANIE ALGORYTM DLA KOMPUTERA ROZWIĄZANIA OGÓLNEGO RÓWNANIA O WSPÓŁCZYNNIKACH RZECZYWISTYCH
Aby rozwiązać
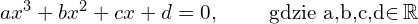
Obliczmy
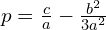
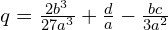
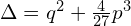
if 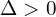 to
to
![Rendered by QuickLaTeX.com y_0 = \sqrt[3]{ -\frac{q}{2} \R{+} \frac{\sqrt{\Delta}}{2} }} + \sqrt[3]{ -\frac{q}{2} \R{-} \frac{\sqrt{\Delta}}{2} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3668cb06d83f5484da5aa0e436474eb7_l3.png)
else if 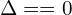 UWAGA NA DOKŁADNOŚĆ KOMPUTEROWYCH OBLICZEŃ PORÓWNANIA Warto dla
UWAGA NA DOKŁADNOŚĆ KOMPUTEROWYCH OBLICZEŃ PORÓWNANIA Warto dla 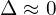 lepiej badać
lepiej badać 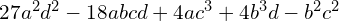 , które jest przemnożeniem delty przez
, które jest przemnożeniem delty przez 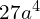 i korzystamy tu ze źródłowych danych
i korzystamy tu ze źródłowych danych 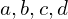
![Rendered by QuickLaTeX.com y_0 = 2\sqrt[3]{ -\frac{q}{2} }}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-521252f17b43d27933cc832ad29c7301_l3.png)
![Rendered by QuickLaTeX.com y_{1,2} = \R{-}\sqrt[3]{ -\frac{q}{2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-46cb0bb8b5e34cd39f019bfd8b5d17ee_l3.png)
else if to
to
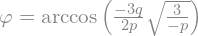 słaby ze względu na nie dokładności numeryczne, może powodować dla kątów bliskich
słaby ze względu na nie dokładności numeryczne, może powodować dla kątów bliskich 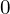 i
i 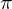 , czyli gdy
, czyli gdy 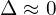 zwielokrotnienie błędu niedokładności.
zwielokrotnienie błędu niedokładności.
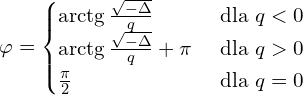
Uwaga na 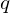 bliskie zeru, wówczas lepiej użyć wzoru szarego na
bliskie zeru, wówczas lepiej użyć wzoru szarego na 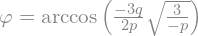 . Ponadto jeśli
. Ponadto jeśli 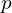 i
i 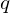 są bliskie
są bliskie 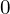 , a to ma miejsce przy dużym
, a to ma miejsce przy dużym 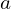 to wówczas lepiej wzoru, bazującego na źródłowych danych
to wówczas lepiej wzoru, bazującego na źródłowych danych 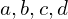 czyli po przekształceniu
czyli po przekształceniu ![Rendered by QuickLaTeX.com \varphi = \arccos \left( 6b^3\sqrt[3]{\frac{a^2}{b^2-3ac}} \right)](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0febfda512853afd426ec533de66a23f_l3.png)
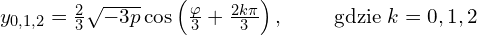
end
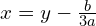
Równanie czwartego stopnia
Tu będzie jeszcze trudniej, ale jeszcze można.
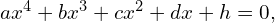
gdzie
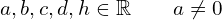
Zamieniajmy niewiadomą
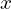
na niewiadomą
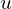
w taki sposób.
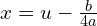
Skorzystajmy ze wzoru skróconego mnożenia.
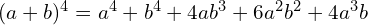
Zróbmy rachunki pomocnicze
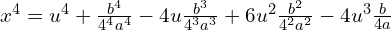
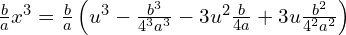
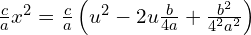
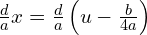
Podstawiamy do równania i uprośćmy
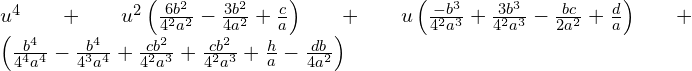
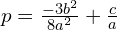
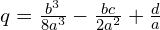
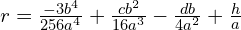

Dodając z lewej i prawej strony równania 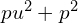
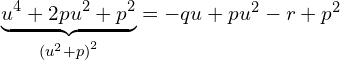
Teraz dodając z lewej i prawej strony pewną niewiadomą wartość 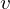 , a dokładniej
, a dokładniej 
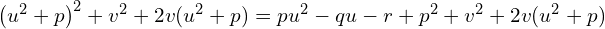
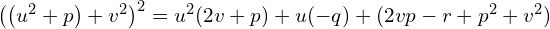
Z lewej strony równania mam kwadrat to z prawej też musi być kwadrat, aby równianie było prawdziwe. Skoro tak to z prawej strony musi być 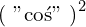 , czyli podwójny pierwiastek, więc
, czyli podwójny pierwiastek, więc  równania kwadratowego
równania kwadratowego 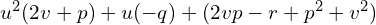 ze względu na
ze względu na 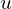 , (bo
, (bo 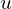 jest niewiadomą), po prawej stronie musi być równa
jest niewiadomą), po prawej stronie musi być równa 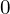
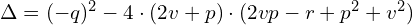
czyli 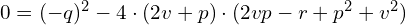
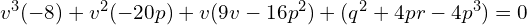
Chcąc znaleźć niewiadomą
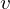
, dla której ten warunek, czyli to równianie będzie spełnione musimy rozwiązać równie
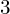
stopnia ze względu na
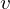
Po znalezieniu rozwiązań, których liczba to 1, 2 lub 3, znamy wartość 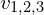
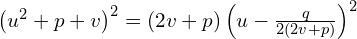
ponieważ trójmian kwadratowy z deltą równą 0 można zapisać tak 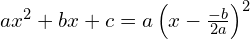
Przekształcając i odejmując obustronie prawą stronę otrzymamy
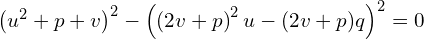
Mamy tutaj różnicę dwóch kwadratów 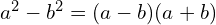 , czyli
, czyli
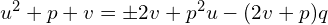
Teraz aby znaleźć 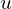 , bo
, bo 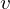 już znamy trzeba rozwiązać równie kwadratowe.
już znamy trzeba rozwiązać równie kwadratowe.
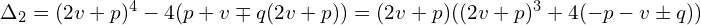

W związku z tym, że znak dodania lub odjęcia 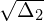 nie jest zależy od wyboru pozostałych znaków, to dla porządku oznaczyłem go przez
nie jest zależy od wyboru pozostałych znaków, to dla porządku oznaczyłem go przez 
Wydawać by się mogło, że mamy zatem aż 2 razy 2 razy 3 czyli 12 kandydatów na rozwiązanie ogólnego równania 4 stopnia. Natomiast w ogólnej sytuacji mamy 8 możliwych opcji.
1) brak rozwiązań
2) 1 rozwiązanie podwójne
3) 2 rozwiązania pojedyncze
4) 2 rozwiązania podwójne
5) 2 rozwiązania pojedyncze i 1 podwójne
6) 1 rozwiązanie pojedyncze i 1 potrójne
7) 4 pojedyncze
8) 1 rozwiązanie poczwórne
Choć ze względu na liczbę pierwiastków licząc także krotność to mamy albo 0 pierwiastków albo 2 albo 4.
Równanie piątego stopnia i wyższych
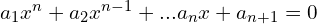
gdzie
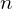
to stopień równania
“Problem rozwiązalności takich równań badany był od końca XVI wieku, gdy matematycy włoscy podali wzory na rozwiązania równań stopni 3 i 4. Zmagali się z nim Bézout, Euler i Lagrange, jednak dopiero Paolo Ruffini wpadł na pomysł, by udowodnić, że w przypadku równań stopnia wyższego niż 4 odpowiednie wzory nie istnieją. Opublikowany przez niego w roku 1799 dowód twierdzenia (Ruffini podał pięć dowodów) zawierał pewne nieścisłości i został zignorowany przez społeczność matematyków – być może przyczyną był fakt, że Ruffini był także lekarzem. W pełni zadowalający dowód opublikował w roku 1824 Niels Henrik Abel, został on następnie uproszczony w roku 1845 przez Pierre’a Wantzela. Jednak znacznie głębsza analiza problemu zawarta jest w pracach Évariste’a Galois pod postacią teorii Galois.” źródło
Wikipedia
źródła:
Matematyka.pl
Wikipedia
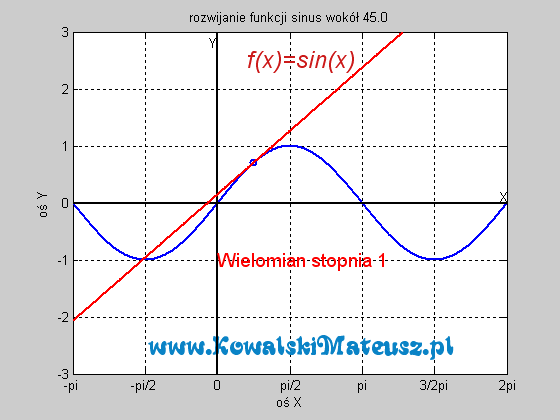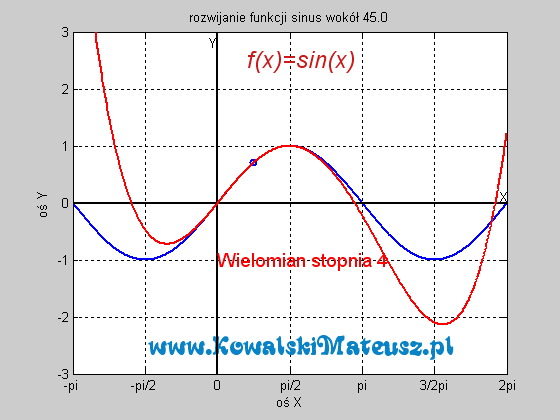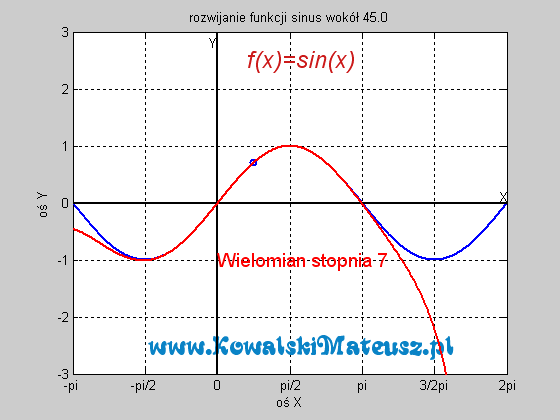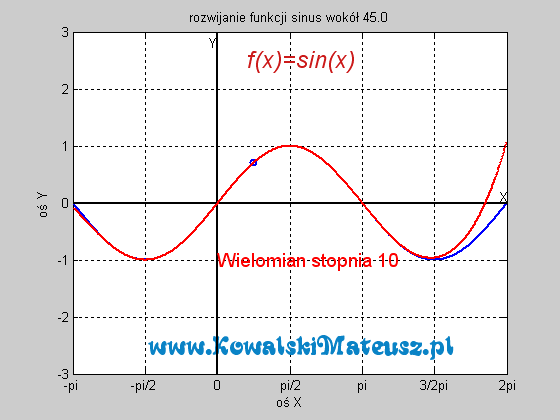
![]()
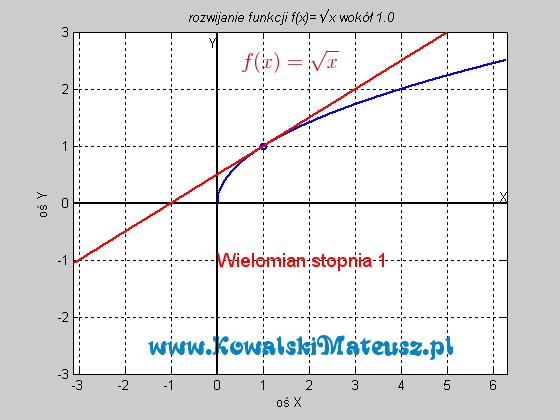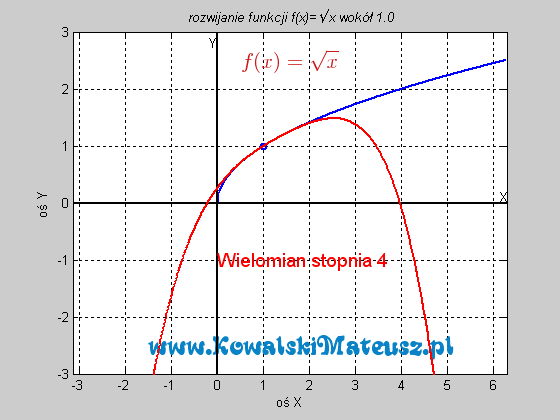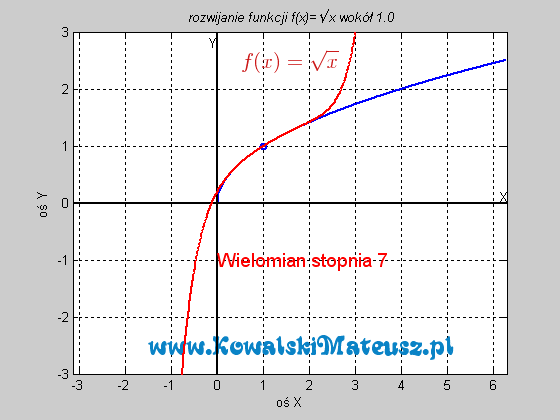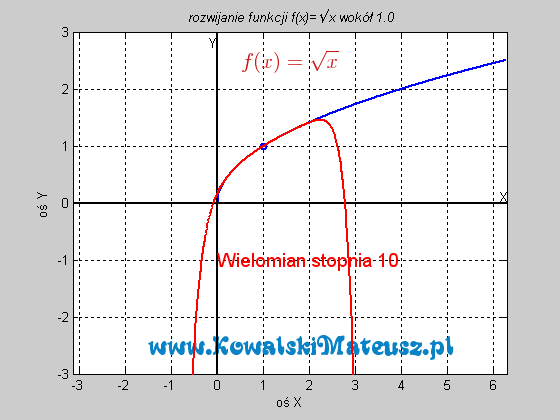
![]() . Ciekawe skąd ten twór to wiedział. Czy nie zastanawiałeś się skąd kalkulator to wie? Ten wzór po prostu sprowadza problem znajdowania sinusa do problemu dodawań, mnożeń i dzieleń, a te już potrafi wykonać. Wyprzedzając pytanie a jak potrafi dodawać. Kręci mnie, żeby wejść w temat techniki cyfrowej i to wytłumaczyć, ale na to bym musiał poświęcić osobny blog.
. Ciekawe skąd ten twór to wiedział. Czy nie zastanawiałeś się skąd kalkulator to wie? Ten wzór po prostu sprowadza problem znajdowania sinusa do problemu dodawań, mnożeń i dzieleń, a te już potrafi wykonać. Wyprzedzając pytanie a jak potrafi dodawać. Kręci mnie, żeby wejść w temat techniki cyfrowej i to wytłumaczyć, ale na to bym musiał poświęcić osobny blog. 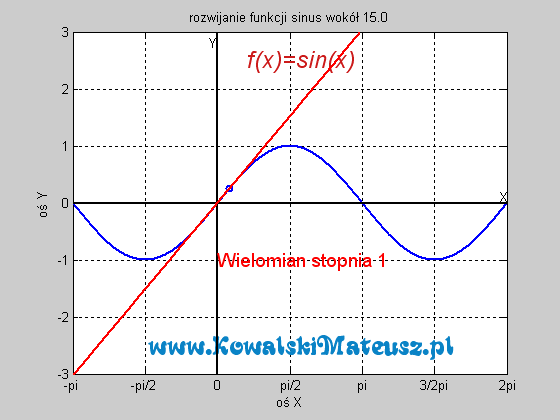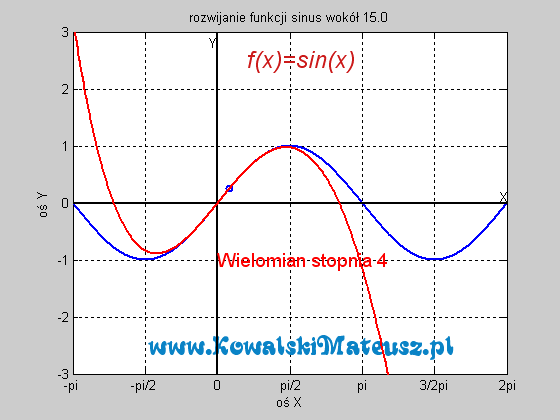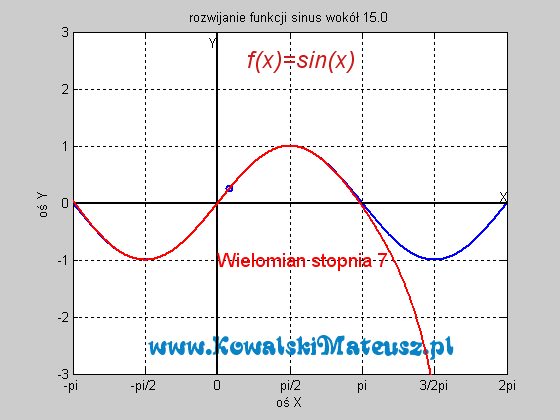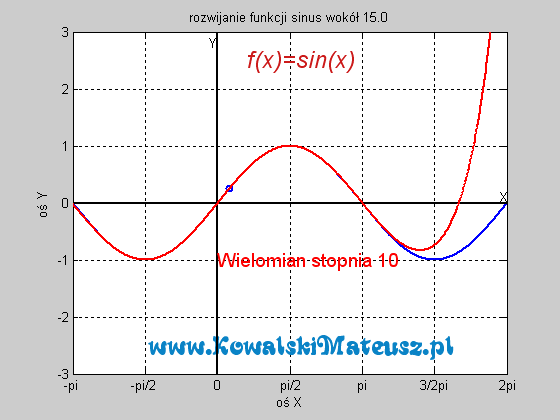

![]()
![]() to argument wokół, którego rozwijamy
to argument wokół, którego rozwijamy![]() to n-ta pochodna funkcji, która aproksymujemy
to n-ta pochodna funkcji, która aproksymujemy![]() to reszta Lagrange’a, o której kiedyś napiszę. Może nie jest to zbyt eleganckie, ale dla jasności możesz na początek przyjąć, że jest to 0.
to reszta Lagrange’a, o której kiedyś napiszę. Może nie jest to zbyt eleganckie, ale dla jasności możesz na początek przyjąć, że jest to 0.![]()
![]()
![]() to wówczas szereg Taylora nazywany jest szeregiem Maclaurina dla funkcji sinus ma postać
to wówczas szereg Taylora nazywany jest szeregiem Maclaurina dla funkcji sinus ma postać ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

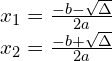
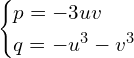
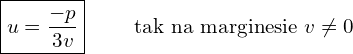
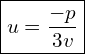
![Rendered by QuickLaTeX.com \frac{1}{v_1} = \sqrt[3]{\frac{-2}{q\R{\mp} \sqrt{\Delta}}}=\sqrt[3]{\frac{-2(q\pm \sqrt{\Delta})}{q^2-\Delta}}= \sqrt[3]{\frac{q\pm \sqrt{\Delta}}{2 \frac{p^3}{3^3}}}=\frac{3}{p}\sqrt[3]{\frac{-q\R{\mp} \sqrt{\Delta}}{2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a9fb080d45947c9a90eada60d0e53698_l3.png)
![Rendered by QuickLaTeX.com \boxed{ y_0 = 2\sqrt[3]{-\frac{q}{2}}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3dc08c0b58315bcd86559c26ade95af1_l3.png)
![Rendered by QuickLaTeX.com \boxed{y_1=y_2 = -\sqrt[3]{-\frac{q}{2}}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-dfe70a705a2a572fb3c914027b86f7b8_l3.png)