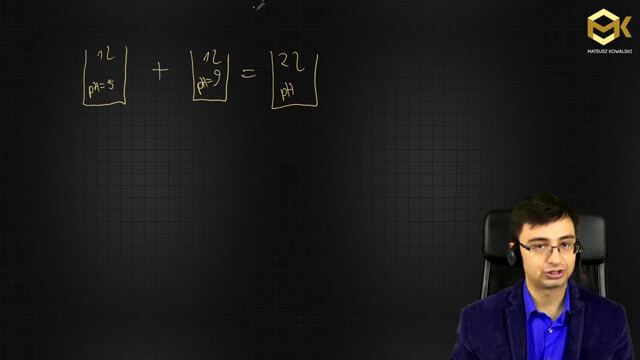Zawartość początkowej postaci pliku z filmu.

Month: luty 2016
Od Jednomianu Do Wielomianu
Zadanie Na Pomyślenie Na Poziomie Szkoły Średniej
Jakie pH ma woda zmieszana z wód o pH=5 i pH=9
Macierz Obrotu Wokół Dowolnej Osi o Dowolny Kąt w Przestrzeni 3D
Dany jest punkt ![]() o współrzędnych
o współrzędnych ![]() . Wykonujemy obrót tego punktu wokół dowolnej osi zorientowanej tak jak wektor
. Wykonujemy obrót tego punktu wokół dowolnej osi zorientowanej tak jak wektor ![]() . Wektor ten jest wektorem jednostkowym, tzn
. Wektor ten jest wektorem jednostkowym, tzn ![]() . Oś obrotu przechodzi przez początek układu współrzędnych. Obrót wykonamy o kąt skierowany
. Oś obrotu przechodzi przez początek układu współrzędnych. Obrót wykonamy o kąt skierowany ![]() . Aby dokonać takiego obrotu trzeba wykonać następujące mnożenie.
. Aby dokonać takiego obrotu trzeba wykonać następujące mnożenie.
![]()
gdzie punkt ![]() zapiszemy na potrzeby rachunku macierzowego w postaci takiej
zapiszemy na potrzeby rachunku macierzowego w postaci takiej  , wektor
, wektor ![]() zapiszemy podobnie jako
zapiszemy podobnie jako 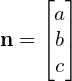 . Natomiast macierz
. Natomiast macierz ![]() ma następującą postać.
ma następującą postać.
![Rendered by QuickLaTeX.com \[\mathbf{M} = \begin{bmatrix} a^2(1-\cos \varphi) + \cos \varphi & ab(1-\cos \varphi) - c\sin \varphi & ac(1-\cos \varphi) + b\sin \varphi \\ ab(1-\cos \varphi) + c\sin \varphi & b^2(1-\cos \varphi) + \cos \varphi & bc(1-\cos \varphi) - a\sin \varphi \\ ac(1-\cos \varphi) - b\sin \varphi & bc(1-\cos \varphi) + a\sin \varphi & c^2(1-\cos \varphi) + \cos \varphi\end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9e0c48f6f2a18dfc61171be3d0dea086_l3.png)
Można to także zapisać skrótowo.
![Rendered by QuickLaTeX.com \[\mathbf{M} = \mathbf{n} \mathbf{n}^T(1-\cos \varphi) + \mathbf{I}\cos \varphi +\begin{bmatrix} 0 & -c & b \\ c & 0 & -a \\ -b & a & 0 \end{bmatrix}\sin \varphi\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-27ed306da5eca1c0814187193a53ae89_l3.png)
Obejrzyj w wersji wideo poniżej.
Continue reading