Najpopularniejsza jest średnia arytmetyczna stosowałeś ją nie jednokrotnie. Przy liczeniu średniej ocen w szkole. Czyli dodawałeś wszystkie oceny, a następnie otrzymany wynik dzieliłeś przez ilość tych ocen.
Zwrócę Twoją uwagę na fakt, że nie zawsze jest to średnia odpowiednia do danego problemu.
Poniżej prezentuje interpretacje geometryczną średnich, ale tylko dla dwóch liczby. Zakładając, że te liczby to długość podstaw trapezów.
Długość niebieskiego odcinka jest właśnie średnią arytmetyczną czyli 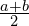

Długość odcinek czerwonego to średnia kwadratowa 
Długość odcinka zielonego to średnia geometryczna 
Długość odcinka brązowego to średnia harmoniczna 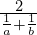
Powyższy trapezu pięknie obrazuje słuszność nierówności Cauch’ego o średnich, która głosi, iż średnia kwadratowa jest zawsze większa bądź równa od średniej arytmetycznej, ponadto iż średnia arytmetyczna jest zawsze większa bądź równa od średniej geometrycznej oraz, że średnia geometryczna jest zawsze większa bądź równa średniej harmonicznej dla tego samego zestawu danych.
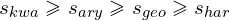
No dobrze, ale Ty pewnie zapytasz, a do czego są potrzebne te inne średnie.
To jedźmy po kolei.
Średnia harmoniczna
Przykład 1.
Używana jest przy obliczaniu średniej prędkości pojazdu powiedzmy że pojazd z Warszawy do Krakowa jechał ze średnią prędkością 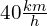 a następnie z Krakowa do warszawy ze średnią prędkością
a następnie z Krakowa do warszawy ze średnią prędkością  . Jego średnia prędkość wynosi
. Jego średnia prędkość wynosi 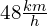 . Dlaczego? A no dlatego, że może i drogi są tej samej długości, ale czas jazdy z mniejszą prędkością jest większy, niż czas jazdy z większą prędkością a prędkość to droga podzielony przez czas.
. Dlaczego? A no dlatego, że może i drogi są tej samej długości, ale czas jazdy z mniejszą prędkością jest większy, niż czas jazdy z większą prędkością a prędkość to droga podzielony przez czas.
Przykład 2.
Jak byś połączył dwa rezystory równolegle jeden o oporze  i drugi o oporze
i drugi o oporze 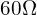 to możesz je zastąpić dwa rezystorami o oporze
to możesz je zastąpić dwa rezystorami o oporze  (średnia harmoniczna) połączonych także równolegle.
(średnia harmoniczna) połączonych także równolegle.
Przykład 3.
Jeżeli jedna pompa jest w stanie napełnić cały basen w 4 godzin, a druga pompa jest w stanie napełnić cały basen w 6 godzin. To w jakim czasie te dwie pompy pracując razem sa w stanie napełnić basen? -> odpowiedź w czasie 2,4 godziny czyli połowy średniej harmonicznej, czyli analogicznie jak w rezystorach.
Średnia geometryczna
Przykład 1.
Poziom zysku w pewnej firmie w kolejny 3 miesiącach wynosił odpowiednio 500zł, 750zł i 825zł. Jaki jest średni względny przyrost zysku.
 <- przyrost między 1 a 2 miesiącem
<- przyrost między 1 a 2 miesiącem
 <- przyrost miedzy 2 a 3 miesiącem
<- przyrost miedzy 2 a 3 miesiącem
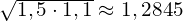 <- średni przyrost
to oznacza, że gdy na początku zysk wynosił 500zł i gdyby przyrost zysku był cały czas taki sam i wynosił 1.2845 to w trzecim miesiącu uzyskalibyśmy także 825zł zysku.
Przykład 2.
<- średni przyrost
to oznacza, że gdy na początku zysk wynosił 500zł i gdyby przyrost zysku był cały czas taki sam i wynosił 1.2845 to w trzecim miesiącu uzyskalibyśmy także 825zł zysku.
Przykład 2.
Pewien bank oferuje 3 letnią lokatę o oprocentowaniu zmiennym 6%, 7% i 8% w kolejnych latach albo o stałym oprocentowaniu 7,2%, która opcja jest korzystniejsza ?
W pierwszym wariancie mamy 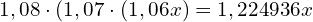 ,
,
gdzie to kwota początkowa.
to kwota początkowa.
Natomiast w wariancie 2 mamy 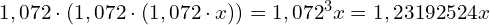
Czyli minimalnie wariant 2 jest lepszy.
Średnia arytmetyczna
Przykład 1.
do obliczania średniej ocen
przykład: Uczeń ma następujące oceny(, z których każda ma taką samą wagę): 3 4 5 4 3 4
średnia wynosi 
Przykład 2.
Dwóch lekarzy bada pacjentów. czas wizyt poszczególnych pacjentów u pierwszego lekarza wynosiły 10, 15, 20, 5, 10, 5, 10, 15, 15
u drugiego lekarza wynosiły: 10, 15, 5, 10, 10, 8, 12, 10 , 20
średnia pierwszego to 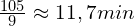
średnia drugiego to 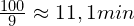
Średnia kwadratowa
Przykład 1.
Stefan ma 3 działki ziemi o kwadratach o boku 10m, 20m, 30m, chce podzielić ziemię po równo między swoimi dziećmi Zosią, Marysią i Tomkiem. Postanowił zamienić działki na 3 także kwadratowe lecz jednakowej wielkości jaki musi być bok takich działek.
Stosując wzór średniej kwadratowej mamy 
uzyskujemy, że działki powinny być o boku 21,60m
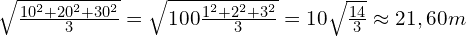
![]()