Plik ze skryptem do obliczeń w Octave’ie znajduje się
pod tym linkiem obliczenia.
Month: sierpień 2016
Matematyka, Wzór Taylora i Maclaurina, Przybliżanie Funkcji
Czy zastanawiałeś się kiedyś jak komputer lub kalkulator oblicza np.
![]()
![]()
![]()
![]()
Takie obliczenia wykonuje na co dzień twój komputer w grach, podczas obracania grafiki, czy ogólnie w przestrzeniach 3D. Podobnie smartfon np. przelicza sygnały z czujników przyspieszenia.
Jest Twierdzenie w matematyce, które pozwala na zamianę tych niewdzięcznych funkcji na szereg dodawań, odejmowań, mnożeń i dzieleń.
Oczywiście nie jesteśmy w stanie idealnie zastąpić tych funkcji tylko tymi 4 działaniami.
Nie mniej jednak możemy to zrobić dowolnie dokładnie.
A wręcz możemy z góry zapewnić, że wynik nie będzie różnił się bardziej, niż o np.
![]()
![]()
![]()
Polega to na tym, iż funkcję zastępujemy wielomianem. Ponieważ obliczenie wartości wielomianu dla danej liczby sprowadza się do mnożenia i dodawania.
To natomiast potrafimy zrobić nawet ręcznie dla dowolnej liczby, również z przecinkiem.
Przykładowo dla wielomianu
![]()
chcemy obliczyć wartość dla ![]()
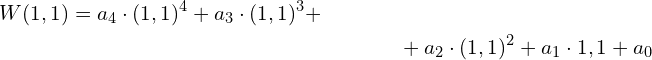
Wprawdzie jest tam także potęgowanie, ale to inaczej mnożenie, bo jest to potęga naturalna.
![]()
Pierwszy rzut oka.
![]()
![]()
![]()
Były to funkcje rozwijane w punkcie dla argumentu ![]() .
.
Okazuje się, że funkcje mogą być rozwijane w innym punkcie.
![]() rozwijając w punkcie dla argumentu
rozwijając w punkcie dla argumentu ![]()
![]() rozwijając w punkcie dla argumentu
rozwijając w punkcie dla argumentu ![]()
![]() rozwijając w punkcie dla argumentu
rozwijając w punkcie dla argumentu ![]()
Możemy rozwijać w każdym punkcie, choć nie wszystkie są odpowiednie, ale o tym dalej.
Jak to w matematyce, każde twierdzenie potrzebuje jakiegoś założenia.
Co jest zatem wymagane i jakie są ograniczenia?
Funkcja musi być przynajmniej ![]() razy różniczkowalna na pewnym przedziale.
razy różniczkowalna na pewnym przedziale.
Co dla większości typowych funkcji jest od razu spełnione.
Gdyż większość znanych nam funkcji
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Są różniczkowalne dowolną liczbę razy i to na całym przedziale dziedziny. No z wyjątkiem brzegów dziedziny, gdzie wystarczy nam różniczkowalność jednostronna.
Weźmy przykład do obliczenia ![]() .
.
Szukamy argumentu, dla którego znamy wartość tej funkcji ![]() i wartości jej kolejnych pochodnych.
i wartości jej kolejnych pochodnych.
Wiemy, że pochodną funkcji ![]() jest
jest ![]() a kolejną pochodną znowu
a kolejną pochodną znowu ![]() itd.
itd.
Argument natomiast możemy wybrać np. 0 lub 1, a nawet inne. Generalnie im bliżej tych 1,21 to tym lepiej.
Czasem warto wziąć trochę dalszy argument, a mieć łatwiejsze potem liczby do podstawienia, choć może być to okupione potrzebą większej liczby składników, ale o tym za chwilę.
Wybierę zatem 0 , gdyż ![]() co jest dosyć wygodne.
co jest dosyć wygodne.
Twierdzenie głosi, że możmemy funkcję ![]() zapisać tak
zapisać tak
![]()
Ta liczba z wykrzyknikiem to skrótowy zapis mnożeń kolejnych liczb naturalnych np.
![]()
![]()
Nazywa się to silnią.
![]()
Im więcej tych składników wypiszemy tym mamy dokładniej.
![Rendered by QuickLaTeX.com \[e^x= \underbrace{e^0}_{\mbox{{\tiny pierwszy}}}+ \underbrace{\frac{e^0}{1!}x}_{\mbox{{\tiny drugi}}}+ \underbrace{\frac{e^0}{2!}x^2}_{\mbox{{\tiny trzeci}}}+ \underbrace{\frac{e^0}{3!}x^3}_{\mbox{{\tiny czwarty}}}+ \frac{e^0}{4!}x^4+\ldots\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-f6dd1806d7930682b018cf0d5f27612d_l3.png)
Weźmy do naszego przykładu 4 pierwsze składniki rozwinięcia
![]()
Mamy zatem
![]()
to potrafimy nawet ręcznie, pisemnie policzyć.
Pojawia się tylko pytanie na ile dokładne jest to nasze przybliżenie?
Okazuje się, iż cały błąd, który powstał z wypisania nie wszystkich składników rozwinięcia można wyrazić tak.
![]()
gdzie ![]() jest liczbą pomiędzy
jest liczbą pomiędzy ![]() a
a ![]() .
.
Przypomina to wypisanie kolejnego składnika sumy lecz zamiast ![]() jest
jest ![]() .
.
![]()
Po dodaniu mamy równość
![]()
gdzie ![]()
Trzeba przyznać, iż jest to bardzo ciekawe.
Mimo nieznajomości dokładnej wartości ![]() wiemy, że tym dodatkowym składnikiem, zwanym resztą we wzorze Taylora, możemy IDEALNIE “załatać”, tę niedokładność spowodowaną zakończonym wypisywaniem składników.
wiemy, że tym dodatkowym składnikiem, zwanym resztą we wzorze Taylora, możemy IDEALNIE “załatać”, tę niedokładność spowodowaną zakończonym wypisywaniem składników.
Wprawdzie niewiadomo ile wynosi ![]() , ale wiadomo, że istnieje taka liczba
, ale wiadomo, że istnieje taka liczba ![]() z zakresu
z zakresu ![]() i
i ![]() , że wstawiona do tej reszty skompensuje idealnie błąd, gdy tę resztę dodamy do rozwinięcia. tzn.
, że wstawiona do tej reszty skompensuje idealnie błąd, gdy tę resztę dodamy do rozwinięcia. tzn.
![]()
Skoro wiemy w jakim przedziale znajdzie się ![]() to możemy oszacować przy jakiej
to możemy oszacować przy jakiej ![]() ta reszta będzie największa. Co za tym idzie będziemy mieć pewność, że nasz błąd przybliżenia nie jest większy, niż ta reszta.
ta reszta będzie największa. Co za tym idzie będziemy mieć pewność, że nasz błąd przybliżenia nie jest większy, niż ta reszta.
Dla ![]() równego
równego ![]() reszta może być największa
reszta może być największa
![]()
![]()
![]()
tak więc nasz wynik nie różni się bardziej od tego prawdziwego, nieznanego, niż o ![]() .
.
Nasze przybliżenie możemy poprawić wypisując więcej składników.
Dopiszmy kolejny składnik wynik będzie wynosił.

z błędem nie większym, niż
![]()
Zobaczmy co Się stanie jak rozwiniemy naszą funkcję ![]() bliżej szukanego argumentu tzn. dla
bliżej szukanego argumentu tzn. dla ![]() .
.
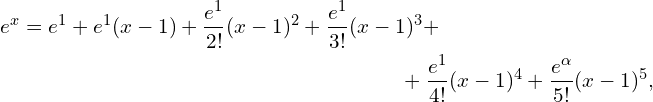
gdzie ![]() jest pomiędzy
jest pomiędzy ![]() a
a ![]() .
.
W tym wypadku otrzymamy

Z błędem nie większym niż,
![]()
Z tym, że teraz musimy stosować dokładne przybliżenie liczby ![]() i na nim operować.
i na nim operować.
Kolejny przykład powiedzmy, że chcemy obliczyć ![]() .
.
Szukamy argumentu, dla którego znamy wartość tej funkcji i jej kolejnych pochodnych.
Wiemy, że pochodną sinus jest kosinus, kolejną pochodną sinus, kolejną kosinus itd. (no i jeszcze okresowa zmiana znaku)
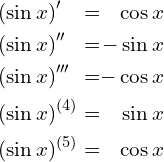
Natomiast argument może być np. ![]() lub
lub ![]() ,
, ![]() lub
lub ![]() a nawet inne. Podobnie jak wcześniej im bliżej tych
a nawet inne. Podobnie jak wcześniej im bliżej tych ![]() tym dokładniej.
tym dokładniej.
Wybieram zatem ![]() , gdyż
, gdyż ![]() i
i ![]() .
.
Twierdzenie mówi, że możemy zapisać
![]()
Weźmy 4 pierwsze składniki tej sumy (odejmowanie to też dodawanie elementu przeciwnego).
Mamy zatem:
![]()
Zamieńmy stopnie na liczby, aby wyglądało to bardziej normalnie, zgodnie z przelicznikiem znanym z trygonometrii.
![]()
![]()
z resztą ![]()
oraz błędem nie większym, niż
![]()
Skąd wiedzieć ile wyrazów należy wypisać, aby uzyskać zadana dokładność.
Powiedzmy, że chcemy obliczyć ![]() z dokładnością przynajmniej
z dokładnością przynajmniej ![]()
Musimy jeszcze zdecydować się, gdzie będziemy rozwijać, gdyż od tego zależy ile tych wyrazów będzie.
Znamy pierwiastek dla ![]() i
i ![]() . Decydujemy się na rozwijanie wokół
. Decydujemy się na rozwijanie wokół ![]()
Teraz możemy oszacować ile wyrazów trzeba wypisać aby osiągnąć zadaną dokładność.
Reszta ma postać
![Rendered by QuickLaTeX.com \[R_n(x,x_0)=\frac{\left(\sqrt{\alpha}\right)^{(n+1)}}{(n+1)!}(x-x_0)^{n+1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-e9d50861ca14aae9fc3f8ba34bd3b20f_l3.png)
Tutaj wyszła nam jeszcze jedna ważna kwestia, iż wypadałoby znać wzór na ![]() -tą pochodną funkcji
-tą pochodną funkcji ![]()
![]()
Choć nie jest to konieczne, to zaobserwujmy prawidłowość \newline

Sprawdźmy czy ![]() pierwsze wyrazy wystarczą
pierwsze wyrazy wystarczą ![]()
wówczas reszta to
![Rendered by QuickLaTeX.com \[\left|\frac{\frac{3}{8}\cdot \frac{1}{13,71^2\sqrt{13,71}}}{3!}(13,71-16)\right| <\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-02fd43810c0d12996a862bbee1670345_l3.png)
![Rendered by QuickLaTeX.com \[<\left|\frac{\frac{3}{8}\cdot \frac{1}{13^2\sqrt{13}}}{3!}(13-16)\right| < 0,000308\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b1a7d4b7cc63bfc20cabbaf58c8689da_l3.png)
czyli za mała dokładność.
Sprawdźmy czy ![]() składniki wystarczą
składniki wystarczą ![]()

To już zapewni nam dokładność lepszą niż ![]() .
.
Tak więc przybliżona wartość ![]() obliczmy w ten sposób:
obliczmy w ten sposób:

Warto zdawać sobie sprawę, że jeśli okazało by się, że wyrazów potrzeba dużo, to wtedy trzeba znać wzory wszystkich kolejnych pochodnych.
W przypadku obliczeń ręcznych nie jest to aż tak straszne, lecz w przypadku implementacji tego na komputerze trzeba znać ogólny wzór na ![]() -tą pochodną od razu.
-tą pochodną od razu.
Ponieważ komputer tego sam nie wyprowadzi, tzn. jest to możliwe, ale to rozważania na zupełnie innym poziomie i faktycznie komputery potrafią takie rzeczy robić.
No chyba, że mamy jakiś szczególny przypadek, gdzie z góry znana jest ich wartość po podstawnieniu argumentu wokół, którego rozwijamy.
Teraz formalnie. Funkcję ![]() można rozwinąć w szereg Taylora w punkcie
można rozwinąć w szereg Taylora w punkcie ![]() zgodnie ze wzorem.
zgodnie ze wzorem.
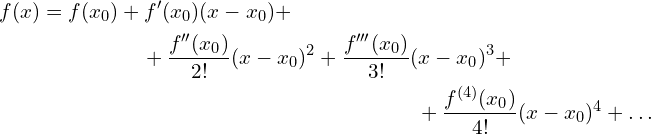
Oczywiśćie w każdym miejscu możemy zakończyć i dodając resztę we wzorze Taylora.
Jeśli funkcja jest tylko ![]() razy różniczkowalna to wówczas w taki sposób
razy różniczkowalna to wówczas w taki sposób
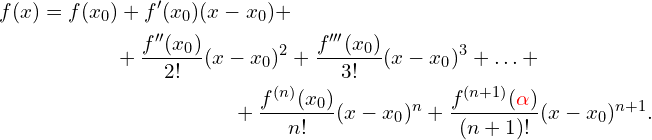
Ostatnie różniczkowanie, lub wcześniej, zostawiamy sobie na resztę
(Lagrange’a)
Tą resztę we wzorze Taylora, można mieć wiele postaci, ale to nie jest najważniejsze, tę którą używaliśmy do tej pory nazywamy resztą Lagrange’a.
Zapytasz Mateusz, ale po co się tym zajmować? To już od dawna jest wdrożone na bardzo niskim poziomie?
Aby wiedzieć. Nie czułeś/ czułaś nigdy satysfakcji, że coś wiesz?
W kwestii nazewnictwa:
Twierdzenie Taylora mówi o możliwości takiego przedstawienia.
Wzór Taylora to przedstawienie za pomocą wielomianu czyli skończona liczba składników ![]() reszta.
reszta.
Jeśli funkcja jest dowolnie razy różniczkowalna to takie przedstawienie nazywamy szeregiem Taylora, bo rozwijanie ciągnie się bez końca.
Rozwijanie w punkcie dla argumentu ![]() nazywamy rozwijanie w szereg Maclaurina.
nazywamy rozwijanie w szereg Maclaurina.
Istnieje odpowiednik tego twierdzenia na funkcje dwóch zmiennych, a nawet dowolnej liczby zmiennych, nawet poza zbiorem liczb rzeczywistych, a nawet w jeszcze bardziej abstrakcyjnej wersji, co też poświadcza o sile tego twierdzenia.
Funkcja ![]() jest przykładem, że rozwijanie w złym miejscu może być bardzo wolno zbieżne.
jest przykładem, że rozwijanie w złym miejscu może być bardzo wolno zbieżne.
Gdyż mimo 50 stopnia wielomianu to ta aproksymacja nie porusza się za bardzo dalej.
Warto zapamiętać, iż funkcję bardziej poziome nie są najlepsze do rozwijania w szereg Taylor’a.
Tak na marginesie nigdzie nie znalazłem wzoru na ![]() -tą pochodną funkcji
-tą pochodną funkcji ![]() .
.
Ponadto wzór na ![]() -tą pochodną
-tą pochodną ![]() jest bardzo skomplikowany.
jest bardzo skomplikowany.
Jak komputer oblicza ![]() ?
?
Na ![]() stosuje się szereg, który rozwija wokół
stosuje się szereg, który rozwija wokół ![]() i otrzymuje się w inny sprytny sposób, ale to już oddzielna historia.
i otrzymuje się w inny sprytny sposób, ale to już oddzielna historia.




