Algorytm CORDIC – Odcinek 2 | Kowalski Mateusz.pl

Poprzedni odcinek znajduje się pod adresem https://www.kowalskimateusz.pl/algorytm-cordic-odcinek-1/

Polecam wersje pdf tego artykułu jest lepiej sformatowana.

Algorytm CORDIC odcinek 2 Pobierz wersje pdf

Następny odcinek znajduje się pod adresem https://www.kowalskimateusz.pl/algorytm-cordic-odcinek-3/

Uogólniony Algorytm CORDIC

Algorytm CORDIC możemy uogólnić dokładając parametr $\mu$ . Parametr $\mu$ może przyjąć
wartość $\mu \in \nawiasw{-1, 0, 1}$ . Oczywiście gdy $\mu = 1$ uzyskujemy tryb rotacyjny
i wektorowy wspólnie nazwany (Circular). Po polsku to będzie coś w stylu okrągły, kolisty,
okrężny, okręgowy. Dla $\mu = 0$ otrzymujemy tryb liniowy. Ten tryb pozwala na obliczanie
mnożenia i dzielenia bez wykonywania mnożenia i dzielenia wprost. Gdy $\mu = -1$ otrzymujemy
tryb hiperboliczny. Jednak w trybie hiperbolicznym jest kilka uwag co do tego wzoru.

Wyróżnić możemy zatem 6 trybów. Aby określić, o którym trybie mówimy trzeba podać dwa określenia.
Pierwsze określenie aby wskazać jakie $\mu$ mamy na myśli. Drugie czy chodzi o tryb rotacyjny
czy tryb wektorowy.

W literaturze zwykle zamiast $\beta$ używane jest oznaczenie $z$ , ale ja zostanę przy $\beta$ ,
bo $z$ kojarzy się z osią $z$ , tym bardziej, że zmienne $x$ i $y$ oznaczają właśnie
współrzędne w układzie współrzędnych.
Należy zdawać sobie sprawę, że $\beta$ oznacza kąt tylko w trybie okrężnym.

Pewien przesuw pionowy

Rozważmy punkt $A = \nawias{A_x, A_y}$ oraz wektor pionowy $\varphi$ , tzn. równoległy do
osi $y$ . Niech ten wektor będzie umieszczony na prostej o równania $x = 1$ i niech określa
przesunięcie punkt $A$ w sposób przedstawiony na rysunku. W wyniku tego przesunięcia
punktu $A$ otrzymujemy obraz, czyli punkt $A' = \nawias{A'_x, A'_y}$ .
Współrzędna $x$ jest taka sama $A'_x = A_x$ , natomiast $A'_y = A_y + A_x\varphi$ . Zależność ta wynika
z trójkątów podobnych. Oczywiście tak zdefiniowany przesuw jest addytywny, tzn.
skutek wykonania kolejnych dwóch jest taki sam jak jednego będącego ich sumą.

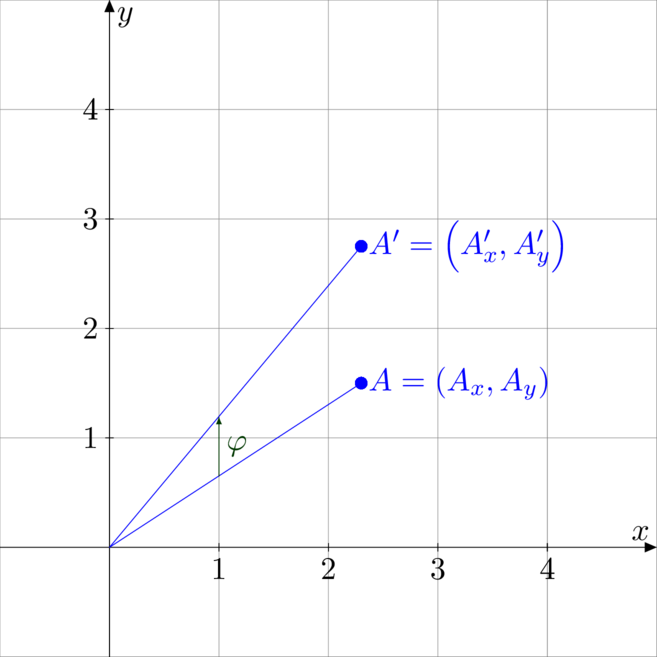
Rozkład liczby na sumę ułamków

Rozważmy ciąg geometryczny, w przypadku skończonym lub szereg geometryczny, w przypadku
nieskończonym o ilorazie $q = \frac{1}{2}$ , czyli
$1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \ldots$ .
Ten ciąg oznaczamy przez $\nawias{\gamma_k}$ o wyrazie ogólnym $\gamma_k = 2^{-k}$ .
W tym przypadku, $\gamma_k$ nie oznacza kąta.

Następnie na bazie tego ciągu rozważmy nowy ciąg $\nawias{\varphi_k}$ , którego wyrazy
$\varphi_k$ są wyrazami tego ciągu z tym, że niektórym zmieniono znak na przeciwny.

Okazuje się wówczas, że każdą liczbę z przedziału od
$-2$ do $2$ jesteśmy w stanie uzyskać jako sumę skończoną
$b = \varphi_0 + \varphi_1 + \ldots + \varphi_{n-1}$ lub jako granicę takiego ciągu
$b = \varphi_0 + \varphi_1 + \ldots$ . Pozostawiam to bez dowodu. Przykładowo

W zasadzie ten przedział jest domknięty czyli włącznie z liczbami $2$ i $-2$ , gdyż 2
otrzymamy w granicy gdybyśmy zawsze brali z plusem każdy wyraz, jest to wówczas suma
szeregu geometrycznego. Analogicznie $-2$ to także suma szeregu geometrycznego,
więc każdą liczbę $a\in \nawiask{-2, 2}$ możemy tak rozpisać.
Jednak lepiej przyjąć ten przedział bez $2$ i $-2$ , tzn. $a\in\nawias{-2,2}$ . Zauważmy, że 2
to inaczej $1\cdot 2$ , a $1$ ma skończone rozwinięcie, w zasadzie to jest nim tylko 1 wyraz.
Mnożenie przez 2 to przesuniecie bitów w lewo.

Dobór znaków

Ponownie trzeba zapytać jak dobierać znaki? Analogicznie jak w poprzednich trybach.
Zamiast sumować kolejne $\varphi_k$ do momentu, aż uzyskamy wartość $b$ .
Możemy z kroku na krok modyfikować tę wartość aż osiągnie ona 0.
Niech $\beta_k$ oznaczymy pozostałą cześć liczby $b$ do rozłożenia,
po $k$ -tej iteracji. Z kroku na krok modyfikujemy $\beta_k$ , mianowicie
$\beta_{k+1} = \beta_k - \varphi_k$ .
Jeśli bieżące $\beta_k>0$ , to następny składnik $\gamma_k$ należy odjąć.
Jak $\beta_k<0$ , to następny składnik $\gamma_k$ należy dodać.

Rzecz jasna $\beta_0 = b$ . Załóżmy, że chcemy przemnożyć daną liczbę $a$ przez
daną liczbę $b=\frac{7}{5}$ , wówczas

Mnożenie to suma liczb, które były odpowiednio poprzesuwane bitowo oraz możliwe, że
zmieniono im wartość na przeciwną. Zauważmy, że $\beta_k$ oznacza także jaka cześć
liczby $b$ pozostała jeszcze do przemnożenia z $a$ .
Niech $x_k$ oznacza wartość liczby $a$ . W każdej iteracji $x_k$ jest takie samo.
Ta zmienna w tym trybie jest w zasadzie zbędna, ale dla spójności z pozostałymi
trybami zostawmy ją. Niech zmienna $y_k$ oznacza bieżąca wartość iloczynu po $k$ -tej
iteracji.

$A'_y = A_y + A_x\varphi \quad \to \quad y_{k + 1} = y_{k} + a\varphi_k \quad \to \quad$

$\quad \to \quad y_{k + 1} = y_{k} + \sgn(\beta_k)a\cdot 2^{-k}$

Oczywiście $y_0 = 0$ . Uzyskujemy zatem układ rekurencji

$\begin{cases}x_{k + 1} = x_{k} \\y_{k + 1} = y_{k} + \sgn(\beta_k)x_k\cdot 2^{-k} \\\beta_{k + 1} = \beta_k - \sgn(\beta_k)\gamma_k \\x_0 = a \\y_0 = 0 \\\beta_0 = b \\\end{cases}$

Po $n$ iteracjach wynik mnożenia jest w przybliżeniu równy $y_n$ , a niekiedy nawet dokładnie równy

$a\cdot b \approx y_n$

Dla ujemnego $a$ wzór także da poprawne wyniki. W przypadku ujemnego $b$ także będą poprawne.

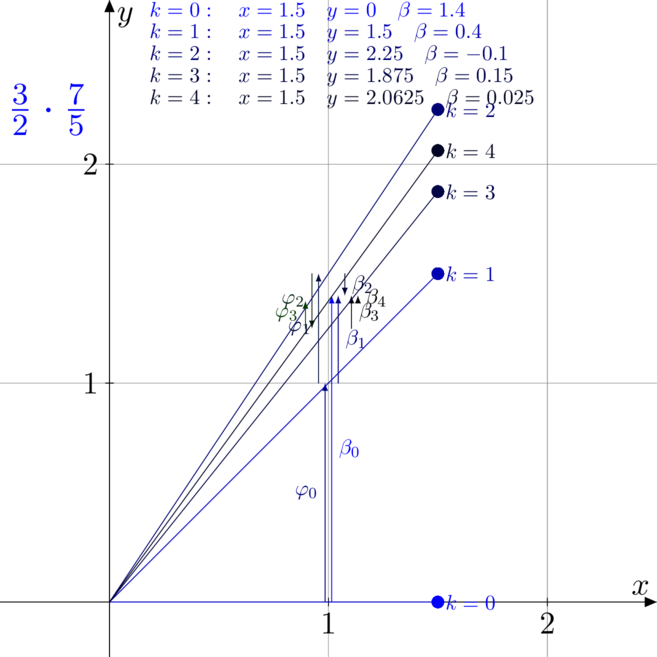
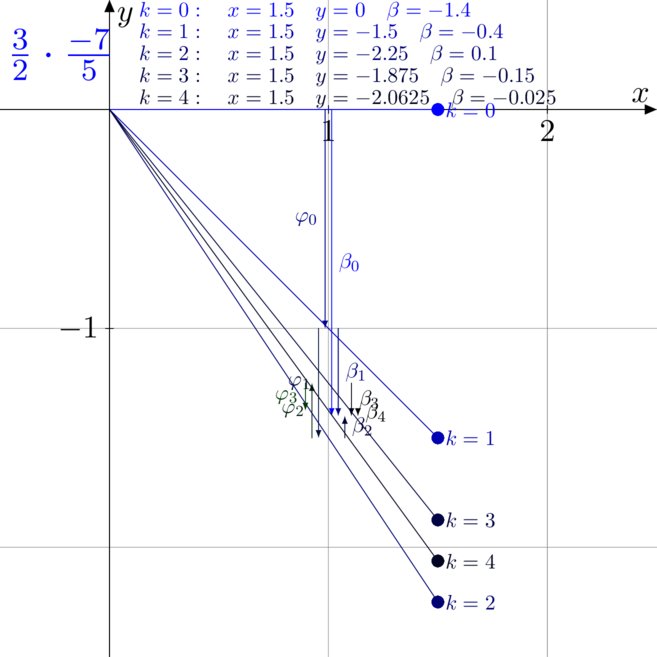
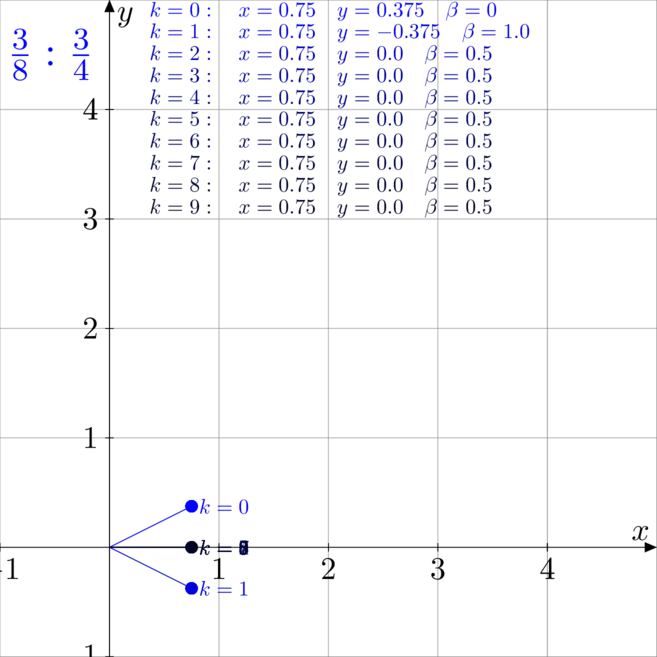
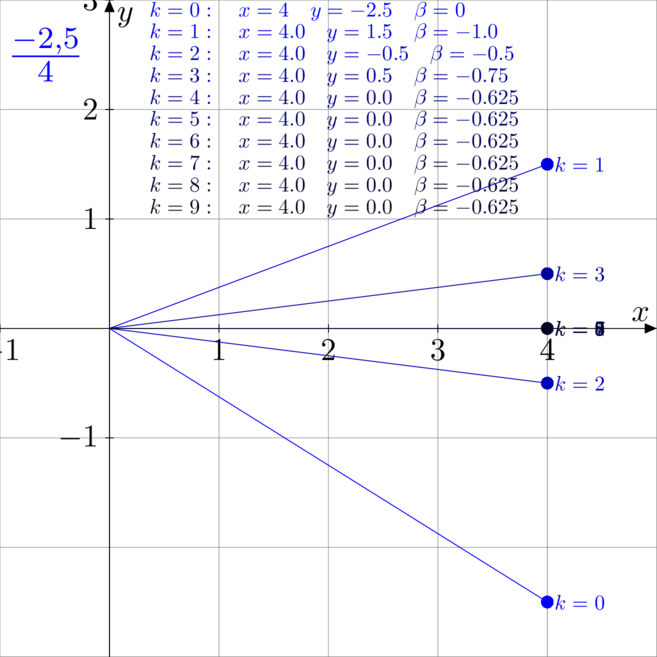
Przykłady mnożenia

Na poniższych rysunkach zwizualizowano i rozpisano kolejne kroki pracy algorytmu CORDIC
podczas mnożenia, czyli w trybie liniowym, rotacyjnym.

Rysunek pierwszy to mnożenia 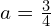$a=\frac{3}{4}$ z $b=\frac{5}{3}$ .
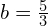Rysunek drugi to mnożenie 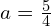$a=\frac{5}{4}$ z $b=\frac{3}{2}$ .
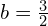Rysunek trzeci to mnożenie 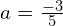$a=\frac{-3}{5}$ z $b=\frac{-2}{3}$ .
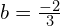Rysunek czwarty to mnożenie $a=\frac{-5}{6}$ z $b=\frac{9}{10}$ .

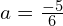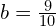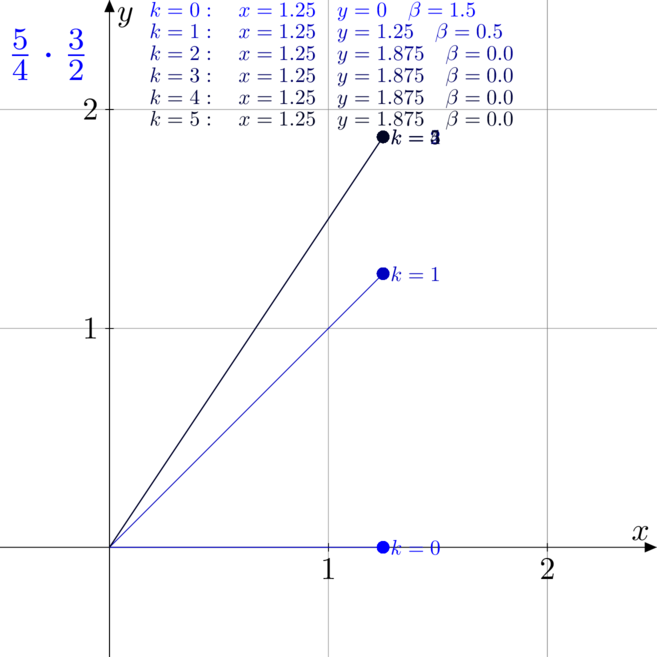
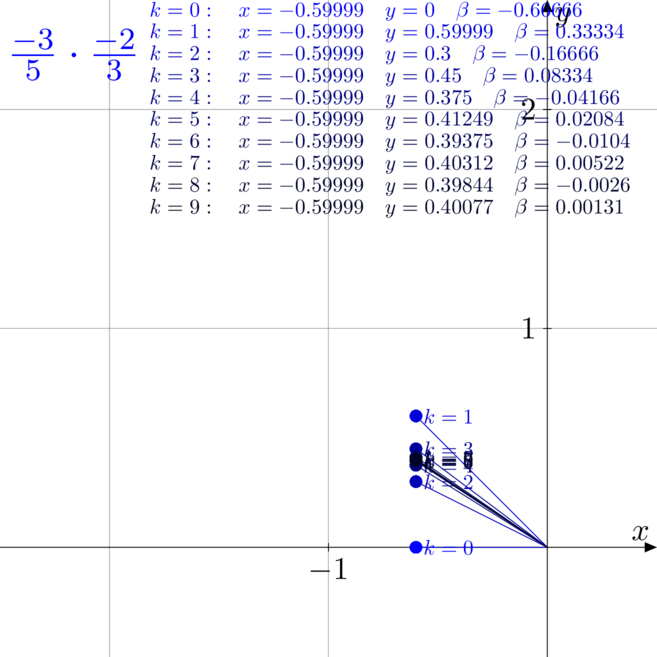
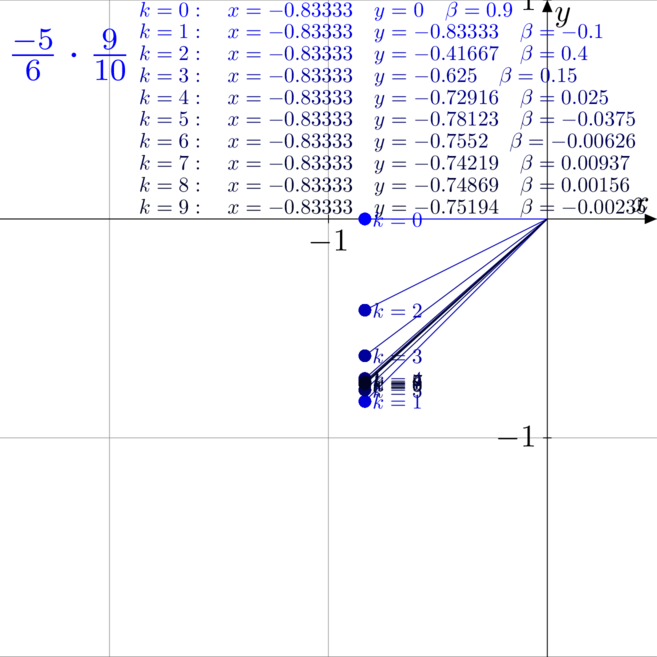
Zauważmy, że w drugim przypadku liczby wejściowe były tak dobrane, że już po drugiej iteracji
idealnie trafiliśmy w wynik, więc każda kolejna iteracja nic nie zmieniała.
Taka sytuacja zdarza się rzadko. W 4 przypadku dokładny wynik mnożenia to $\frac{-3}{4}$ ,
ale mimo to, że liczby wejściowe nie miały w mianowniku potęgi dwójki, to algorytm w małej
liczbie kroków nie trafi dokładnie w wynik.

Algorytm dzielenia

Okazuje się, że możemy także dzielić, nie wykonując dzielenia wprost.
Wyjdźmy od otrzymanego układu rekurencji, który opisuje przesuwanie się po prostej $x = a$ .
Zastanówmy się nad sposobem podzielenia liczby $c$ przez $a$ . W trybie mnożącym było tak, że liczbę $a$
mnożyliśmy przez $b$ w wyniku otrzymaliśmy $ab$ . Skutkowało to tym, że punkt $A=\nawias{a, 0}$
przesuwaliśmy pionowo, aż uzyskaliśmy punkt o współrzędnych $A'=\nawias{a, a\cdot b}$ .
Należy zatem ten proces odwrócić. Podobnie jak w trybie okrężnym, w podtrybie
rotacyjnym obracaliśmy punkt $A=\nawias{1, 0}$ , aż uzyskaliśmy obraz
$A'=\nawias{\cos\varphi, \sin\varphi}$ , w podtrybie wektorowym odwrotnie punkt
$A=\nawias{A_x, A_y}$ był obracany, aż uzyskaliśmy $A'=\nawias{A'_x, 0}$ .

Mamy zatem punkt $A=\nawias{a, c}$ , który trzeba przesunąć po linii pionowej, aż będzie
na osi $x$ , czyli $A'=\nawias{a, 0}$ . Każde kolejne przesunięcie jest o połowę mniejsze
od poprzedniego. Tak jak w trybie rotacyjnym każdy kolejny tangens kąta obrotu był
o połowę mniejszy od poprzedniego.

Można pomyśleć, że jeśli bieżący $y_k$ jest większy od 0 to należy przesunąć w dół,
czyli $\varphi_k<0$ . Jeśli bieżący $y_k$ jest ujemny to należy przesunąć w górę $\varphi_k>0$ .
Zauważmy jednak, iż $x_k$ może być ujemne, wówczas $\varphi_k$ było by źle określone.
Poprawiając będzie $\varphi_k = \epsilon_k \gamma_k = -\sgn(x_k y_k)\gamma_k$ .

Suma przesunięć $\varphi_k$ to przesunięcie punktu $A$ do punktu $A'$ . Zatem szukane przesunięcie
$A'$ do $A$ jest z przeciwnym znakiem. Ten wynik to wynik dzielenia. Niech zatem $\beta_k$
oznacza aktualnie naliczony wynik po $k$ iteracjach. Rzeczy jasna na początku wynosi 0, to
prowadzi nas do rekurencji.

$\begin{cases}\beta_{k + 1} = \beta_k - \varphi_k \\\beta_0 = 0\end{cases} \quad \to \quad \begin{cases}\beta_{k + 1} = \beta_k + \sgn(x_ky_k)\gamma_k \\\beta_0 = 0\end{cases}$

Otrzymujemy układ rekurencji

$\begin{cases}x_{k + 1} = x_{k} \\y_{k + 1} = y_{k} - \sgn(x_k y_k)x_k\cdot 2^{-k} \\\beta_{k + 1} = \beta_k + \sgn(x_k y_k)\gamma_k \\x_0 = a \\y_0 = c \\\beta_0 = 0 \\\end{cases}$

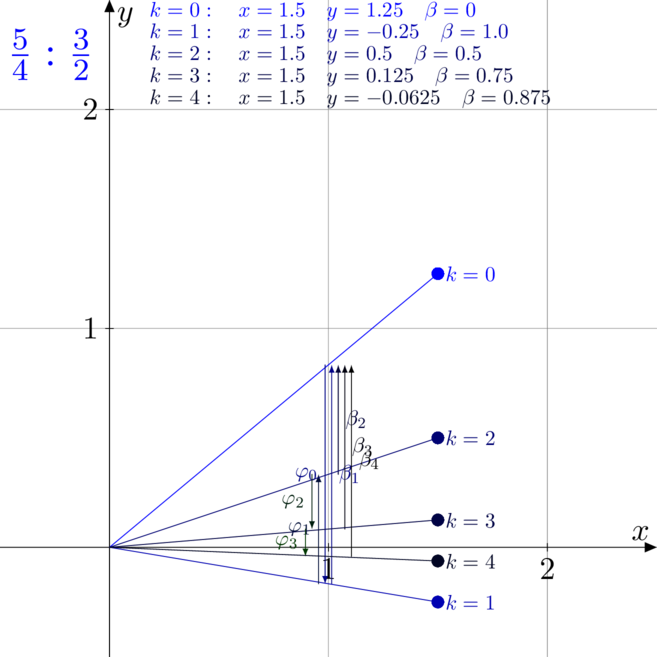
Przykłady dzielenia

Na poniższych rysunkach zwizualizowano i rozpisano kolejne kroki pracy algorytmu CORDIC
podczas dzielenia, czyli w trybie liniowym, wektorowym.

Rysunek pierwszy to dzielenie 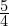$\frac{5}{4}$ przez $\frac{3}{2}$
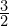
Rysunek drugi to dzielenie 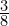$\frac{3}{8}$ przez $\frac{3}{4}$ .
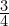Rysunek trzeci to dzielenie 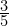$\frac{3}{5}$ przez $\frac{3}{2}$ .
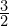Rysunek czwarty to dzielenie 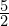$\frac{5}{2}$ przez $4$ .

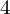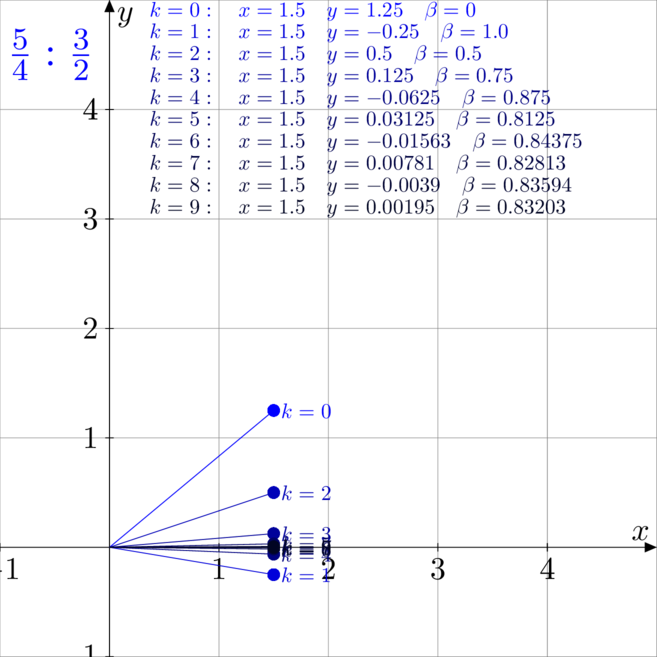
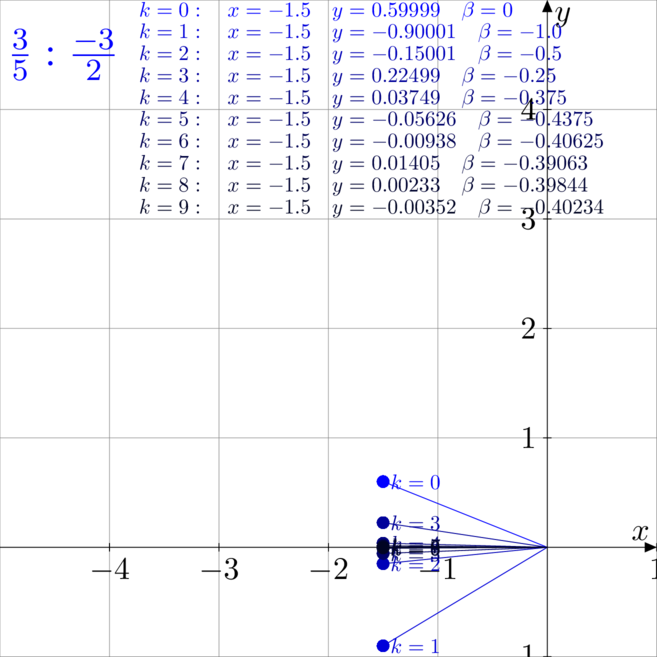
Zauważmy, iż w przypadku drugim liczby były tak dobrane, że już po drugim kroku pracy
algorytmu trafiliśmy idealnie w wynik. Kolejne iteracje nic nie zmieniały. Analogicznie
na rysunku czwartym, po czwartej nie ma zmian. Taka sytuacja zdarza się rzadko.

Co robić poza przedziałem zbieżności? – mnożenie

Algorytm CORDIC w trybie mnożenia działa poprawnie. Tylko jeśli $b\in\nawias{-2,2}$ .
Ten algorytm można łatwo zmodyfikować aby działa dla dowolnego $b$ .
W zasadzie to dla dowolnego, choć z góry ustalonego przedziału.
Należy zmodyfikować algorytm o dodatkowy parametr, nazwałem go $r\in\ZZ$ .

Jeśli chcemy zwiększyć przedział dla $b$ dwukrotnie, czyli do $b\in\nawias{-4,4}$ ,
to należy przyjąć $r = 1$ . Jeśli chcemy zwiększyć czterokrotnie to $r = 2$ .
Jeśli chcemy zwiększyć ośmiokrotnie to $r = 3$ , itd.
Jeśli nie chcemy modyfikować to $r = 0$ . Aby zachować tę samą dokładność trzeba
będzie wykonać o $r$ iteracji więcej. Czyli jeśli zwiększymy przedział 128 krotnie,
to trzeba wówczas wykonać o $r=7$ iteracji więcej, aby osiągnąć ten sam rząd
dokładności wyników co w przypadku bez rozszerzenia $r=0$ . Można to wykorzystać np.
przy liczbach stałoprzecinkowych.

Natomiast jednak jeśli dysponujemy liczbami w postaci zmiennoprzecinkowej to nie
trzeba wprowadzać tego rozszerzenia. Wówczas przedział $b\in\nawias{-2,2}$ nam wystarczy.
Liczba zmiennoprzecinkowa jest postaci $a = Z\cdot M\cdot 2^W$ . Gdzie $Z\in\nawiasw{-1,1}$
jest znakiem liczby, $M\in\left[1,2 \right)$ jest mantysą, natomiast $W\in\ZZ$
jest wykładnikiem. W praktyce jest jeszcze bias przy wykładniku, ale dla skupienia
uwagi nie komplikujmy, bo można go łatwo uwzględnić.

Mnożąc dwie liczby $a_1 = Z_1\cdot M_1\cdot 2^{W_1}$ , $a_2 = Z_2\cdot M_2\cdot 2^{W_2}$
zmiennoprzecinkowe mamy $a_1\cdot a_2 = Z_1\cdot Z_2\cdot M_1\cdot M_2\cdot 2^{W_1 + W_2}$ .
Widzimy zatem, że mnożenie liczb zmiennoprzecinkowych sprowadza się do mnożenia ich
mantys, gdzie każda z nich jest liczbą z przedziału $\left[1, 2\right)$ oraz dodawania
wykładników. Wynik iloczynu znajduje się w przedziale $\left[ 1, 4\right)$ . Możliwe,
że wymagana będzie normalizacja. Przykładowo $3,9 = 1,8\cdot 2^1$ . Wówczas do sumy
wykładnika trzeba dodać jeszcze to 1. Do algorytmu nie musimy wprowadzać żadnych modyfikacji.
Nawet możemy do algorytmu podawać te mantysy ze znakiem, gdyż
$Z\cdot M \in \left(-2, -1 \right] \cup \left[1, 2\right)$ .

Pojawia się pytanie co w przypadku zera? Zero ma ściśle określona sekwencja
bitów. Ponadto wynik mnożenia przez 0 z góry jest znany. Można zatem wykryć czy któraś
z liczb nie jest 0 i wówczas dać od razu wynik bez używania algorytmu.

Co robić poza przedziałem zbieżności? – dzielenie

W przypadku dzielenia sytuacja jest podobna do mnożenia. Mamy analogiczne dwie opcje.
Jedna to rozszerzania zbioru do takiego jakich używamy liczb. Drugie to wykorzystanie
własności liczb zmiennoprzecinkowych. Są jednak pewne różnice.

Algorytm w trybie dzielenia działa poprawnie jeśli wynik jest w przedziale $\nawias{-2, 2}$ .
Można rozszerzyć ten przedział stosując analogiczną modyfikację jak ta omówiona w trybie
mnożenia, mianowicie. Dokładając analogiczny parametr $r$ . Podobnie jak przedział
chcemy przykładowo zwiększyć 32 razy, tzn. do $\nawias{-64, 64}$ , to przyjmujemy $r=5$
i aby zachować ten sam rząd precyzji należy wykonać $r$ dodatkowych iteracji.

W przypadku liczb zmiennoprzecinkowych nie trzeba modyfikować algorytmu. Wówczas warto
wykorzystać własności liczb zmiennoprzecinkowych. Należy rozpoznać czy
przypadkiem nie chcemy wykonać dzielenia przez zero. W tym celu sprawdzić należy czy
$a\neq 0$ . Ponadto jeśli $c=0$ , to bez wykonywania dzielenia od razu wiadomo jaki jest wynik.
W pozostałych przypadkach liczbę możemy przedstawić w postaci $a = Z\cdot M\cdot 2^W$ .
Gdzie $Z\in\nawiasw{-1, 1}$ jest znakiem liczby, $M\in\left[1,2 \right)$ jest mantysą,
natomiast $W\in\ZZ$ jest wykładnikiem.

Dzieląc dwie liczby $a_1 = Z_1\cdot M_1\cdot 2^{W_1}$ , $a_2 = Z_2\cdot M_2\cdot 2^{W_2}$
zmiennoprzecinkowe mamy $\frac{a_1}{a_2} = \frac{Z_1M_1}{Z_2M_2}\cdot 2^{W_1 - W_2}$
Widzimy zatem, że dzielenie liczb zmiennoprzecinkowych sprowadza się do dzielenia ich
mantys, gdzie każda z nich jest liczbą z przedziału $\left[1, 2\right)$ oraz odejmowania
wykładników. Wynik ilorazu znajduje się w przedziale $\left[ \frac{1}{2}, 2\right)$ .
Możliwe zatem, że wymagana będzie normalizacja. Przykładowo $0,7 = 1,4\cdot 2^{-1}$ .
Wówczas do różnicy wykładników trzeba odjąć jeszcze to 1. Do algorytmu nie musimy
wprowadzać żadnych modyfikacji. Nawet możemy do algorytmu podawać te mantysy z dołożonym
znakiem liczb $a_1, a_2$ , gdyż $Z\cdot M \in \left(-2, -1 \right] \cup \left[1, 2\right)$ .
Gdy dzielna i dzielnik są w tej postaci to iloraz będzie liczbą z przedziału
$\frac{a}{b}\in\left( -2, -\frac{1}{2} \right] \cup \left[ \frac{1}{2}, 2 \right)$ ,