Dawno dawno temu w starożytnym Egipcie żył sobie Marek. Marek wziął sobie trójkąt prostokątny, czyli taki, który ma kąt prosty.

Dla łatwiejszego formułowania myśli oznaczył sobie te boki przez , które w dodatku oznaczały także długość boków trójkąta.

Po czym zaczął wypisywać stosunki między długościami tych boków okazało, że jest ich 6, wypisał

   

Przy okazji zrozumiał także dlaczego jest ich 6. No bo stosunek to dzielenie dwóch wielkości . Jedną z tych liter mogę wybrać na 3 sposoby, bo mam 3 boki. Natomiast drugą na 2 sposoby no bo pozostaną mi dwa boki do wyboru.

Po chwili Marek narysował trójkąt podobny, (akurat wyszedł mu większy trójkąt) – no skoro podobny to miał takie same kąty jak poprzedni trójkąt.

Boki tego nowego trójkąta oznaczył odpowiednio przez . i siłą rzeczy miał nowe 6 stosunków.

Po chwili pomyślunku w tajemniczych okolicznościach spostrzegł, że stosunek w jednym trójkącie jest równy stosunkowi w nowym trójkącie. Pomyślał jako to przecież ten trójkąt jest większy? A po chwili zdał sobie sprawę, że to tak samo jak z

   

W tym momencie zaciekawiony zauważył, iż pozostałe stosunki także są sobie równe i zdał sobie sprawę, że rozmiar nie ma znaczenia, (trójkąta oczywiście 🙂

Nie mógł uwierzyć w to co zobaczył pobudzony narysował jeszcze inne podobne trójkąty i ciągle zachodziła równość. Zafascynowany chciał wykazać, że zawsze tak będzie szukał więc sposobu by to udowodnić. Po krótkiej chwili znalazł szybko sposób by to wykazać. Marek zarysował dwa trójkąty w taki sposób wówczas miał natychmiast wniosek z Twierdzenie Talesa, które już znał i kiedyś już dowodził.

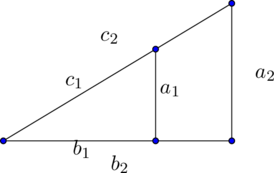
Miał natychmiast niezaprzeczalne uzasadnienie swojej hipotezy.

Pomyślał jeszcze dalej skoro stosunek nie zależy od wielkości trójkąta – to od czego zależy, no bo od czegoś musi zależeć. Przecież te trójkąty mają inne stosunki, boków.

Wtedy go uderzyło, że to musi zależeć od kątów. Wykonał jeszcze kilka rysunków by się upewnić w przekonaniu. Jednak pojawił się jeszcze moment zwątpienia i zmieszania.

W tym wypadku trójkąty maja te same kąty a stosunki są inne.

Tu już Marek szybko zdał sobie sprawę, że patrzy na te trójkąty od innej strony. Przecież boki, które brał z pierwszego są inaczej ułożone względem kątów niż boki brane z drugiego trójkąta.

Parę chwili później uściślił swoją myśl, że w zasadzie to zależą od jednego kąta no bo drugi można wyrazić przez pierwszy, jeden z nich jest zdeterminowany przez drugi, a przecież trzeci jest zawsze prosty.
Skoro w trójkącie suma kątów jest równa , czyli to

   

W końcu doszedł do takiego opisu trójkąta.

W tym momencie Marek miał już jak na dłoni najważniejszy wniosek w całych tych jego rozważaniach.

Marek czuł, że to co odkrył jest czymś ważnym. Głód wiedzy zżerał jego ciekawość co jeszcze można wywnioskować. Zaczął się zastanawiać JAK ten kąt wpływa na tę wartość tych stosunków, cóż to za związek, jak wygląda, jakie ma własności i czy jest to funkcja?

To były bardzo dobre pytania i faktycznie były to funkcje, no bo dla danego kąta mamy dokładnie jeden trójkąt z dokładnością do podobieństwa (skalowania), a one wszystkie mają ten sam stosunek. Teraz Marek już wiedział, że są to funkcję, miał ich 6. Trzy z nich to

   

a kolejne 3 są odwrotnościami tych 3 pierwszych

   

Marek czuł przeświadczenie, że to co odkrył jest ważne. Chciał te funkcje nazwać jakoś wyjątkowo, po chwili wymyślił nazwy dla pierwszych 3. Były to odpowiednio

Później uznał, że dla proporcji odwrotnych także wymyśli nazwy choć nie były już konieczne, bo przecież są odwrotnościami tych 3 pierwszych jednak zrobił to i kolejne funkcje nazwał

Jednak, gdy używał tych nazwy to okazały się zbyt długie by je pisać wielokrotnie i wymyślił skróty

W tym momencie dotarliśmy do tego co do dzisiaj podaje się w książkach.

*** QuickLaTeX cannot compile formula:

\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=0.6944444444444444cm,y=0.5567928730512249cm]

%\clip(-4.3,-2.68) rectangle (7.22,6.3);
\draw [shift={(0.,0.)},color=qqwuqqw,fill=qqwuqqw,fill opacity=0.1] (0,0) -- (0.:1.5) arc (0.:36.869897:1.5) -- cycle;
  \draw (0.,0.)-- (4.,0.);
  \draw (4.,0.)-- (4.,3.);
  \draw (4.,3.)-- (0.,0.);
  \draw [fill=qqqqff] (0.,0.) circle (1.5pt);
  \draw [fill=qqqqff] (4.,0.) circle (1.5pt);
  \draw [fill=qqqqff] (4.,3.) circle (1.5pt);
  \draw[color=qqwuqqw] (1.14,0.315) node {$\alpha$};
  \draw[color=black] (2.06,-0.26) node {$b$};
  \draw[color=black] (4.38,1.66) node {$a$};
  \draw[color=black] (1.86,1.92) node {$c$};
\end{tikzpicture}


*** Error message:
Command \degre already defined.
leading text: \newcommand{\degre}{\ensuremath{^\circ}}
Extra \endgroup. (in macro \document)
leading text: \begin{document}
Package xcolor Error: Undefined color `qqqqff'.
leading text: ...aw [fill=qqqqff] (0.,0.) circle (1.5pt);
Missing \endcsname inserted.
leading text: ...aw [fill=qqqqff] (0.,0.) circle (1.5pt);
Incomplete \ifx; all text was ignored after line 1223.
Emergency stop.

   

   

Comments

comments