Polecam wersje pdf tego artykułu jest lepiej sformatowana.
Postanowiłem napisać ten artykuł, gdyż materiały, z który to rozgryzałem nie były najlepsze. Często nie podawały wprost założeń jakie trzeba spełnić. Jak te ograniczenia obejść itp. W dodatku w języku polskim praktycznie nie ma materiałów na ten temat. Dlatego bardzo było by mi miło gdybyś napisał mi, czy i jak Ci ten materiał pomógł. Teraz do rzeczy.
Algorytm CORDIC pozwala na obliczenie wartości kilku funkcji matematycznych bez wykonywania mnożenia
- sinus
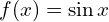
- kosinus
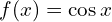
- arkus tangens
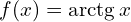
- sinus hiberboliczny
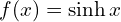
- kosinus hiberboliczny
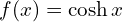
- area tangens hiberboliczny
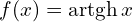
Pozwala także na obliczenie mnożenia i dzielenia bez wykonywania go wprost. Istnieją też różne modyfikacje pozwalające ponoć liczyć ![]() oraz
oraz ![]() ,
, ![]() i inne funkcje. Tego jednak nie sprawdzałem.
i inne funkcje. Tego jednak nie sprawdzałem.
Algorytm CORDIC jest pewną alternatywą dla szeregów Taylora. Opiera się tylko o dodawanie, odejmowanie, przesuwanie bitowe i potrzebuje pamięci aby spamiętać kilkanaście liczb. W tym miejscu już widać, że pierwszym wymaganiem jest to aby liczby były w postaci bitowej. Co w praktyce w zasadzie zawsze jest spełnione. Nie ma znaczenia czy operujemy na liczbach stałoprzecinkowych czy zmiennoprzecinkowych. Są jednak pewne ograniczenia co do zbieżności.
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|} \hline Nazwa funkcji & Przedział teoretyczny zbieżności & Sugerowane użycie \\ \hline $\sin x, \cos x$ & $x\in\nawias{-99,7\st; 99,7\st}$ & $x\in\nawias{-\frac{\pi}{2}, \frac{\pi}{2}}$ \\ \hline $\arctg x$ & $x\in \RR$ & $x\in \RR$ \\ \hline $a \cdot b$ & $a\in\RR, b\in\nawiask{-2,2}$ & $a,b\in\nawias{-2, 2}$ \\ \hline $\frac{a}{b}$ & $a\in\RR, b\in \RR \wedge \frac{a}{b}\in\nawiask{-2,2}$& $a,b\in\left(-2,-1\right] \cup \left[1, 2\right)$ \\ \hline $\sinh x, \cosh x$ & $x\in \nawias{-1,11; 1,11}$ & $x\in\nawias{-1,11; 1,11}$ \\ \hline $\artgh x $ & $x\in \nawias{-1; 1}$ & $x\in\nawias{-1; 1}$ \\ \hline \end{tabular}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-263695e20904baddd2592ea186f2617b_l3.png)
Możliwości obliczeniowe po połączeniu poszczególnych wariantów algorytmu, skorzystaniu z tożsamości matematycznych lub innych modyfikacjach.
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|} \hline Nazwa funkcji & Przedział rozszerzony & W jaki sposób \\ \hline $\sin x, \cos x$ & $x\in \RR$ & \begin{tabular}{@{}c@{}}trygonometryczne wzory \\ redukcyjne\end{tabular} \\ \hline $a \cdot b$ & $a,b\in\RR$ & \begin{tabular}{@{}c@{}}wykorzystanie własności \\ liczby zmiennoprzecinkowej \end{tabular} \\ \hline $\frac{a}{b}$ & $a,b\in\RR \wedge b \neq 0$ & \begin{tabular}{@{}c@{}}wykorzystanie własności \\ liczby zmiennoprzecinkowej\end{tabular} \\ \hline $\sinh x, \cosh x$ & $x\in \RR$ & \begin{tabular}{@{}c@{}}rekurencyjne wykorzystanie \\ tożsamości i mnożenia \\ $\sinh 2x = 2\sinh x \cosh x$ \\ $\cosh 2x = \cosh^2 x + \sinh^2 x$ \end{tabular}\\ \hline \end{tabular}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1e5006dd6d3d0a99b7d3e3ffedf06ec9_l3.png)
Dla funkcji sinus i kosinus szczególne kąty typu: ![]()
wykryć i potraktować oddzielnie.
Algorytm oblicza funkcję sinus i kosinus jednocześnie. Jest zatem szczególnie przydatny podczas obliczań obrotów na płaszczyźnie lub w przestrzeni trójwymiarowej. Nie jestem pewny, ale prawdopodobnie w kartach graficznych może być stosowany.Ponadto może być bardzo użyteczny w sprzęcie, w którym nie mamy do dyspozycji układów
mnożących. Grupą szczególnie zainteresowanych będą programiści niskopoziomowi, elektronicy i mikroelektronicy.
Co ciekawe Algorytm CORDIC pozwala także na obliczanie mnożenia i dzielenia bez wykonywania mnożenia i dzielenia. Tu także są pewne ograniczenia, ale poprzez odpowiednie użycie można je obejść. Oczywiście dzięki temu możemy w sytuacjach koniecznych wykonać mnożenie nie wykonując mnożenia wprost.
W przypadku funkcji hiperbolicznych ![]() oraz
oraz ![]() przedział zbieżności jest ograniczony tylko do około
przedział zbieżności jest ograniczony tylko do około ![]() . Można podać skąd te wartości pochodzą, ale jest to skomplikowane i nieistotne, bo i tak będę proponował zmniejszenie tego przedziału do
. Można podać skąd te wartości pochodzą, ale jest to skomplikowane i nieistotne, bo i tak będę proponował zmniejszenie tego przedziału do ![]() . Wykorzystując tożsamości matematyczne można to rozszerzyć na większy
. Wykorzystując tożsamości matematyczne można to rozszerzyć na większy
przedział, potrzebne jednak będzie wykonywanie mnożenia, które może być realizowane inną wersją/instancją algorytmu, tą wykonującą mnożenie bez mnożenia.
Algorytm CORDIC jest algorytmem iteracyjnym. Cechuje się tym, że kolejna iteracja niekoniecznie musi dać dokładniejszy wyniki, niż poprzednia. Co więcej na poprawę “rekordu” możemy krótko lub długo czekać. Jednak w długiej perspektywie algorytm jest zbieżny. Problem jednak polega na tym, że aby uniknąć mnożenia trzeba z góry założyć ile tych iteracji wykonamy.
Istnieje możliwość obliczenia dodatkowych funkcji matematycznych pośrednio.
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|} \hline Funkcja matematyczna & Uwagi \\ \hline $\tg x = \frac{\sin x}{\cos x}$ & trzeba dzielić \\ \hline $\ctg x = \frac{\cos x}{\sin x}$ & trzeba dzielić \\ \hline $\arcctg x = \frac{\pi}{2} - \arctg x$ & tylko odejmowanie \\ \hline $\arctg_2(y,x) = \begin{cases} \arctg \frac{y}{x} & \mbox{, } x > 0 \\ \arctg \frac{y}{x} + \pi & \mbox{, } x < 0 \wedge y\geq 0 \\ \arctg \frac{y}{x} - \pi & \mbox{, } x < 0 \wedge y < 0 \\ \frac{\pi}{2} & \mbox{, } x = 0 \wedge y > 0 \\ -\frac{\pi}{2} & \mbox{, } x = 0 \wedge y < 0 \\ \mbox{nieokreślone} & \mbox{, } x = 0 \wedge y = 0 \\ \end{cases}$ & dodawanie lub odejmowanie $\pi$ \\ \hline $\tgh x = \frac{\sinh x}{\cosh x} $ & trzeba dzielić \\ \hline $\ctgh x = \frac{\cosh x}{\sinh x} $ & trzeba dzielić \\ \hline $e^x = \sinh x + \cosh x $ & \begin{tabular}{@{}c@{}} tylko dodawanie, o ile mnożenia \\ nie było w samym $\sinh x$ lub $\cosh x$ \end{tabular} \\ \hline $\sqrt{x^2 + y^2}$ & trzeba mnożyć \\ \hline $\sqrt{x^2 - y^2}$ & trzeba mnożyć \\ \hline $\ln x = 2\artgh \frac{x-1}{x+1}$ & \begin{tabular}{@{}c@{}} trzeba dzielić, zauważmy, że \\ dla $x>0 \Leftrightarrow \frac{x-1}{x+1}\in\nawias{-1,1}$ \end{tabular} \\ \hline $\log_a x = \frac{\ln x}{\ln a}$ & trzeba dzielić \\ \hline $a^x = e^{x\ln a} $ & trzeba mnożyć \\ \hline $\sqrt{x} = \sqrt{\nawias{x+\frac{1}{4}}^2 - \nawias{x-\frac{1}{4}}^2}$ & trzeba mnożyć \\ \hline \end{tabular}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-dda4f6c46056bf70222005aa5da439a1_l3.png)
Skupmy się teraz tylko nad zasadą działania w trybie rotacyjnym. Pozwalającym obliczać sinus i kosinus. Tę zasadę zmodyfikujemy nieco w trybie wektorowym, która pozwoli nam obliczyć ![]()
Algorytm CORDIC w trybie rotacyjnym (rotation mode)
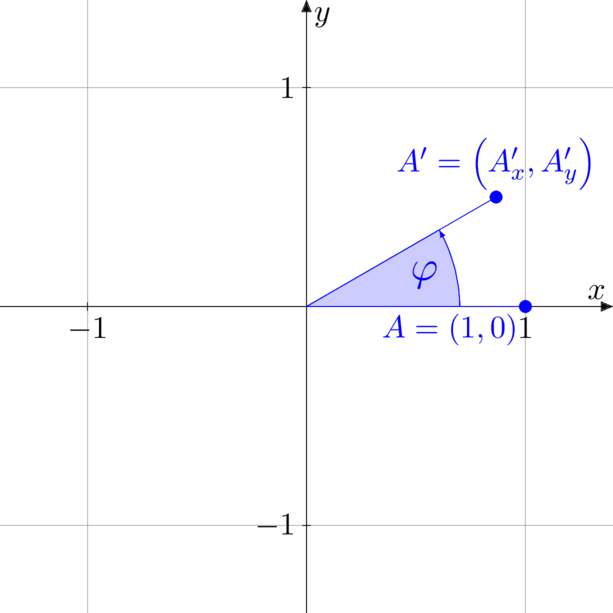
Obrót na płaszczyźnie o kąt  przy nieruchomym układzie współrzędnych
przy nieruchomym układzie współrzędnych
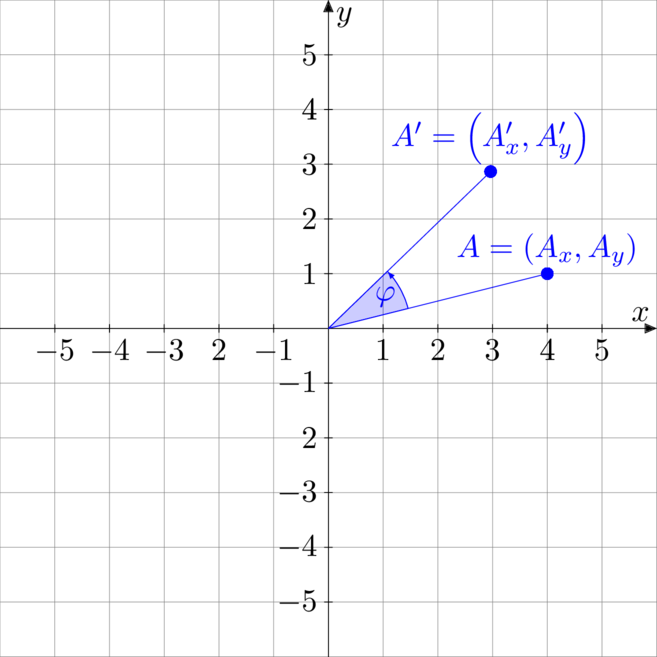
Przypomnijmy, że obrót na płaszczyźnie można zrealizować przy pomocy macierzy obrotu.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \\ \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a8c40ab449b2f82342e9c50035e8a37f_l3.png)
Chcąc obrócić punkt ![]() o kąt
o kąt ![]() w nieruchomym układzie współrzędnych, należy
w nieruchomym układzie współrzędnych, należy
![Rendered by QuickLaTeX.com \[\begin{bmatrix} A'_x \\ A'_y \end{bmatrix} = \begin{bmatrix} \cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \\ \end{bmatrix} \cdot \begin{bmatrix} A_x \\ A_y \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a17ee2876074d4c1b082aecd1b83a6bf_l3.png)
Zauważmy, że jeśli obracalibyśmy punkt o współrzędnych ![]() , to w wyniku obrotu otrzymamy punkt o współrzędnych
, to w wyniku obrotu otrzymamy punkt o współrzędnych ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \cos \varphi \\ \sin \varphi \end{bmatrix} = \begin{bmatrix} \cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \\ \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4b6c7366e14b643bb8ca2d7acdbd5c3f_l3.png)
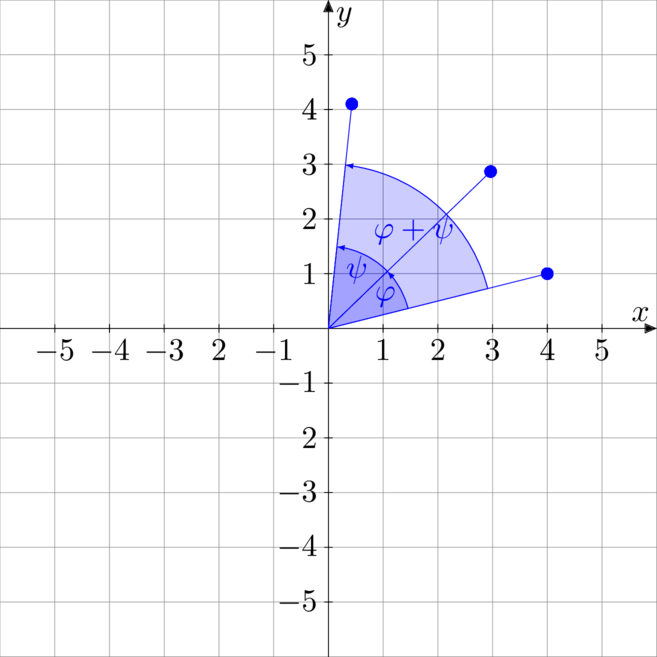
Wykonując kolejno dwa obroty, najpierw o kąt ![]() , a potem o kąt
, a potem o kąt ![]() skutek będzie taki sam jak wykonanie obrotu od razu o kąt
skutek będzie taki sam jak wykonanie obrotu od razu o kąt ![]() . Potwierdza to też rachunek macierzowy.
. Potwierdza to też rachunek macierzowy.
![Rendered by QuickLaTeX.com \[\begin{bmatrix} \cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \\ \end{bmatrix} \cdot \begin{bmatrix} \cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \\ \end{bmatrix} = \begin{bmatrix} \cos \nawias{\varphi + \psi} & -\sin \nawias{\varphi + \psi} \\ \sin \nawias{\varphi + \psi} & \cos \nawias{\varphi + \psi} \\ \end{bmatrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d9eb163e8d0547fef2fb69c5ed23833e_l3.png)
Przekształcenie
Wróćmy do dowolnego punktu ![]() . Efekt po obrocie zapiszmy w postaci układu równań.
. Efekt po obrocie zapiszmy w postaci układu równań.
![Rendered by QuickLaTeX.com \[\begin{cases} A'_x = A_x \cos \varphi - A_y \sin \varphi \\ A'_y = A_x \sin \varphi + A_y \cos \varphi \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8411c5527e929ac59f99ecfa18f3a39c_l3.png)
Jeżeli przyjmiemy, że wykonujemy obroty w ramach kątów![]() , to wówczas
, to wówczas ![]() . W takim razie można w prawych stronach wyciągnąć przed nawias
. W takim razie można w prawych stronach wyciągnąć przed nawias ![]() , a właściwie to za nawias.
, a właściwie to za nawias.
![Rendered by QuickLaTeX.com \[\begin{cases} A'_x = A_x \cos \varphi - A_y \sin \varphi \\ A'_y = A_x \sin \varphi + A_y \cos \varphi \\ \end{cases} \dalej \begin{cases} A'_x = \nawias{A_x - A_y\tg \varphi} \cos \varphi \\ A'_y = \nawias{A_y + A_x\tg \varphi} \cos \varphi \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4244ec05c3f8eab16f7b647bcd08b1f6_l3.png)
Zauważmy, że skoro ![]() , to zachodzi tożsamość
, to zachodzi tożsamość
![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{1 + \tg^2 \varphi}} = \frac{1}{\sqrt{ \frac{\cos^2 \varphi + \sin^2 \varphi}{\cos^2 \varphi}}} = \frac{1}{\frac{1}{|\cos \varphi|}} = |\cos \varphi| = \cos \varphi\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3753b50572030b3ebdaa46c7b7652068_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} A'_x = \nawias{A_x - A_y\tg \varphi} \cos \varphi \\ A'_y = \nawias{A_y + A_x\tg \varphi} \cos \varphi \\ \end{cases} \dalej \begin{cases} A'_x = \nawias{A_x - A_y\tg \varphi} \frac{1}{\sqrt{1 + \tg^2 \varphi}} \\ A'_y = \nawias{A_y + A_x\tg \varphi} \frac{1}{\sqrt{1 + \tg^2 \varphi}} \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-b576218361319ec8236a8168c33a1060_l3.png)
Obrót jako suma mniejszych obrotów
Jeżeli kąt ![]() zapiszemy jako sumę
zapiszemy jako sumę ![]() innych kątów, tzn.
innych kątów, tzn.
![Rendered by QuickLaTeX.com \[\varphi = \varphi_0 + \varphi_1 + \varphi_2 + \ldots + \varphi_{n-1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-63822b91da38d3634951510b09592e54_l3.png)
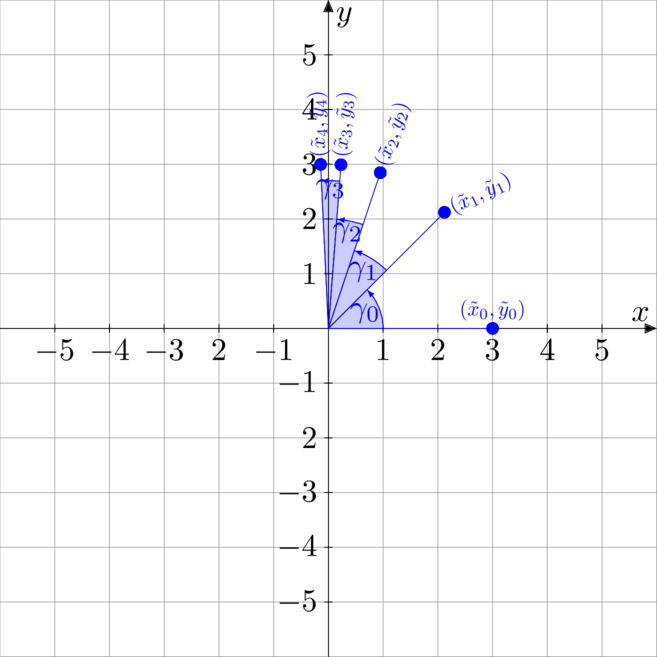
To wówczas można zapisać następujący układ rekurencji, którego każda iteracja odpowiada za obrót punktu ![]() o kąt
o kąt ![]() . %, czyli innymi słowy równania różnicowe
. %, czyli innymi słowy równania różnicowe
![Rendered by QuickLaTeX.com \[\begin{cases} \tilde{x}_{k + 1} = \nawias{\tilde{x}_k - \tilde{y}_k\tg \varphi_k} \frac{1}{\sqrt{1 + \tg^2 \varphi_k}} \\ \tilde{y}_{k + 1} = \nawias{\tilde{y}_k + \tilde{x}_k\tg \varphi_k} \frac{1}{\sqrt{1 + \tg^2 \varphi_k}} \\ \tilde{x}_0 = A_x \\ \tilde{y}_0 = A_y \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-0934ad656305c781a2e380a9f20af7c7_l3.png)
Po ![]() krokach otrzymujemy dobre przybliżenie obrazu punktu
krokach otrzymujemy dobre przybliżenie obrazu punktu ![]() czyli punkt
czyli punkt ![]() . Zauważmy, że funkcja
. Zauważmy, że funkcja ![]() jest funkcją nieparzystą, tzn.
jest funkcją nieparzystą, tzn. ![]() . Zatem jeśli znamy
. Zatem jeśli znamy ![]() dla pewnego
dla pewnego ![]() to znamy także
to znamy także ![]() dla
dla ![]() . Wystarczy zmienić znak
. Wystarczy zmienić znak ![]() na przeciwny. Zastanówmy się nad zbiorem takich kątów
na przeciwny. Zastanówmy się nad zbiorem takich kątów ![]() , które dodając lub odejmując mogłyby
, które dodając lub odejmując mogłyby
zbliżyć się dowolnie blisko zadanemu kątowi ![]() przy odpowiednio dużej liczbie kroków.
przy odpowiednio dużej liczbie kroków.
Widzimy, że w każdej iteracji trzeba wykonać mnożenie ![]() z
z ![]() . Chcemy uniknąć mnożenia. Jedyne na co się godzimy to mnożenie przez potęgę 2 tzn. przez
. Chcemy uniknąć mnożenia. Jedyne na co się godzimy to mnożenie przez potęgę 2 tzn. przez ![]() , gdzie
, gdzie ![]() . Mnożenie liczby
. Mnożenie liczby ![]() w systemie dwójkowym przez
w systemie dwójkowym przez ![]() odpowiada przesuwaniu bitów liczby
odpowiada przesuwaniu bitów liczby ![]() w lewo lub w prawo. Jeśli
w lewo lub w prawo. Jeśli ![]() jest dodatnie to wówczas przesuwamy bity w lewo o
jest dodatnie to wówczas przesuwamy bity w lewo o ![]() pozycji. Jeśli
pozycji. Jeśli ![]() jest ujemne wówczas przesuwamy bity w prawo o
jest ujemne wówczas przesuwamy bity w prawo o ![]() pozycji. Niech zatem to będzie taki zbiór kątów, dla których
pozycji. Niech zatem to będzie taki zbiór kątów, dla których ![]() będzie potęgą 2. Rozpatrzmy zbiór kątów dla, których
będzie potęgą 2. Rozpatrzmy zbiór kątów dla, których ![]() , gdzie
, gdzie ![]() jest liczba naturalną. Matematycznie taki zbiór można zapisać tak:
jest liczba naturalną. Matematycznie taki zbiór można zapisać tak:
![Rendered by QuickLaTeX.com \[\nawiasw{\gamma_k \in \left( 0, \frac{\pi}{4} \right] : \gamma_k = \arctg 2^{-k} \quad \wedge \quad k\in \NN }\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-87713bd920b44d956f744e0e4f65fd4c_l3.png)
Gdybyśmy z góry wcześniej wyznaczyli wartości tych kątów do pewnego niekoniecznie dużego ![]() , np.
, np. ![]() i je zapamiętali, to wówczas zamiast wykonywać kosztowne mnożenie przesuwalibyśmy bity liczby.
i je zapamiętali, to wówczas zamiast wykonywać kosztowne mnożenie przesuwalibyśmy bity liczby.
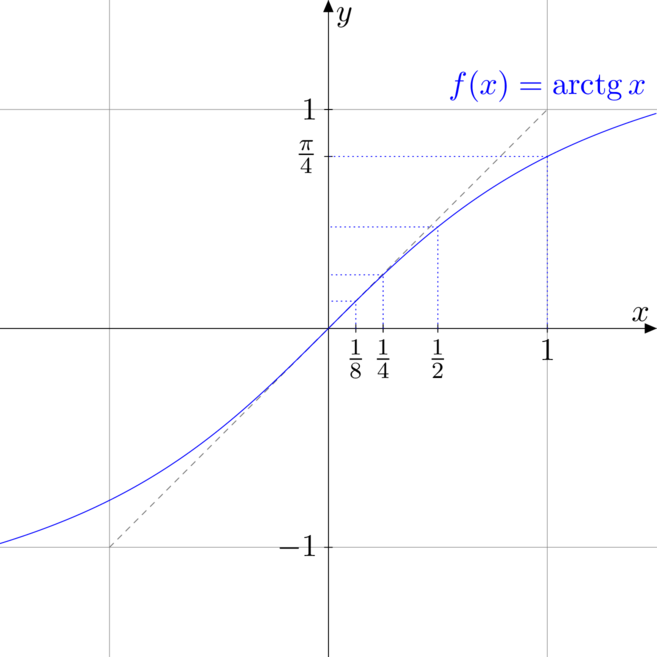
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|} \hline $k$ & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & \ldots \\ \hline $\gamma_k$ &$\arctg 1$ &$\arctg\frac{1}{2}$ &$\arctg\frac{1}{4}$ &$\arctg\frac{1}{8}$ &$\arctg\frac{1}{16}$ &$\arctg\frac{1}{32}$ &$\arctg\frac{1}{64}$ &$\arctg\frac{1}{128}$ &$\arctg\frac{1}{256}$ & \ldots \\ \hline $\gamma_k$ &$45,0\st$ &$26,57\st$ &$14,04\st$ &$7,13\st$ &$3,58\st$ &$1,79\st$ &$0,9\st$ &$0,45\st$ &$0,22\st$ & \ldots \\ \hline $\gamma_k$ & 0,785 & 0,464 & 0,245 & 0,124 & 0,062 & 0,031 & 0,016 & 0,008 & 0,004 & \ldots \\ \hline \end{tabular}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-537d9bac31bf69aac3a20fcfa9c5045e_l3.png)
![Rendered by QuickLaTeX.com \[\varphi_k = \epsilon_k\gamma_k, \quad \mbox{gdzie} \quad \epsilon_k \in \nawiasw{-1, 1}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-08eb8a3550396099685e604cf4bfd5e3_l3.png)
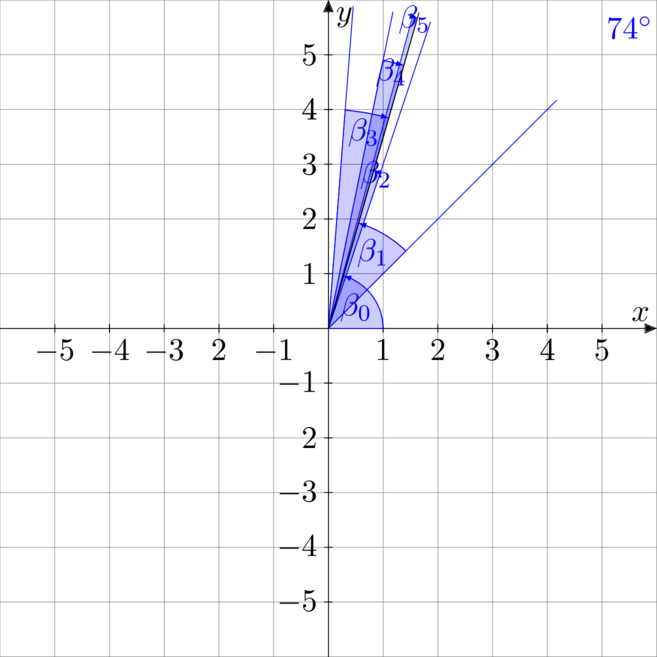
Należy się zastanowić czy każdy kąt z przedziału ![]() można przestawić jako sumę tych kątów, gdzie dany kąt może być wzięty z plusem lub z minusem. Przykładowo kąt
można przestawić jako sumę tych kątów, gdzie dany kąt może być wzięty z plusem lub z minusem. Przykładowo kąt
![Rendered by QuickLaTeX.com \[74\st \approx \gamma_0 + \gamma_1 + \gamma_2 - \gamma_3 - \gamma_4 - \gamma_5 + \gamma_6\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ad2a7773f174bb86b6d74bcb0e52b6dd_l3.png)
![Rendered by QuickLaTeX.com \[74\st \approx 45,0\st + 26,57\st + 14,04\st - 7,13\st - 3,58\st - 1,79\st + 0,9\st\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-1d0b4cb11b004682baa2ff45184c58bd_l3.png)
Dla każdego kąta można znaleźć taki ciąg plusów i minusów jaki należy dołożyć do kątów![]() aby ten ciąg dążył do zadanego kąta. Pozostawiam to bez dowodu.
aby ten ciąg dążył do zadanego kąta. Pozostawiam to bez dowodu.
Warto zaznaczyć, że w długiej perspektywie iteracji wyniki się poprawiają, lecz w krótkim zakresie parę kolejnych iteracji może dać gorszy wynik zanim trafimy na iterację, która wynik poprawi.
Pojawia się pytanie jak wybierać te znaki? Odpowiedź jest prostsza, niż się wydaje. Jak aktualnie naliczona suma kątów ![]() jest mniejsza od szukanego kąta
jest mniejsza od szukanego kąta ![]() to następny kąt
to następny kąt ![]() trzeba dodać. Jak bieżąca suma jest większa od danego kąta
trzeba dodać. Jak bieżąca suma jest większa od danego kąta ![]() to następny kąt
to następny kąt ![]() trzeba odjąć.
trzeba odjąć.
Tę zasadę można odwrócić i dany kąt ![]() z kroku na krok modyfikować, aż będzie dostatecznie blisko 0 lub gdy uznamy, że osiągnęliśmy maksymalną liczbę kroków
z kroku na krok modyfikować, aż będzie dostatecznie blisko 0 lub gdy uznamy, że osiągnęliśmy maksymalną liczbę kroków ![]() . Niech
. Niech ![]() oznacza kąt, po kroku
oznacza kąt, po kroku ![]() , jaki pozostał jeszcze do obrócenia, aby znaleźć się w punkcie
, jaki pozostał jeszcze do obrócenia, aby znaleźć się w punkcie ![]() , będącym obrazem punkt
, będącym obrazem punkt ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{cases} %\beta_{k + 1} = \beta_{k} - \underbrace{\sgn(\beta_k)}_{\epsilon_k} \gamma_k \\ \beta_{k + 1} = \beta_{k} - \varphi_k \\ \beta_0 = \varphi \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6b8b8565092be0d1d16f710121366f6f_l3.png)
Gdzie po ![]() krokach
krokach ![]() . Zauważmy także, że
. Zauważmy także, że ![]() , a co za tym idzie
, a co za tym idzie
![Rendered by QuickLaTeX.com \[\tg \varphi_k = \tg (\epsilon_k \gamma_k) = \epsilon_k\tg \gamma_k = \sgn(\beta_k)\tg \gamma_k = \sgn(\beta_k)2^{-k}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-5d9541a63380f4c82074e6eea8c5d579_l3.png)
W ten sposób problem mnożenia ![]() oraz
oraz![]() został rozwiązany. Pozostała kwestia
został rozwiązany. Pozostała kwestia
mnożenia przez ![]() .
.
Mnożenie przez 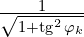
Zaobserwujmy co się dzieje podczas dwóch kolejnych iteracji.
![Rendered by QuickLaTeX.com \[\begin{cases} \tilde{x}_{1} = \nawias{\tilde{x}_0 - \tilde{y}_0\tg \varphi_0} \frac{1}{\sqrt{1 + \tg^2 \varphi_0}} \\ \tilde{y}_{1} = \nawias{\tilde{y}_0 + \tilde{x}_0\tg \varphi_0} \frac{1}{\sqrt{1 + \tg^2 \varphi_0}} \\ \end{cases} \dalej \begin{cases} \tilde{x}_{2} = \nawias{\tilde{x}_1 - \tilde{y}_1\tg \varphi_1} \frac{1}{\sqrt{1 + \tg^2 \varphi_1}} \\ \tilde{y}_{2} = \nawias{\tilde{y}_1 + \tilde{x}_1\tg \varphi_1} \frac{1}{\sqrt{1 + \tg^2 \varphi_1}} \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bb639df303ae6448e90b6c3eb2f71d30_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} \tilde{x}_{2} = \nawiask{\nawias{\tilde{x}_0 - \tilde{y}_0\tg \varphi_0} - \nawias{\tilde{y}_0 + \tilde{x}_0\tg \varphi_0}\tg \varphi_1} \frac{1}{\sqrt{1 + \tg^2 \varphi_0}\sqrt{1 + \tg^2 \varphi_1}} \\ \tilde{y}_{2} = \nawiask{\nawias{\tilde{y}_0 + \tilde{x}_0\tg \varphi_0} + \nawias{\tilde{x}_0 - \tilde{y}_0\tg \varphi_0}\tg \varphi_1} \frac{1}{\sqrt{1 + \tg^2 \varphi_0}\sqrt{1 + \tg^2 \varphi_1}} \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ca2303bc0fc213c7397cf9f570fac735_l3.png)
Możemy zatem skupić się na rekurencji poniżej, w której po wykonaniu ![]() iteracji otrzymamy przybliżenie obraz punkt
iteracji otrzymamy przybliżenie obraz punkt ![]() , czyli punkt
, czyli punkt ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{cases} x_{k + 1} = x_{k} - y_{k}\tg \varphi_{k} \\ y_{k + 1} = y_{k} + x_{k}\tg \varphi_{k} \\ x_{0} = A_x \\ y_{0} = A_y \\ \end{cases} \quad \to \quad \begin{cases} %A'_x \approx \tilde{x}_{n} = x_{n} \prod\limits_{k = 0}^{n - 1} \frac{1}{\sqrt{1 + \tg^2 \varphi_k}} \\ %A'_y \approx \tilde{y}_{n} = y_{n} \prod\limits_{k = 0}^{n - 1} \frac{1}{\sqrt{1 + \tg^2 \varphi_k}} \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-8a6d133871afe4f3761395de2c19dbd0_l3.png)
Zauważmy iż ![]() , oznacza to, że wszystkie
, oznacza to, że wszystkie ![]() są znane z góry, bo znane są z góry wartości kątów
są znane z góry, bo znane są z góry wartości kątów ![]() , tzn.
, tzn. ![]() nie zależy od wybrania
nie zależy od wybrania ![]() .
.
Rozpatrzmy funkcję ![]() , która w zasadzie jest ciągiem, którego pierwszy wyraz jest o indeksie 1. Ciąg jest dany wzorem
, która w zasadzie jest ciągiem, którego pierwszy wyraz jest o indeksie 1. Ciąg jest dany wzorem
![Rendered by QuickLaTeX.com \[K_n = \prod\limits_{k = 0}^{n - 1} \frac{1}{\sqrt{1 + \tg^2 \varphi_k}} = \frac{1}{\sqrt{\prod\limits_{k = 0}^{n-1} \nawias{1 + \tg^2 \varphi_k }}} = \frac{1}{\sqrt{\prod\limits_{k = 0}^{n-1} \nawias{1 + 2^{-2k} }}}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-fd86280dd1ba8595639a56bbab8f575c_l3.png)
Można policzyć jednokrotnie wyrazy tego ciągu i zapamiętać.
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|} \hline $n$ & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & \ldots \\ \hline $K_n$ & 0,7071 & 0,6325 & 0,6135 & 0,6088 & 0,6076 & 0,6074 & 0,6073 & 0,6073 & \ldots \\ \hline \end{tabular}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-d2a8def84f8ed9428f931988c634d1cc_l3.png)
Zamiast obliczać rekurencję z ![]() i
i ![]() możemy obliczać rekurencję z
możemy obliczać rekurencję z ![]() oraz
oraz ![]() , a na koniec raz pomnożyć przez
, a na koniec raz pomnożyć przez ![]() .
.
Wygląda na to, że jednego mnożenia trzeba będzie zatem dokonać.
Okazuje się, że jednak tego mnożenia także można uniknąć.
Zauważmy, że zamiast mnożyć na końcu to można by mnożyć na początku.
Wywnioskować to można spoglądając na rozpisane wcześniej 2 iteracje.
![Rendered by QuickLaTeX.com \[\begin{matrix} \begin{cases} x_{k + 1} = x_{k} - y_{k}\tg \varphi_{k} \\ y_{k + 1} = y_{k} + x_{k}\tg \varphi_{k} \\ x_{0} = \tilde{x}_0 = A_x \\ y_{0} = \tilde{y}_0 = A_y \\ \end{cases}\\ \begin{cases} %x_{n} = \tilde{x}_{n} \prod\limits_{k = 0}^{n - 1} \frac{1}{\sqrt{1 + \tg^2 \varphi_k}} \\ %y_{n} = \tilde{y}_{n} \prod\limits_{k = 0}^{n - 1} \frac{1}{\sqrt{1 + \tg^2 \varphi_k}} \\ \tilde{x}_{n} = x_{n} K_{n} \\ \tilde{y}_{n} = y_{n} K_{n} \\ \end{cases} \end{matrix} \quad \to \quad \begin{matrix} \begin{cases} x_{k + 1} = x_{k} - y_{k}\tg \varphi_{k} \\ y_{k + 1} = y_{k} + x_{k}\tg \varphi_{k} \\ x_{0} = \tilde{x}_0 = A_x K_{n} \\ y_{0} = \tilde{y}_0 = A_y K_{n} \\ \end{cases} \\ \begin{cases} \tilde{x}_{n} = x_{n} \\ \tilde{y}_{n} = y_{n} \\ \end{cases} \end{matrix}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-4411d2468ee14ee2800d867e79b1d79d_l3.png)
Możemy przestać skupiać się na zmiennych akcentowanych tyldą ![]() oraz
oraz ![]() , a skupić na zmiennych nieakcentowanych tyldą, czyli
, a skupić na zmiennych nieakcentowanych tyldą, czyli ![]() oraz
oraz ![]() . Jak już było wspomniane
. Jak już było wspomniane ![]()
![Rendered by QuickLaTeX.com \[\begin{cases} x_{k + 1} = x_{k} - y_{k}\tg \varphi_{k} \\ y_{k + 1} = y_{k} + x_{k}\tg \varphi_{k} \\ \beta_{k + 1} = \beta_{k} - \sgn(\beta_k)\gamma_k \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \beta_0 = \varphi\\ \end{cases} \quad \to \quad \begin{cases} x_{k + 1} = x_{k} - \sgn(\beta_k)y_{k}2^{-k} \\ y_{k + 1} = y_{k} + \sgn(\beta_k)x_{k}2^{-k} \\ \beta_{k + 1} = \beta_{k} - \sgn(\beta_k)\gamma_k \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \beta_0 = \varphi\\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-94c2a25cda79becec619d0f34efb961c_l3.png)
życie algorytmu w celu obliczenia 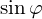 oraz
oraz 
Teraz tak jak powiedziane było na początku. Jeśli punkt ![]() będzie punktem
będzie punktem ![]() to w wyniku otrzymamy punkt o współrzędnych
to w wyniku otrzymamy punkt o współrzędnych ![]() . Decydując się na konkretną liczbę iteracji np.
. Decydując się na konkretną liczbę iteracji np. ![]() z góry wiadomo, że
z góry wiadomo, że
![Rendered by QuickLaTeX.com \[\begin{cases} x_{0} = K_{n} \\ y_{0} = 0 \\ \beta_0 = \varphi\\ \end{cases}.\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-6780165e36d4bfd31b4509eb43014d17_l3.png)
Ograniczeniem jest to, że z góry na starcie musimy zdecydować ile zrobimy iteracji tego algorytmu. W ten sposób utworzyliśmy równania rekurencyjne, które pozwalają jednocześnie obliczyć wartość funkcji sinus i kosinus dla dowolnego kąta. Wzorami redukcyjnymi sprowadzamy dowolny kąt do kąta z przedziału ![]() , a następnie wykonujemy
, a następnie wykonujemy ![]() iteracji poniższego układu. %równań.
iteracji poniższego układu. %równań.
![Rendered by QuickLaTeX.com \[\begin{cases} x_{k + 1} = x_{k} - \sgn(\beta_k)y_{k}2^{-k} \\ y_{k + 1} = y_{k} + \sgn(\beta_k)x_{k}2^{-k} \\ \beta_{k + 1} = \beta_{k} - \sgn(\beta_k)\gamma_k \\ x_{0} = K_{n} \\ y_{0} = 0 \\ \beta_0 = \varphi\\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-441877e2b44addb52e8cf2dfa03b4c21_l3.png)
Przybliżone wartości funkcji sinus i kosinus to
![Rendered by QuickLaTeX.com \[\begin{cases} \cos \varphi \approx x_k \\ \sin \varphi \approx y_k \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-efba721432587750cdd74ba3b48eac7b_l3.png)
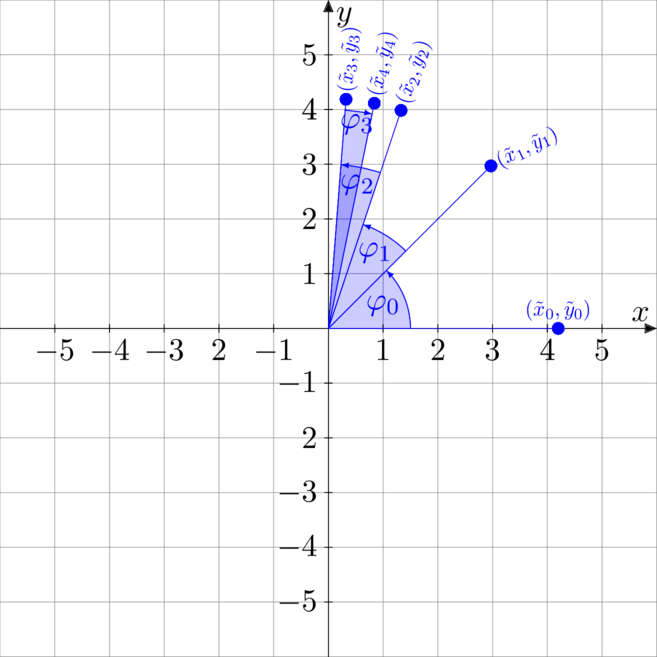
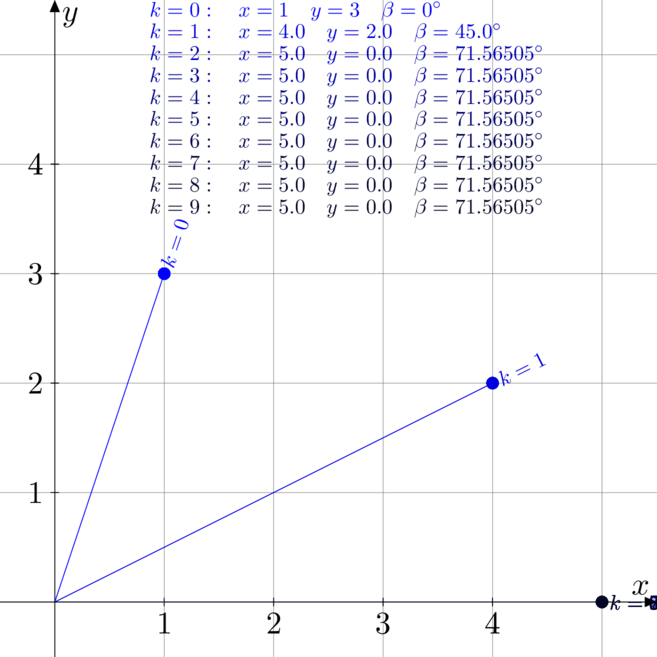
Przykłady trybu rotacyjnego
Poniżej zwizualizowane i rozpisane są dwa przykłady. Jeden dotyczy obliczania ![]() oraz
oraz ![]() , a drugi obliczenia
, a drugi obliczenia ![]() oraz
oraz ![]()
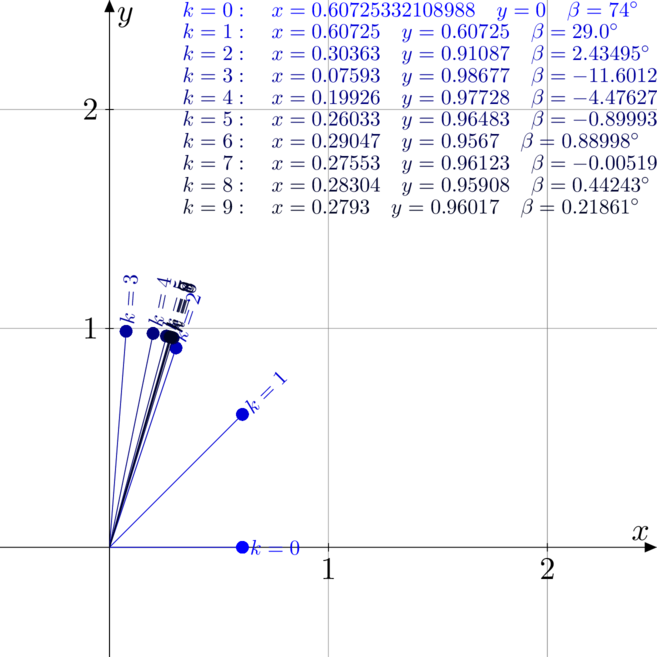
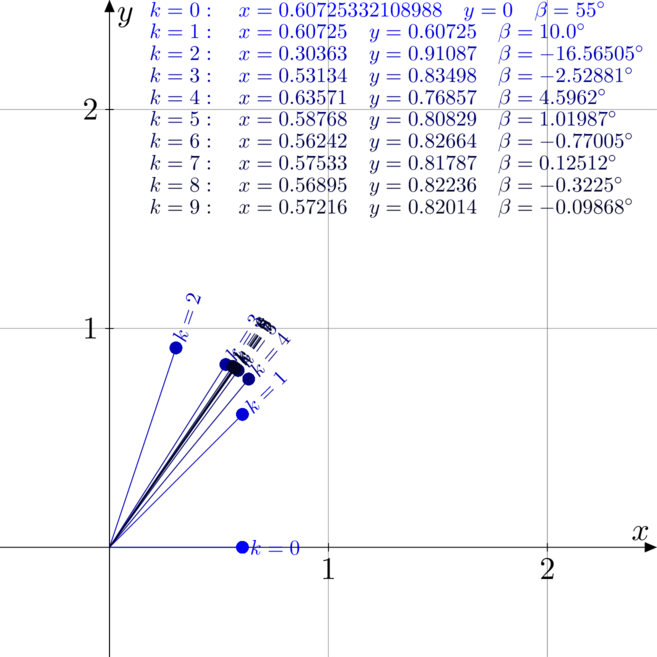
Algorytm CORDIC w trybie wektorowym (vectoring mode)
W trybie rotacyjnym zadany punkt ![]() był obracany kolejno przez kąty
był obracany kolejno przez kąty ![]() , dla
, dla ![]() , aż osiągnięty zostanie punkt
, aż osiągnięty zostanie punkt ![]() . W trybie wektorowym zaczynam od dowolnego punktu
. W trybie wektorowym zaczynam od dowolnego punktu ![]() , dla którego nie znamy kąta
, dla którego nie znamy kąta ![]() . Obracamy o kolejne kąty
. Obracamy o kolejne kąty ![]() aż współrzędna
aż współrzędna ![]() obrazu będzie w przybliżeniu równa
obrazu będzie w przybliżeniu równa ![]() . Współrzędna
. Współrzędna ![]() obrazu będzie wówczas równa
obrazu będzie wówczas równa ![]() , wynika to z twierdzenia Pitagorasa. Tryb wektorowy pozwala na obliczenie wartości funkcji
, wynika to z twierdzenia Pitagorasa. Tryb wektorowy pozwala na obliczenie wartości funkcji ![]() , a dokładniej to
, a dokładniej to ![]() . Wyjdźmy od postaci
. Wyjdźmy od postaci
![Rendered by QuickLaTeX.com \[\begin{cases} x_{k + 1} = x_{k} - y_{k}\tg \varphi_{k} \\ y_{k + 1} = y_{k} + x_{k}\tg \varphi_{k} \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-601c6c7598c2ed9ed572048c8076cb20_l3.png)
Zauważmy, że dla kątów ![]() ,
,
współrzędna ![]() to o jaki kąt należy obrócić w danej iteracji zależy
to o jaki kąt należy obrócić w danej iteracji zależy
od znaku ![]() . Kąt obrotu w danej iteracji to
. Kąt obrotu w danej iteracji to ![]() . Jeżeli
. Jeżeli ![]() jest dodatnie to należy obrócić o kąt
jest dodatnie to należy obrócić o kąt ![]() ujemny. Jak
ujemny. Jak ![]() jest ujemne to należy obrócić o kąt
jest ujemne to należy obrócić o kąt ![]() dodatni. Wynika nam z tego
dodatni. Wynika nam z tego
![Rendered by QuickLaTeX.com \[\varphi_k = \epsilon_k \gamma_k = -\sgn(y_k) \gamma_k\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-bac83dbcaffd568d2fa5901b097a6e8a_l3.png)
Natomiast kąt ![]() to będzie suma wykonanych obrotów
to będzie suma wykonanych obrotów ![]()
z przeciwnym znakiem. Jest tak dla tego, że suma katów obrotu sprowadzenia punkt ![]() do punkt
do punkt ![]() jest kątem o przeciwnym zwrocie do kąta od dodatniej półosi osi
jest kątem o przeciwnym zwrocie do kąta od dodatniej półosi osi ![]() do promienia wodzącego
do promienia wodzącego ![]() . Otrzymujemy następująca rekurencję
. Otrzymujemy następująca rekurencję
![Rendered by QuickLaTeX.com \[\begin{cases} \beta_{k + 1} = \beta_k - \varphi_k\\ \beta_0 = 0\\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-9bfa5dbb4fb0b3c7c4e94490a68d9791_l3.png)
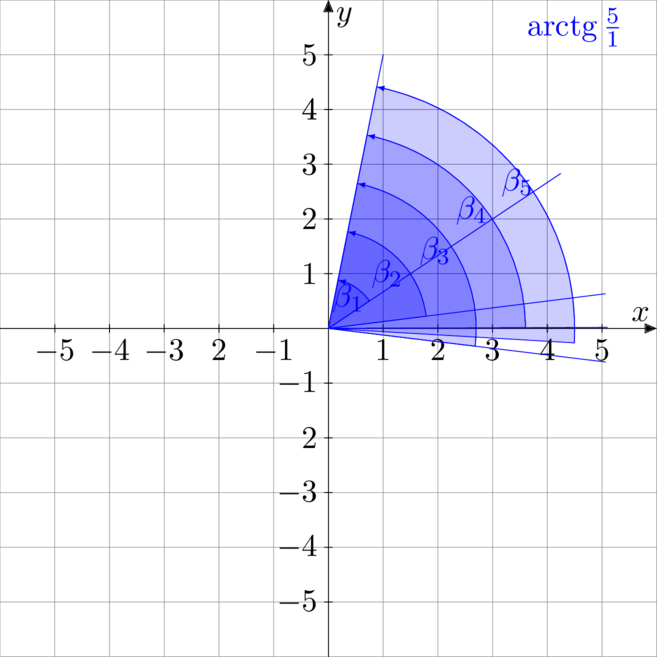
Układ rekurencji dla tego algorytmu jest następujący
![Rendered by QuickLaTeX.com \[\begin{cases} x_{k + 1} = x_{k} - y_{k}\tg \varphi_{k} \\ y_{k + 1} = y_{k} + x_{k}\tg \varphi_{k} \\ \beta_{k + 1} = \beta_k - \varphi_k \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \beta_0 = 0 \\ \end{cases} \quad \to \quad \begin{cases} x_{k + 1} = x_{k} + \sgn(y_k) y_{k}\tg \gamma_k \\ y_{k + 1} = y_{k} - \sgn(y_k) x_{k}\tg \gamma_k \\ \beta_{k + 1} = \beta_k + \sgn(y_k)\gamma_k \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \beta_0 = 0 \\ \end{cases} \quad \to \quad \begin{cases} x_{k + 1} = x_{k} + \sgn(y_k) y_{k}2^{-k}\\ y_{k + 1} = y_{k} - \sgn(y_k) x_{k}2^{-k}\\ \beta_{k + 1} = \beta_k + \sgn(y_k)\gamma_k \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \beta_0 = 0 \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-cf58d936c16395b99e7f114581920f3c_l3.png)
Pojawia się jednak problem bo skoro ![]() i
i ![]() jest dowolne to musimy wykonać mnożenie
jest dowolne to musimy wykonać mnożenie ![]() oraz
oraz ![]() . W tym wypadku też jest na to sposób, aby uniknąć tego mnożenia. Mianowicie po prostu o nim zapomnijmy :-). Skutkować to będzie tylko tym, że współrzędna
. W tym wypadku też jest na to sposób, aby uniknąć tego mnożenia. Mianowicie po prostu o nim zapomnijmy :-). Skutkować to będzie tylko tym, że współrzędna ![]() obrazu będzie błędna, a dokładniej to
obrazu będzie błędna, a dokładniej to ![]() . Zwykle przyjmujemy, że
. Zwykle przyjmujemy, że ![]() , ale nie jest to konieczne. Jeśli przyjmiemy
, ale nie jest to konieczne. Jeśli przyjmiemy ![]() , to wtedy będziemy obliczać
, to wtedy będziemy obliczać ![]() .
.
Po ![]() iteracjach odczytujemy znalezioną wartość funkcji
iteracjach odczytujemy znalezioną wartość funkcji ![]()
![Rendered by QuickLaTeX.com \[\arctg \frac{A_y}{A_x} \approx x_n \\\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-c9f9cc76958e435fe109b22a23574fb1_l3.png)
Przykłady trybu wektorowego
Poniżej zwizualizowane i rozpisane są dwa przykłady. Pierwszy dotyczy obliczania ![]() , a drugi obliczenia
, a drugi obliczenia ![]() .
.
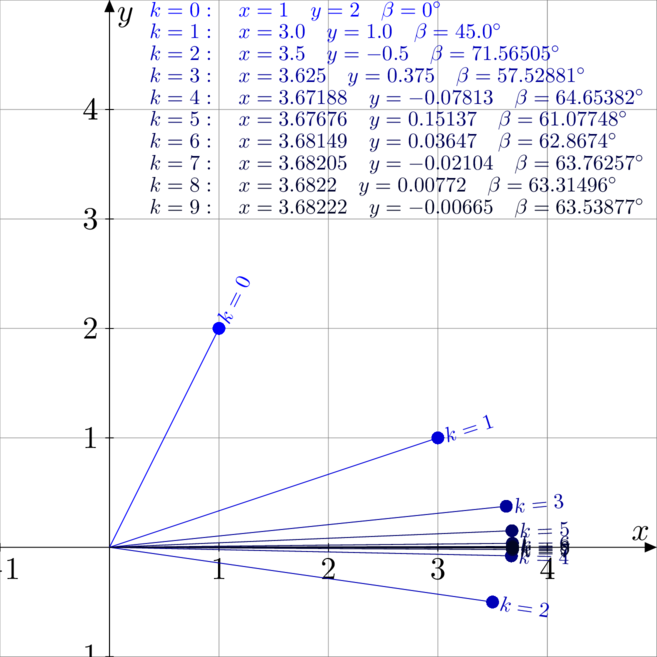
Algorytm obliczania funkcji 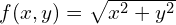
W trybie wektorowym istnieje także możliwość obliczenia pierwiastka kwadratowego. Jest jednak pewne ale, mianowicie nie można tego wykorzystać do obliczenia funkcji ![]() . No chyba, że znamy rozkład
. No chyba, że znamy rozkład ![]() na
na ![]() i
i ![]() postaci
postaci ![]() . Zobaczmy, że nawet, gdyby przyjąć
. Zobaczmy, że nawet, gdyby przyjąć ![]() w funkcji
w funkcji ![]() , to
, to ![]() . Wychodzi na to, że znając
. Wychodzi na to, że znając ![]() możesz policzyć jego wartość bezwzględna, czyli żaden z tego pożytek. Co więcej wymagało by to mnożenia na starcie, bo w tym przypadku nie możemy zignorować mnożenia
możesz policzyć jego wartość bezwzględna, czyli żaden z tego pożytek. Co więcej wymagało by to mnożenia na starcie, bo w tym przypadku nie możemy zignorować mnożenia ![]() . Zignorowanie skutkowało by tym, że końcowy wynik byłby podzielony przez
. Zignorowanie skutkowało by tym, że końcowy wynik byłby podzielony przez ![]() .
.
W przypadku obliczania funkcji ![]() , bez mnożenia się nie obejdziemy. Jeśli mnożenie jest dostępne to wtedy faktycznie możemy obliczać wartości funkcji
, bez mnożenia się nie obejdziemy. Jeśli mnożenie jest dostępne to wtedy faktycznie możemy obliczać wartości funkcji ![]() .
.
Podsumowanie – tryb rotacyjny i tryb wektorowy
Zestawiając ze sobą omówione dwa tryby, po chwili zauważamy, iż zarówno tryb rotacyjny jak i tryb wektorowy możemy zapisać wspólnie.
![Rendered by QuickLaTeX.com \[\begin{tabular}{|c|c|} \hline Tryb rotacyjny & Tryb wektorowy \\ \hline $ \begin{cases} x_{k + 1} = x_{k} - \sgn(\beta_k)y_{k}2^{-k} \\ y_{k + 1} = y_{k} + \sgn(\beta_k)x_{k}2^{-k} \\ \beta_{k + 1} = \beta_{k} - \sgn(\beta_k)\gamma_k \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \beta_0 = \varphi\\ \end{cases} $ & $ \begin{cases} x_{k + 1} = x_{k} + \sgn(y_k) y_{k}2^{-k}\\ y_{k + 1} = y_{k} - \sgn(y_k) x_{k}2^{-k}\\ \beta_{k + 1} = \beta_k + \sgn(y_k)\gamma_k \\ x_{0} = A_x K_{n} \\ y_{0} = A_y K_{n} \\ \beta_0 = 0 \\ \end{cases} $ \\ \hline \end{tabular}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-588197a2db9ce26e708b0869fbd9a869_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x_{k + 1} = x_{k} - d_k y_{k}2^{-k}\\ y_{k + 1} = y_{k} + d_k x_{k}2^{-k}\\ \beta_{k + 1} = \beta_k - d_k \gamma_k \\ \end{cases}\]](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-ade024f79ad84a9df6bf9a5aa1271df4_l3.png)
Tryb rotacyjny
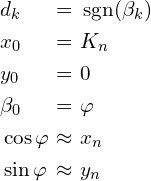
Tryb wektorowy
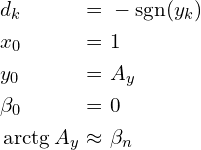
W następnej części omówiony zostanie tryb liniowy. Następna cześć jest dostępna tutaj




