Zbiór punktów, w których wyróżnik równania 4 stopnia jest równy 0

Posted on by Mateusz Kowalski

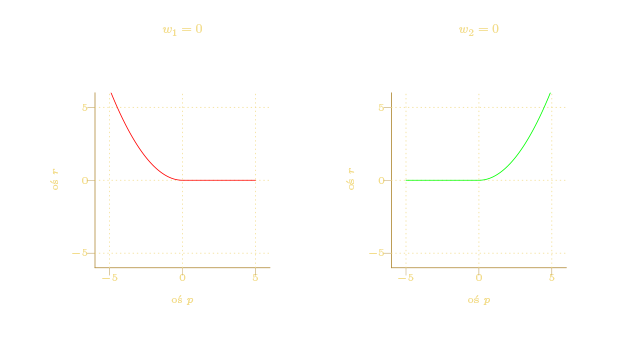
Dla równania postaci

    \[x^4 + px^2 + qx + r =0\]

wyróżnik wyraża się wzorem:

    \[\Delta = 16p^4r - 4p^3q^2 - 128p^2r^2 + 144pq^2r - 27q^4 + 256r^3\]

Tam gdzie wyróżnik jest równy 0 tam równanie wielomianowe ma jakiś (może więcej) wielokrotny (być może zespolony) pierwiastek.

Interesujący jest zatem zbiór punktów \Delta = 0
Zbiór punktów spełniający \Delta = 0 prowadzi do równania

    \[16p^4r - 4p^3q^2 - 128p^2r^2 + 144pq^2r - 27q^4 + 256r^3 = 0\]

W czym problem?

Czasami jak chcemy się dowiedzieć, gdzie funkcja się zeruje, to ją rysujemy i odczytujemy zbiór punktów dla których się zeruje, przykładowo:

    \[f(x) = x^2-3\]

    \[f(x,y) = x^2 - y^3\]

Problem jednak w tym, że na wykres funkcji:
f(x) potrzeba 2 wymiarów
f(x,y) potrzeba 3 wymiarów
\Delta(p,q,r) potrzeba 4 wymiarów

Nawet gdyśmy to narysowali to za wiele nie zobaczmy.
Nas interesuje tylko \Delta=0 więc na taki zbiór punktów wystarczą 3 wymiary

Jak zatem zarysować

    \[16p^4r - 4p^3q^2 - 128p^2r^2 + 144pq^2r - 27q^4 + 256r^3 = 0 ?\]

Dlaczego jest to postać uwikłana, bo nie da się napisać w żadnej z postaci:

p = f(q,r)
q = f(p,r)
r = f(p,q)

Obliczmy wartości wyznacznika dla przykładowych punktów, niech to będzie 11^3 punktów, czyli po 11 na każdy wymiar w zakresie od -5 do 5
dla \Delta > 0 punkt malujemy na czerwono
dla \Delta < 0 punkt malujemy na niebiesko
jak przypadkiem uda nam się wstrzelić idealnie w \Delta = 0 to na zielono



Wydawać by się mogło, że pozostają tylko metody przybliżone, zużywające dużo mocy obliczeniowej.
Czy naprawdę nie da się nic zrobić?
Nasz zbiór punktów, który chcemy narysować nie jest bardzo paskudny. Jest to funkcja nie byle jaka tylko jest to wielomian 3 zmiennych, 5 stopnia.
Różniczkowalna, pochodne też

Spróbujmy się jednak przyjrzeć temu inaczej jakby to wyglądało, gdyby przyjąć, że p jest niewiadomą a q i r są dane

    \[16{\R{p^4}}r - 4{\R{p^3}}q^2 - 128{\R{p^2}}r^2 + 144{\R{p}}q^2r - 27q^4 + 256r^3=0\]

Potem analogicznie gdyby to q było dane, a p i r nie
Następnie gdyby to r było dane a p i q nie

    \[- 27{\R{q^4}} + ( 144pr - 4p^3){\R{q^2}} + 16p^4r - 128p^2r^2 + 256r^3=0\]

    \[256{\R{r^3}} - 128p^2{\R{r^2}} +(144pq^2 + 16p^4 ){\R{r}} - 4p^3q^2 - 27q^4 =0\]

Zacznijmy od pozycji z q

    \[- 27{\R{q^4}} + ( 144pr - 4p^3){\R{q^2}} + 16p^4r - 128p^2r^2 + 256r^3=0\]

Przy okazji już widać, że ten zbiór jakikolwiek jest to na pewno jest symetryczny względem q, innymi słowy płaszczyzna q=0 jest symetrią tego zbioru punktów
Podstawmy za q^2 = w i rozwiążmy równanie ze względu na w

    \[- 27{\R{w^2}} + ( 144pr - 4p^3){\R{w}} + 16p^4r - 128p^2r^2 + 256r^3=0\]

\Delta_2 = 16(p^2 + 12r)^3
w_1 = \frac{8\,p}{3}\,r+\frac{2\sqrt{{\left(p^2+12\,r\right)}^3}}{27}-\frac{2\,p^3}{27}
w_2 = \frac{8\,p}{3}\,r-\frac{2\sqrt{{\left(p^2+12\,r\right)}^3}}{27}-\frac{2\,p^3}{27}
Jeśli któryś dodatni lub równy 0 to pierwiastkujemy i mamy rozwiązania
Dla danego p i r może być 4,3,2,1,0 rozwiązań

Teraz wystarczy powstawiać jakąś matrycę punktów p i r, wyliczyć do nich odpowiednie q i nanieś na wykres
Wszystkie tak wyznaczone punkty rzecz jasna będą punktami ze zbioru \Delta=0
Widać trochę więcej, lecz w dalszym ciągu są to tylko wyizolowane punkty. Nie do końca wiemy jak te punkty połączyć, aby narysować powierzchnie.



Zauważmy pewien wąs rachunek potwierdza, że dla q = 0, to

    \[16p^4r - 128p^2r^2 + 256r^3=0\]

    \[16r = 0 \quad \vee \quad p^4-8p^2r+16r^2 = 0\]

r= 0 \dalej p\in \RR czyli prosta r=0=q
(p^2-4r)^2=0 \dalej r(p) = \frac{p^2}{4}
Zobaczmy, że metodami przybliżonymi najprawdopodobniej byśmy tego nie znaleźli
W pierwszej chwili można się mocno zdziwić, bo …

w_1 = \frac{8\,p}{3}\,r+\frac{2\sqrt{{\left(p^2+12\,r\right)}^3}}{27}-\frac{2\,p^3}{27}
w_2 = \frac{8\,p}{3}\,r-\frac{2\sqrt{{\left(p^2+12\,r\right)}^3}}{27}-\frac{2\,p^3}{27}
w_{1,2} = 0 \dalej 8\cdot 9pr \pm 2\sqrt{(p^2+12r)^3} - 2p^3 = 0
(p^2+12r)^3 = (p^3 - 36pr)^2
p^6 +36rp^4 + 3\cdot 12^2r^2p^2 + 12^3 r^3 = p^6 -72p^4r + 36^2p^2r^2
108rp^4 + (36\cdot 12 - 36^2)p^2r^2 +12^3r^3=0
r=0 \vee 16r^2-8p^2r+p^4 = 0
r=0 \vee (4r-p^2)^2 = 0
r=0 \vee r = \frac{p^2}{4}

w_1(r=0) = \frac{2|p^3|-2p^3}{27} = \begin{cases}0 & \mbox{ dla } p>0\\ \frac{-4p^3}{27} & \mbox{ dla } p<0 \end{cases}
w_2(r=0) = \frac{-2|p^3|-2p^3}{27} = \begin{cases}0 & \mbox{ dla } p<0\\ \frac{-4p^3}{27} & \mbox{ dla } p>0 \end{cases}
w_2(r=\frac{p^2}{4}) = \frac{2p^3}{3} -\frac{2\sqrt{(4p^2)^3}}{27} -\frac{2p^3}{27} = \frac{9p^3 - 8|p^3| - p^3}{27} = \begin{cases}0 & \mbox{ dla } p>0\\ \frac{16p^3}{27} & \mbox{ dla } p<0 \end{cases}
w_1(r=\frac{p^2}{4}) = \frac{2p^3}{3} +\frac{2\sqrt{(4p^2)^3}}{27} -\frac{2p^3}{27} = \frac{9p^3 + 8|p^3| - p^3}{27} = \begin{cases}0 & \mbox{ dla } p<0\\ \frac{16p^3}{27} & \mbox{ dla } p>0 \end{cases}

w1w2=0

\frac{\partial w_1}{\partial r} = \frac{8p}{3} + \frac{2}{27} \frac{3(p^2+12r)^2\cdot 12}{2\sqrt{(p^2+12r)^3}}
\frac{\partial w_1}{\partial r}(r=0) = \frac{8p}{3} + \frac{4}{3}\frac{p^4}{|p^3|} = \frac{8p}{3} +\frac{4}{3} p \sgn (p) = \begin{cases} \frac{12p}{3} & \mbox{ dla } p>0 \\ \frac{4p}{3} & \mbox{ dla } p<0 \end{cases}
\frac{\partial w_1}{\partial r}(r=\frac{p^2}{4}) = \frac{8p}{3} + \frac{4}{3} \cdot \frac{(4p^2)^2}{\sqrt{(4p^2)^3}} = \frac{8p}{3} + \frac{4}{3} \cdot \frac{16p^4}{8|p^3|}=\frac{8p}{3}(1+\sgn(p))= \begin{cases} 0 & \mbox{ dla } p<0 \\ \frac{16p}{3} & \mbox{ dla } p>0 \end{cases}

\frac{\partial^2 w_1 }{\partial r^2} = \frac{\partial}{\partial r} \nawias{ \frac{4}{3} \sqrt{p^2 + 12r} } = \frac{4}{3} \cdot \frac{12}{2\sqrt{p^2+12r}}
\frac{\partial^2 w_1 }{\partial r^2} (r = \frac{p^2}{4}) = \frac{4}{3} \cdot \frac{12}{2\sqrt{4p^2}} = \frac{4}{|p|}>0
Analogicznie z w_2
\frac{\partial w_2 }{\partial r} (r = 0) = \frac{8p-4p\sgn (p)}{3} = \begin{cases} \frac{4p}{3}, & \mbox{ p>0 } \\ 4p, & \mbox{ p<0 } \end{cases} = \begin{cases} >0, & \mbox{ p>0 } \\ <0, & \mbox{ p<0 } \end{cases}
\frac{\partial w_2 }{\partial r} (r = \frac{p^2}{4}) = \begin{cases} 0 &\mbox{ dla } p>0 \\ \frac{16p}{3} & \mbox{ dla } p<0 \end{cases}
\frac{\partial^2 w_1}{\partial r^2}(r=\frac{p^2}{4}) = \frac{-4}{|p|}<0





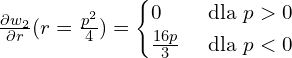
Popatrzmy na to od strony r
256{\R{r^3}} - 128p^2{\R{r^2}} +(144pq^2 + 16p^4 ){\R{r}} - 4p^3q^2 - 27q^4 =0
Wprawdzie jest tutaj trudniej, to jednak stopień jest mniejszy, wiec cały zbiór będzie składać się maksymalnie z 3 powierzchni.
Przekształcamy do równanie do postaci kanonicznej \tilde{r} = r - \frac{p^2}{6}
\tilde{r}^3 + \tilde{p}\tilde{r}+\tilde{q}=0






    \[256{\R{r^3}} - 128p^2{\R{r^2}} +(144pq^2 + 16p^4 ){\R{r}} - 4p^3q^2 - 27q^4 =0\]

    \[\tilde{r}^3 + \tilde{p}\tilde{r}+\tilde{q}=0\]

    \[\tilde{r} = r - \frac{p^2}{6}\]

    \[\tilde{p} = \frac{-p(p^3 - 27q^2)}{48}\]

    \[\tilde{q} = \frac{p^6}{864} + \frac{5p^3q^2}{64} - \frac{27q^4}{256}\]

    \[\tilde{\Delta}_3=\tilde{q}^2 + \frac{4\tilde{p}^3}{27} = \frac{q^2(8p^3 + 27q^2)^3}{1769472}\]

    \[\tilde{\Delta}_3 =0 \dalej p(q) = -\frac{3}{2}\sqrt[3]{q^2}\]

    \[\tilde{\Delta}_3 >0 \dalej p(q) > -\frac{3}{2}\sqrt[3]{q^2}\]

Dzięki temu mamy wzory na odpowiednie powierzchnie

Jedna powierzchnia dla \tilde{\Delta}_3 > 0
Trzy powierzchnie dla \tilde{\Delta}_3 < 0
Wąs gdy q=0

    \[r = \sqrt[3]{\frac{\sqrt{3(q^2(8p^3 + 27q^2)^3)}}{4608} - \frac{p^6}{1728} +\frac{27q^4}{512} - \frac{5p^3q^2}{128}} +\]

    \[+ \sqrt[3]{\frac{-\sqrt{3(q^2(8p^3 + 27q^2)^3)}}{4608} - \frac{p^6}{1728} +\frac{27q^4}{512} - \frac{5p^3q^2}{128}} +\frac{p^2}{6}\]

3 powierzchnie

    \[\varphi = \arccos \nawias{ \frac{-8p^6 - 540p^3q^2 + 729q^4}{8\nawias{\sqrt{p^4 - 27q^2p}}^3} }\]

    \[r_1 = \frac{1}{6}\sqrt{p^4 - 27q^2p}\cdot \cos\frac{\varphi}{3} + \frac{p^2}{6}\]

    \[r_2 = \frac{1}{6}\sqrt{p^4 - 27q^2p}\cdot \cos\frac{\varphi+2\pi}{3} + \frac{p^2}{6}\]

    \[r_3 = \frac{1}{6}\sqrt{p^4 - 27q^2p}\cdot \cos\frac{\varphi+4\pi}{3} + \frac{p^2}{6}\]


Be Sociable, Share!

Comments

comments

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.