Złota proporcją interesowali się już starożytni można ja znaleźć w: starożytnych budowlach, w przyrodzie, długości odpowiednich paliczków są w złotej proporcji. Kartka do drukarki (A4) ma długości krawędzi w złotym stosunku.
Złota proporcja jest definiowana następująco. Masz odcinek o pewnej długości i chcesz go tak podzielić, aby długość całego odcinka w stosunku do dłuższej części po podziale miał się tak, jak dłuższa cześć do krótszej części. Długości odcinków muszą spełniać następujące równanie:
Dla takich oznaczeń otrzymujesz następujące równanie:

Gdybyś rozwiązał to równanie to otrzymał byś, że ten stosunek wynosi 1,618033988750
A dokładniej to
Rozwiązanie
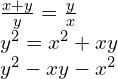
Teraz np. zakładasz, że niewiadomą jest y (rozwiązujemy równanie względem y) i obliczasz wyróżnik trójmianu kwadratowego (deltę).

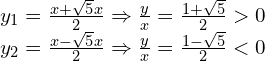 .
. Odcinek
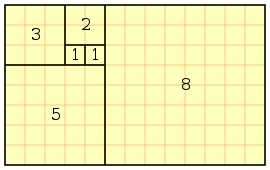
Złota proporcja ma ścisły związek z ciągiem Fibonacciego
Jest to taki ciąg, w którym wartość danego elementu jest równa sumie dwóch poprzednich.
ciąg przyjmuje wartości
Stosunek danego wyrazu do poprzedniego jest w przybliżeniu w złotej proporcji. Przy czym to przybliżenie dąży idealnie do złotej proporcji im wyraz jest większy tym lepsze to przybliżenie.

![]()
![]()
Złota proporcja podobno występuje w przyrodzie, czyli także w zwierzętach w ciele ludzkim. Mówię podobno bo osobiście tego nie sprawdzałem 🙂
poniżej fotki jest tego przeogromna ilość.
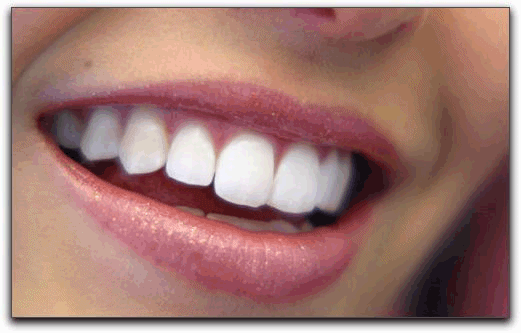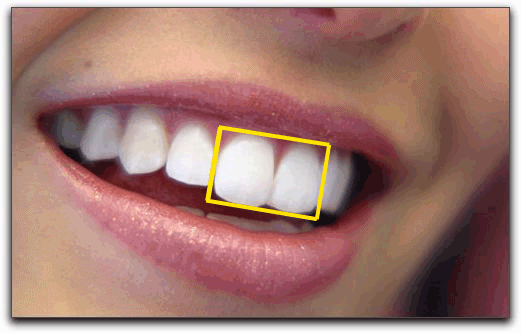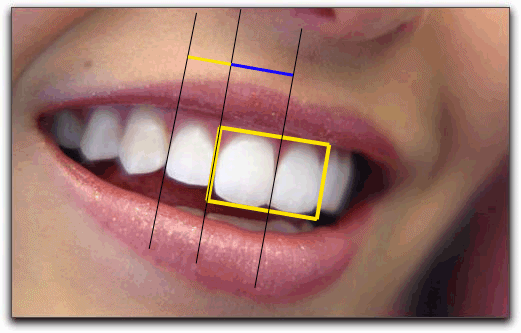

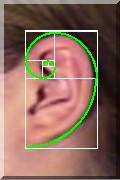








a tu piękny filmik czułem, że coś jest w tych słonecznikach.









kartka do drukarki (A4) –> 297/210=1,414
\frac{odcinek}{dlusza \ czesc}=\frac{dlusza \ czesc}{krutsza \ czesc} -> wybacz ale prócz matematyki trzeba napisać “dłuższa” oraz “krótsza”, więc użyć nieco J.Polskiego