Twierdzenie o 3 ciągach lub funkcjach

Posted on by Mateusz Kowalski

Cóż to takiego. Brzmi co najmniej dziwnie. Jest to naprawdę bardzo proste twierdzenie tak proste, że aż się możesz zdziwić co w nim takiego odkrywczego.
A zatem do dzieła.

Mam bardzo dobry przykład obrazujący to twierdzenie. Wyobraź sobie dwóch policjantów i siebie. Teraz zobacz jak jeden z tych policjantów idzie na posterunek. Potem zwróć uwagę, że drugi policjant także idzie na posterunek. No a ty znajdujesz się cały czas między nimi i także sobie maszerujesz. Wniosek jest taki, że jeśli jesteś cały czas między dwoma policjantami i oni obaj zmierzają do posterunku to Ty także trafisz na posterunek.
Oto całe twierdzenie.

Twierdzenie o 3 ciągach

No dobrze ale do czego jest mi potrzebna taka oczywistość?

Już spieszę z odpowiedzią.
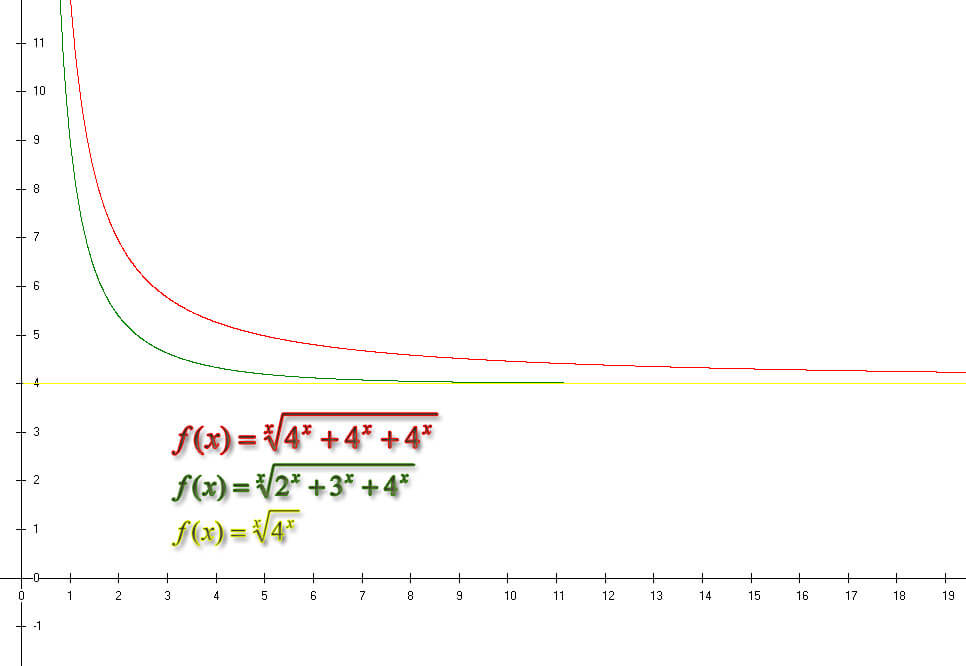
jak policzyć granicę tego ciągu

\lim\limits_{n\to\infty}\sqrt[n]{2^n+3^n+4^n}= \?

Możemy ograniczyć ciągiem większym i mniejszym

\sqrt[n]{4^n}\leqslant \sqrt[n]{2^n+3^n+4^n} \leqslant \sqrt[n]{4^n+4^n+4^n}

obliczając granicę jednego ciągu mamy

\lim\limits_{n\to\infty}\sqrt[n]{4^n}=4

Ale obliczając granicę drugiego ciągu mamy

\lim\limits_{n\to\infty}\sqrt[n]{4^n+4^n+4^n}=\lim_{n\to\infty}\sqrt[n]{3}\cdot\sqrt[n]{4^n}=1\cdot4=4

A zatem granica naszego szukanego ciągu wynosi

\lim\limits_{n\to\infty}\sqrt[n]{2^n+3^n+4^n}=4

Na mocy twierdzenia o 3 ciągach.
Twierdzenie o 3 ciągach

Be Sociable, Share!

Comments

comments

3 thoughts on “Twierdzenie o 3 ciągach lub funkcjach”

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany.