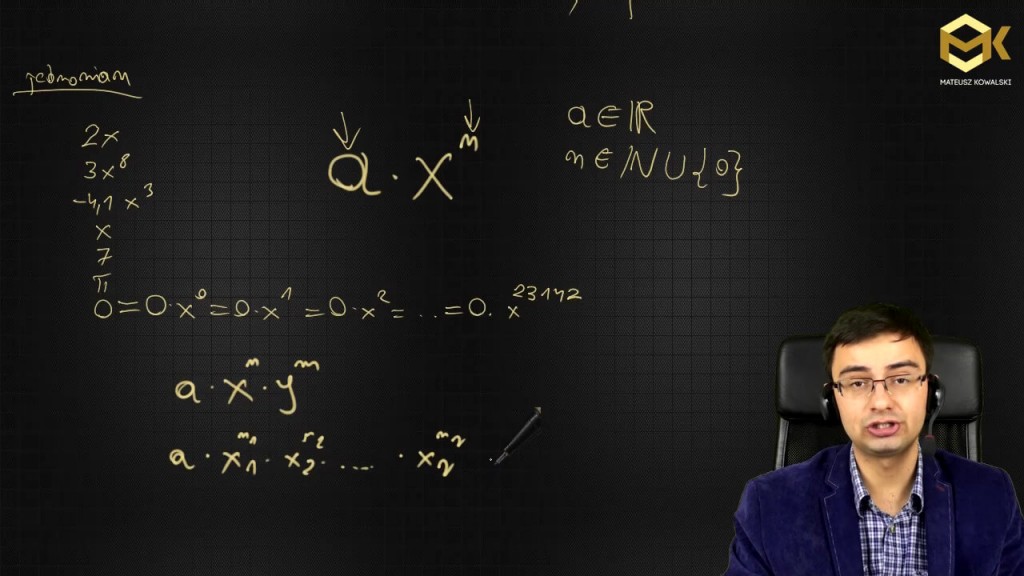Wyrażenie algebraiczne to pewna konfiguracja stałych i zmiennych połączonych przez działania takie jak dodawanie, odejmowanie, mnożenie, dzielenie, ale również potęgowanie i pierwiastkowanie.
![]()
Do tego dochodzą jeszcze nawiasy pozwalające na zmianę kolejności działań. Co ważne to, aby to wyrażenie miało sens i było skończone.
Przykłady
![]()
Nie musi to być jedna zmienna, może ich być więcej
![]()
Jak równie dobrze może ich wcale nie być
![]()
Dla kontrastu przykłady, które nie są wyrażeniami algebraicznymi.
![]()
Jednomian to wyrażenie algebraiczne pewnej szczególnej postaci, dokładniej to takiej.
![]()
gdzie ![]() jest konkretną daną stałą liczbą.
jest konkretną daną stałą liczbą. ![]() . Natomiast to czym jest
. Natomiast to czym jest ![]() zależy już od konkretnego kontekstu.
zależy już od konkretnego kontekstu.
![]() nazywamy współczynnikiem jednomianu
nazywamy współczynnikiem jednomianu
![]() nazywamy stopniem jednomianu
nazywamy stopniem jednomianu
![]() zmienną jednomianu
zmienną jednomianu
Oczywiście jednomian może mieć więcej niż jedną zmienną. Dla dwóch zmiennych będzie to wyglądać tak:
![]()
Stopnie jednomianu jest wówczas suma wykładników przy zmiennych, czyli ![]()
Zmiennych może być jeszcze więcej, jak tu:
![]()
Stopniem takiego jednomianu będzie suma ![]()