Zacznijmy od najprostszego.
Równanie pierwszego stopnia (liniowe)
gdzie
Filozofii to tu nie ma
Równanie drugiego stopnia (kwadratowe)
gdzie
są dwa rozwiązania
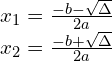
gdzie
Równanie trzeciego stopnia (sześcienne)
tu nie będzie już tak łatwo
gdzie
Najpierw podzielmy przez ![]() , aby mieć
, aby mieć ![]() przy najwyższej potędze niewiadomej.
przy najwyższej potędze niewiadomej.
Zauważmy, iż równanie można sprowadza się do równania postaci, w której nie ma składnika z niewiadomą w kwadracie
łącząc i grupując ze względu na potęgi
gdzie:
Mamy teraz do rozpatrzenia prostsze równanie 3 stopnia w postaci kanonicznej, z niewiadomą ![]() .
.
Nikt nie zabronić tej niewiadomej przedstawić w postaci sumy dwóch innych niewiadomych wielkości.
Wówczas
Przekształcając równanie mamy
Równanie to ma taką samą postać jak nasze wejściowe kanoniczne, czyli
Można zatem utożsamić te równania ze sobą, a co za tym idzie wielkości
Po co to robimy, bo ![]() i
i ![]() jest znane, ponieważ są zdeterminowane przez
jest znane, ponieważ są zdeterminowane przez ![]() , które znamy. Natomiast kombinacja
, które znamy. Natomiast kombinacja ![]() i
i ![]() to jest nasza niewiadomą, którą chcemy znaleźć, więc naszym celem jest “tylko” wyrazić
to jest nasza niewiadomą, którą chcemy znaleźć, więc naszym celem jest “tylko” wyrazić ![]() i
i ![]() od tych znanych wielkości.
od tych znanych wielkości.
Co sprowadza się do układu równań.
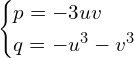
Z pierwszego równania mamy 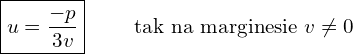
Wstawiamy do drugiego równania. ![]()
Mnożąc obustronnie przez ![]()
![]() mamy równianie trikwadratowe, które sprowadzamy do równania kwadratowego poprzez podstawienie
mamy równianie trikwadratowe, które sprowadzamy do równania kwadratowego poprzez podstawienie![]() Przez to, że
Przez to, że ![]() jest nieznane to teraz nową nieznaną jest
jest nieznane to teraz nową nieznaną jest ![]()
Zagadnienie sprawdziliśmy do równania kwadratowego postaci
Teraz bardzo ważne z delty będziemy liczyć pierwiastek, więc musimy
Skoro znamy
TERAZ UWAGA
Mamy niewiadomą w 3 potędze która jest równa liczbie rzeczywistej. Mamy więc 1 rozwiązanie rzeczywiste i 2 zespolone. Z pierwszym nie ma problemu, bo wystarczy tylko
Przypominamy, że jeśli mamy równanie ![]() to
to
gdzie
![]()
choć wiele osób tak uczy to jest to jawne nadużycie. Czym wówczas były by 3 różne jednostki urojone w kwaternionach, gdzie każda jest inna, oraz kwadrat każdej daje ![]() . Zostawmy to, jednak bo to inny temat i wróćmy do zadania.
. Zostawmy to, jednak bo to inny temat i wróćmy do zadania.
Warto przy tym zdać sobie sprawę z
![]()
![]()
![]() oraz
oraz
![]() jaki i
jaki i
![]()
Takie to ciekawe liczby, choć nie rzeczywiste to bardzo przydatne.
Wykorzystujac ten fakt łatwo rozwiąząć np. ![]()
![]()
![]()
![]()
![]()
Kończąc dygresję, u nas będzie.
![]()
![]()
![]()
Gdy znamy ![]() to wracamy do
to wracamy do ![]() . Wyznaczyliśmy wcześniej, że
. Wyznaczyliśmy wcześniej, że 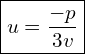
Zobaczmy ile wynosi ![]()
![Rendered by QuickLaTeX.com \frac{1}{v_1} = \sqrt[3]{\frac{-2}{q\R{\mp} \sqrt{\Delta}}}=\sqrt[3]{\frac{-2(q\pm \sqrt{\Delta})}{q^2-\Delta}}= \sqrt[3]{\frac{q\pm \sqrt{\Delta}}{2 \frac{p^3}{3^3}}}=\frac{3}{p}\sqrt[3]{\frac{-q\R{\mp} \sqrt{\Delta}}{2}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-a9fb080d45947c9a90eada60d0e53698_l3.png)
Wymiemy ile teraz wynosi ![]()
![]()
![]()
![]()
![]()
Puki co wydawać by się mogło że mamy 6 potencialnych rozwiązań bo jeszcze dowolność znaku ![]() . Jednak okazuje się, że rozwiązań może być co najwyżej 3, bo
. Jednak okazuje się, że rozwiązań może być co najwyżej 3, bo
![]()
oznacza
![]()
lub
![]()
a to jest to samo.
Mamy zatem końcowe wzory dla przypadku ![]()
————————————————————————–
![]()
![]()
![]()
————————————————————————–
Warto się jeszcze zastanowić Czy ![]() i
i ![]() mogą być kiedyś rzeczywiste okazuje się, że jest to możliwe tylko, gdy
mogą być kiedyś rzeczywiste okazuje się, że jest to możliwe tylko, gdy ![]() i wówczas
i wówczas ![]() i będzie to podwójny rzeczywisty pierwiastek, i innej opcji nie ma.
i będzie to podwójny rzeczywisty pierwiastek, i innej opcji nie ma.
Spójrzmy na ![]()
![]()
Aby cześć urojona się wyzerował to
![]() ,
,
a to jest możliwe tylko gdy ![]()
Analogicznie dla
![]()
wówczas
![Rendered by QuickLaTeX.com \boxed{ y_0 = 2\sqrt[3]{-\frac{q}{2}}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-3dc08c0b58315bcd86559c26ade95af1_l3.png)
![Rendered by QuickLaTeX.com \boxed{y_1=y_2 = -\sqrt[3]{-\frac{q}{2}}}](https://www.kowalskimateusz.pl/wp-content/ql-cache/quicklatex.com-dfe70a705a2a572fb3c914027b86f7b8_l3.png)
Jeśli
Przejdźmy do sytuacji, gdy ![]() . Tutaj sprawa wygląda nieco inaczej.
. Tutaj sprawa wygląda nieco inaczej.
Pierwszy wniosek na marginesie ![]()
Chcąc spierwiastkować liczbę ujemną musimy jej zmienić znak, aby była teraz dodatnia i można było ja spierwiastkować, a tę zmianę korygujemy przemnażając wynik przez ![]() , wówczas:
, wówczas:
![]()
Teraz mamy do spierwiastkowania ![]() liczbę zespoloną, a nie rzeczywistą, więc “trick” z pierwiastkami z jedynki nie zadziała.
liczbę zespoloną, a nie rzeczywistą, więc “trick” z pierwiastkami z jedynki nie zadziała.
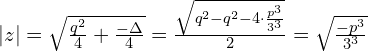
![]()
![]()
![]()
ponieważ ![]() bo
bo ![]()
![]()
dodając ![]() i
i ![]() powstają końcowe wzory.
powstają końcowe wzory.
Warto spostrzec że znak kąta ![]() nie ma znaczenia dla kosinusa, więc można pominąć
nie ma znaczenia dla kosinusa, więc można pominąć ![]() , ponieważ
, ponieważ ![]() , czyli w naszym przypadku
, czyli w naszym przypadku
![]() jaki i
jaki i
![]()
Mamy zatem końcowe wzory dla przypadku ![]()
————————————————————
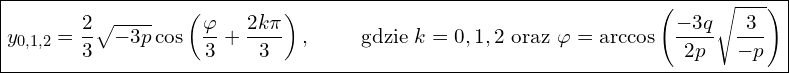
————————————————————-
Zauważ, że w tym wypadku wszystkie 3 rozwiązania są rzeczywiste![]()
Warto przekonać się, iż rozwiązaniem równania
jest
PODSUMOWANIE ALGORYTM DLA KOMPUTERA ROZWIĄZANIA OGÓLNEGO RÓWNANIA O WSPÓŁCZYNNIKACH RZECZYWISTYCH
Aby rozwiązać
Obliczmy
![]()
![]()
![]()
if ![]() to
to
![]()
else if ![]() UWAGA NA DOKŁADNOŚĆ KOMPUTEROWYCH OBLICZEŃ PORÓWNANIA Warto dla
UWAGA NA DOKŁADNOŚĆ KOMPUTEROWYCH OBLICZEŃ PORÓWNANIA Warto dla ![]() lepiej badać
lepiej badać ![]() , które jest przemnożeniem delty przez
, które jest przemnożeniem delty przez ![]() i korzystamy tu ze źródłowych danych
i korzystamy tu ze źródłowych danych ![]()
![]()
![]()
else if![]() to
to
![]() słaby ze względu na nie dokładności numeryczne, może powodować dla kątów bliskich
słaby ze względu na nie dokładności numeryczne, może powodować dla kątów bliskich ![]() i
i ![]() , czyli gdy
, czyli gdy ![]() zwielokrotnienie błędu niedokładności.
zwielokrotnienie błędu niedokładności.
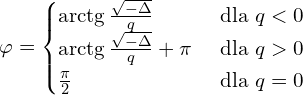
Uwaga na ![]() bliskie zeru, wówczas lepiej użyć wzoru szarego na
bliskie zeru, wówczas lepiej użyć wzoru szarego na ![]() . Ponadto jeśli
. Ponadto jeśli ![]() i
i ![]() są bliskie
są bliskie ![]() , a to ma miejsce przy dużym
, a to ma miejsce przy dużym ![]() to wówczas lepiej wzoru, bazującego na źródłowych danych
to wówczas lepiej wzoru, bazującego na źródłowych danych ![]() czyli po przekształceniu
czyli po przekształceniu ![]()
![]()
end
![]()
Równanie czwartego stopnia
Tu będzie jeszcze trudniej, ale jeszcze można.
gdzie
Zamieniajmy niewiadomą
Skorzystajmy ze wzoru skróconego mnożenia.
Zróbmy rachunki pomocnicze
Podstawiamy do równania i uprośćmy
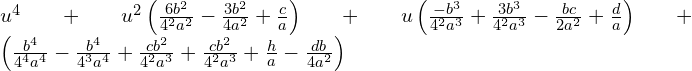
Dodając z lewej i prawej strony równania ![]()
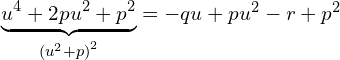
Teraz dodając z lewej i prawej strony pewną niewiadomą wartość ![]() , a dokładniej
, a dokładniej ![]()
![]()
![]()
Z lewej strony równania mam kwadrat to z prawej też musi być kwadrat, aby równianie było prawdziwe. Skoro tak to z prawej strony musi być ![]() , czyli podwójny pierwiastek, więc
, czyli podwójny pierwiastek, więc ![]() równania kwadratowego
równania kwadratowego ![]() ze względu na
ze względu na ![]() , (bo
, (bo ![]() jest niewiadomą), po prawej stronie musi być równa
jest niewiadomą), po prawej stronie musi być równa ![]()
![]()
czyli ![]()
Chcąc znaleźć niewiadomą
Po znalezieniu rozwiązań, których liczba to 1, 2 lub 3, znamy wartość ![]()
![]()
ponieważ trójmian kwadratowy z deltą równą 0 można zapisać tak ![]()
Przekształcając i odejmując obustronie prawą stronę otrzymamy
![]()
Mamy tutaj różnicę dwóch kwadratów ![]() , czyli
, czyli
![]()
Teraz aby znaleźć ![]() , bo
, bo ![]() już znamy trzeba rozwiązać równie kwadratowe.
już znamy trzeba rozwiązać równie kwadratowe.
![]()
![]()
W związku z tym, że znak dodania lub odjęcia ![]() nie jest zależy od wyboru pozostałych znaków, to dla porządku oznaczyłem go przez
nie jest zależy od wyboru pozostałych znaków, to dla porządku oznaczyłem go przez ![]()
Wydawać by się mogło, że mamy zatem aż 2 razy 2 razy 3 czyli 12 kandydatów na rozwiązanie ogólnego równania 4 stopnia. Natomiast w ogólnej sytuacji mamy 8 możliwych opcji.
1) brak rozwiązań
2) 1 rozwiązanie podwójne
3) 2 rozwiązania pojedyncze
4) 2 rozwiązania podwójne
5) 2 rozwiązania pojedyncze i 1 podwójne
6) 1 rozwiązanie pojedyncze i 1 potrójne
7) 4 pojedyncze
8) 1 rozwiązanie poczwórne
Choć ze względu na liczbę pierwiastków licząc także krotność to mamy albo 0 pierwiastków albo 2 albo 4.
Równanie piątego stopnia i wyższych
gdzie
“Problem rozwiązalności takich równań badany był od końca XVI wieku, gdy matematycy włoscy podali wzory na rozwiązania równań stopni 3 i 4. Zmagali się z nim Bézout, Euler i Lagrange, jednak dopiero Paolo Ruffini wpadł na pomysł, by udowodnić, że w przypadku równań stopnia wyższego niż 4 odpowiednie wzory nie istnieją. Opublikowany przez niego w roku 1799 dowód twierdzenia (Ruffini podał pięć dowodów) zawierał pewne nieścisłości i został zignorowany przez społeczność matematyków – być może przyczyną był fakt, że Ruffini był także lekarzem. W pełni zadowalający dowód opublikował w roku 1824 Niels Henrik Abel, został on następnie uproszczony w roku 1845 przez Pierre’a Wantzela. Jednak znacznie głębsza analiza problemu zawarta jest w pracach Évariste’a Galois pod postacią teorii Galois.” źródło Wikipedia
źródła:
Matematyka.pl
Wikipedia









W równaniu kwadratowym jest byk, bo napisał Pan sqrt{delta}=b^2-4ac, a powinno być delta=b^2-4ac. Ale poza tym bardzo fajne metody.
Nie mniej jednak ja znam krótsze. Wystarczy ustalić, przez jaki dwumian liniowy można podzielić wielomian, a następnie wykonywać to tyle razy, aż dojdziemy do trójmianu kwadratowego.
faktycznie błąd poprawiony. Nie zawsze można łatwo znaleść ten dwumian liniowy. Np wielomian 4 stopnia może składać się z 2 trójmianów nie rozkładalnych i wtedy nie jest łatwo to rozpisać.
Wiem 😀 Jak to pisałem, to w ogóle nie czaiłem równań stopnia >2. To ja jestem tym wielbiącym Pana dwunastolatkiem, który wygrał kurs całek 🙂
Proszę sprawdzić alfa1 i alfa2 przecież są różne.Fajne opracowanie
Fajnie opisany sposób jak rozwiązywać takie równania, jednak tak na moje oko jest błąd w “delcie” ze względu na “u” przy rozwiązywaniu równań 4 stopnia. Nie będę pisał poprawnego rozwiązania bo jest na wikipedii (wzór nr. 18), które sprawdziłem i się z nim zgadzam.
Szkoda, że nie rozpisał Pan tego do końca, albo algorytmem tak jak w równaniu 3-go stopnia, ponieważ gubię się co mam zrobić po wyznaczeniu trzech wyników v1, v2 i v3. Między innymi nie jest dla mnie zrozumiałe skąd bierze się to +-
“Zmagali się z nim Bézout, Euler i Lagrange, jednak dopiero Paolo Ruffini wpadł na pomysł, by udowodnić, że w przypadku równań stopnia wyższego niż 4 odpowiednie wzory nie istnieją”
Może by tak w gwoli ścisłości powiedzieć, że w tezach tych dowodów jest to że dane wzory muszą być zrobione za pomocą już znanych funkcji rzeczywistych.
Według mnie podejście to jest dosyć naiwne, w kontekście tego jak tworzono znane nam wzory. Wystarczy sobie przypomnieć jakim szokiem dla starożytnych było odkrycie funkcji pierwiastka kwadratowego. Warto zauważyć że każde kolejne algorytmy na rozwiązywanie równań liniowych kolejnych stopni rozszerzało definicje funkcji rzeczywistych. W takim kontekście przewidywanie że równania 5 stopnia mają być “robione” starymi metodami bez nowej funkcji rzeczywistej jest dosyć szokujące. Rozumiem żeby zrobić to tak dla sprawdzenia “czy da się po staremu” i później próbować zasadniczych metod to i owszem, ale jeśli później pomniejsi matematycy piszą o tym tak : “tak się zupełnie nie da, nie idźcie dalej tą bezowocną drogą” to już jest niezła herezja. Pisząc konkretniej jeśli sprowadzimy równanie 5 stopnia do funkcji 3 zmiennych to wtedy mamy krzywą ciągłą zależną od jednego parametru a i prostą bx +c. Krzywa 5 stopnia jednej zmiennej ma określone przedziały wklęsłości i wypukłości które można ściśle wyznaczyć w zależności od tego parametru. Przyrównując pochodną krzywej i prostą możemy dla ustalonych parametrów a i b, odszukać wartość c dla której prosta jest styczna do krzywej (max 4). Idąc dalej tą drogą wyznaczymy, dla ustalonych a i b przedziały parametru c w których prosta przecina krzywą konkretną ilość razy, co da nam wyróżniki badanego równania 5 stopnia. Skoro zaś mamy przedziały w których prosta i krzywa się przecinają oraz wiemy w jaki sposób, to da się prosto stworzyć funkcje(od 3 zmiennych) która przy odpowiednich przyrostach a, b i c szybko będzie wyznaczać duże przybliżenia. Oczywiście tradycyjnie można ją nazwać rzeczywistą (bo czemu nie). I tak oto mamy tradycyjne wyróżniki oraz wzory na równanie 5 stopnia oraz klarowną sytuacje do dalszych rozważań, czyli wszystko co naprawdę było potrzebne.