Wektory i wartości własne (Eigenvalues and eigenvectors)

Nim zaczniemy Powinneś zadać jedno mądre pytanie.

1. Do czego to jest potrzebne i gdzie się tego używa?
Na dobrą sprawę w życiu każdego studenta/studentki kierunków ścisłych przychodzi moment kiedy słyszy o wektorach własnych i wartościach własnych. Ja osobiście usłyszałem o wektorach własnych i wartościach własnych na wielu przedmiotach.
Między innymi na: algebrze i analizie liniowej, podstawach automatyki, procesach losowych i sterowaniu stochastycznym, identyfikacji procesów, nowoczesnych metodach teorii sterowania, sterowaniu cyfrowym, równaniach różniczkowych, geometrii różniczkowej.

Na sterowaniu świat się nie kończy. Założę się, że na innych kierunkach techniczny na pewno także się to wykorzystuje, przykłady: W celu diagonalizacji macierzy, by potem móc np. łatwo potęgować macierz, do pierwiastkowania macierzowego albo podnoszenie e do potęgi macierzowej. W PCA, które zaś jest używa np. do kompresji sygnałów. W algorytmie ICA, czyli przy rozkładaniu mieszani na sygnały oryginalne. W fizyce i chemii kwantowej. W badaniu stabilności układów dynamicznych. Google wykorzystuje przy ocenianiu strony – page rank (ranking stron).
I wiele wiele innych nie sposób tu tego wymienić. Także naprawdę jest to bardzo ważne i użyteczne.

2. Co robi odwzorowanie dane macierzą?
Powiedzmy, że mamy wektor $\mathbf{v}=\left[ \begin{matrix} {{v}_{x}} \\ {{v}_{y}} \\ \end{matrix} \right]=\left[ \begin{matrix} 1 \\ 2 \\ \end{matrix} \right]$

i chcemy go przekształcić przez odwzorowanie dane macierzą

$\mathbf{A} =\left[ \begin{matrix} 1 & 0 \\ 0 & 2 \\ \end{matrix} \right]$
to co powstanie?
$\mathbf{w} = \mathbf{A} \cdot \mathbf{v}$
Obliczmy
$\mathbf{w}=\left[ \begin{matrix} 1 & 0 \\ 0 & 2 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} 1 \\ 2 \\ \end{matrix} \right]=\left[ \begin{matrix} 1\cdot 1+0\cdot 2 \\ 0\cdot 1+2\cdot 2 \\ \end{matrix} \right]=\left[ \begin{matrix} 1 \\ 4 \\ \end{matrix} \right]$
Co się stało? W wyniku tego odwzorowania wektor się 2 wydłużył w kierunku y.

Weźmy inną macierz np.

$\mathbf{A} =\left[ \begin{matrix} 0 & -1 \\ 1 & 0 \\ \end{matrix} \right]$
W wyniku tego przekształcenia uzyskamy
$\mathbf{w}=\left[ \begin{matrix} 0 & -1 \\ 1 & 0 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} 1 \\ 2 \\ \end{matrix} \right]=\left[ \begin{matrix} -2 \\ 1 \\ \end{matrix} \right]$
Co się tym razem stało?
W wynik tego odwzorowania wektor się obrócił o 90 stopni.

Jeszcze inny

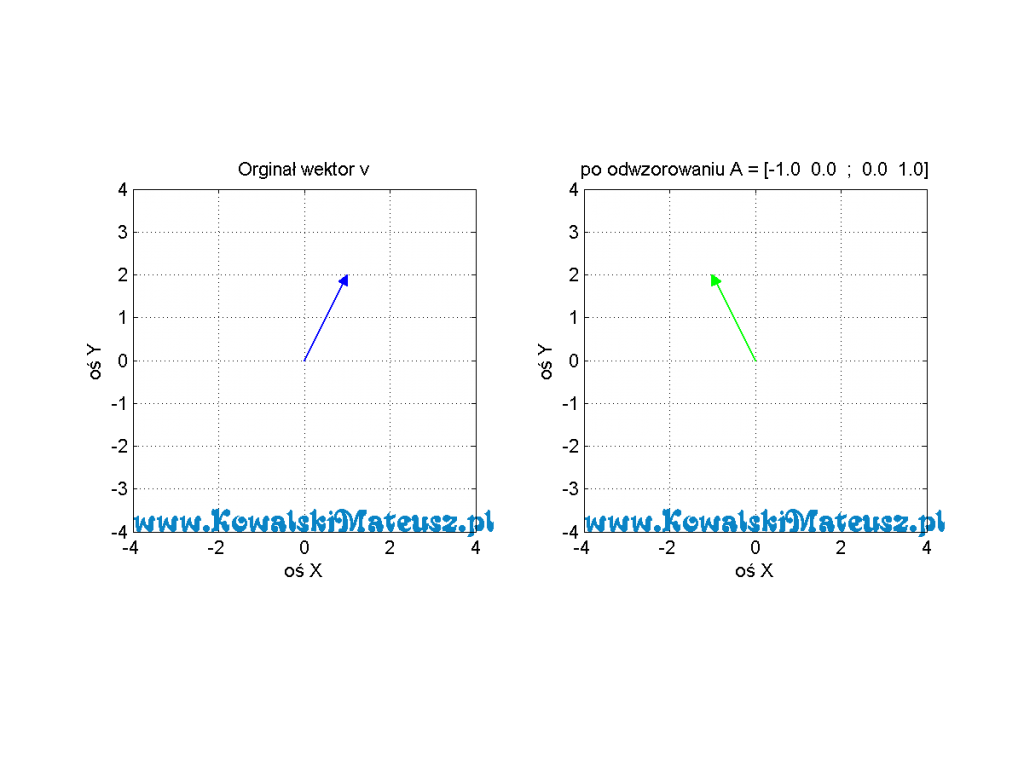
$\mathbf{A} =\left[ \begin{matrix} -1 & 0 \\ 0 & 1 \\ \end{matrix} \right]$
uzyskany wektor to
$\mathbf{w}=\left[ \begin{matrix} -1 & 0 \\ 0 & 1 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} 1 \\ 2 \\ \end{matrix} \right]=\left[ \begin{matrix} -1 \\ 2 \\ \end{matrix} \right]$
Tym razem to wektor “odbił się lustrzenia”.

________________________________________________________________
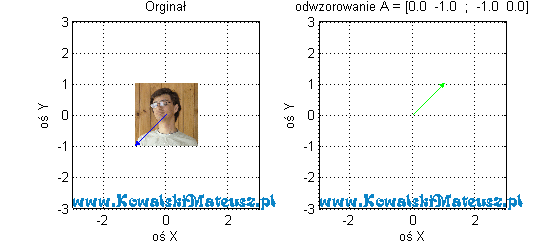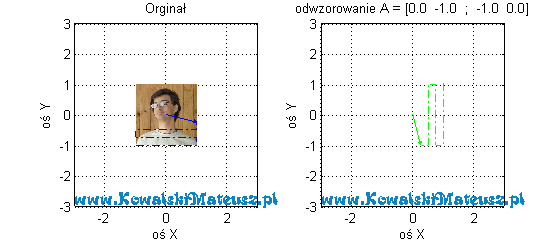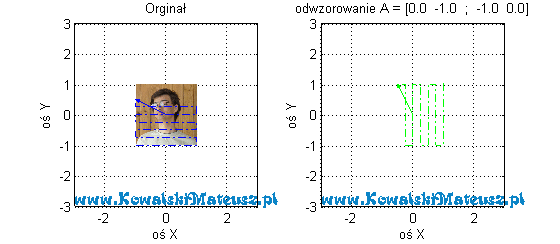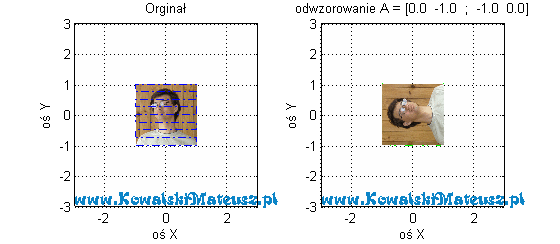
Przekształcając jeden wektor nie widać za bardzo “zachowania” danego odwzorowania. Dając jakiś wektor dostajemy inny. Spójrz co się będzie działo, gdy całą rodzinę różnych wektorów przekształcimy przez dane odwzorowanie. Można powiedzieć, że przekształcamy ogólny wektor $\mathbf{v}=\left[ \begin{matrix} {{v}_{x}} \\ {{v}_{y}} \\ \end{matrix} \right]$ , a nie jakiś szczególny.
Rozpatrzmy odwzorowaniem dane wzorem

$\mathbf{A} =\left[ \begin{matrix} 1 & 0 \\ 0 & 2 \\ \end{matrix} \right]$

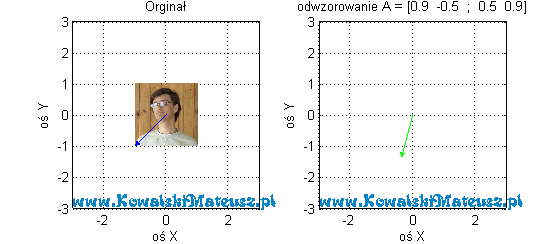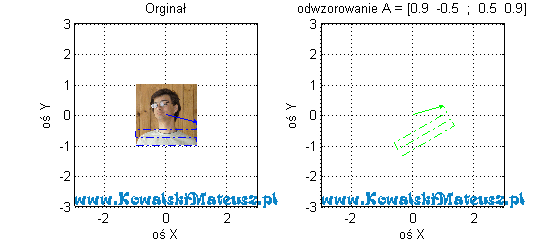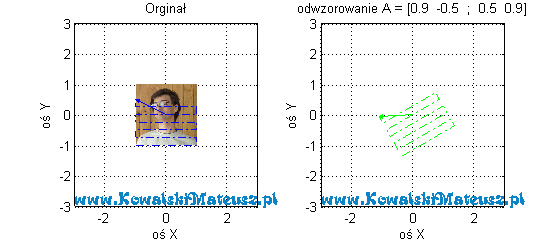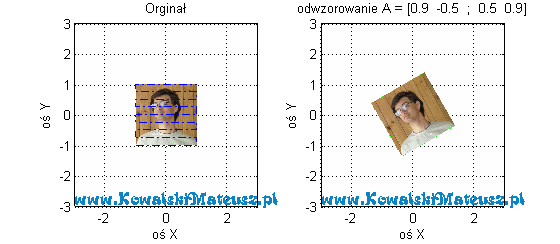
I co teraz obserwujemy? Każdy niebieski wektor po odwzorowaniu ma składową y 2-krotnie większą.
Dołożyłem tu jeszcze zdjęcie, aby lepiej było widać ten efekt odwzorowania.

Dla odwzorowania danego macierzą.

$\mathbf{A} =\left[ \begin{matrix} 0 & -1 \\ 1 & 0 \\ \end{matrix} \right]$

I co teraz obserwujemy? Obrót o $+90^{\circ}$
Kolejne z poprzednich odwzorowań.

$\mathbf{A} =\left[ \begin{matrix} -1 & 0 \\ 0 & 1 \\ \end{matrix} \right]$

Tu obserwujemy “lustrzane odbicie”

Dlaczego wektor Jest zaczepiony w (0,0)? Bo chciałem utożsamić go ze współrzędnymi punktu na płaszczyźnie.

________________________________________________________________
Rozpatrzyliśmy 3 główne przekształcenia możliwe przez macierz. Jak się pewnie domyślasz te przekształcenia można analogicznie wykonać dla drugiej współrzędnej.
Oczywiście istnieją kombinacje tych przekształceń. Jak się zapewne domyślasz kolejność przekształceń ma znaczenie. Co innego to zrobić lustrzaną symetrię, a potem obrót, niż obrót a potem lustrzaną symetrię. Przykład poniżej.

a) w pierwszym przypadku

$\mathbf{w} =\left[ \begin{matrix} 0 & 1 \\ -1 & 0 \\ \end{matrix} \right] \cdot \left( \left[ \begin{matrix} -1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \cdot \left[ \begin{matrix} v_x \\ v_y \\ \end{matrix} \right] \right)$
nawias jest zbędny jest tylko w celach dydaktycznych

$\mathbf{A} =\left[ \begin{matrix} 0 & 1 \\ -1 & 0 \\ \end{matrix} \right] \cdot \left[ \begin{matrix} -1 & 0 \\ 0 & 1 \\ \end{matrix} \right] = \left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]$
Czyli wykonujemy tutaj najpierw symetrię względem prostej osi y (lustrzane odbicie), a potem dokonujemy obrotu o kąt $-90^{\circ}$ , efekt poniżej.

$\mathbf{A} =\left[ \begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix} \right]$

b) w odwrotnej kolejności

$\mathbf{w} =\left[ \begin{matrix} -1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \cdot \left( \left[ \begin{matrix} 0 & 1 \\ -1 & 0 \\ \end{matrix} \right] \cdot \left[ \begin{matrix} v_x \\ v_y \\ \end{matrix} \right] \right)$
nawias jest zbędny jest tylko w celach dydaktycznych

$\mathbf{A} =\left[ \begin{matrix} -1 & 0 \\ 0 & 1 \\ \end{matrix} \right] \cdot \left[ \begin{matrix} 0 & 1 \\ -1 & 0 \\ \end{matrix} \right] = \left[ \begin{matrix} 0 & -1 \\ -1 & 0 \\ \end{matrix} \right]$
Tu najpierw obrót o $-90^{\circ}$ , a potem symetrię względem prostej osi y, poniżej efekt.

$\mathbf{A} =\left[ \begin{matrix} 0 & -1 \\ -1 & 0 \\ \end{matrix} \right]$

Zwracam twoją uwagę na to, że mnożenie macierz w ogólności nie jest przemienne, tzn. $\mathbf{A} \cdot \mathbf{B} \neq \mathbf{B} \cdot \mathbf{A}$ . Co znalazło swoje odzwierciedlenie w tym przykładzie.
________________________________________________________________
Inne odwzorowania obejrzyj.

W ogólności macierz obrotu o dany kąt $\alpha$ wyraża się wzorem:

$\mathbf{A}=\left[ \begin{matrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{matrix} \right]$
obrót o 30 stopni

$\mathbf{A} =\left[ \begin{matrix} 1 & 2 \\ 2 & 1 \\ \end{matrix} \right]$

Tak na marginesie zauważ, iż każde odwzorowanie dane macierzą liczb jest liniowe i ciągłe. A Co to znaczy, że jest liniowe i ciągłe?

Liniowe oznacza, że zniekształcenie ma “charakter liniowy”. Podam przykład jednego zniekształcenia nieliniowego.

a tu masz przekształcenie (odwzorowanie) nieciągłe.

Mamy dobre wprowadzenie, przejdźmy zatem do rzeczy.

3. Wektory własne, wartości własne i kierunki własne.
Zastanów się czy dla danego odwzorowania, które jest macierzą. $\mathbf{A}$ może być taki wektor, który po przekształceniu będzie taki sam, mimo że w ogólności dla danego odwzorowania tak nie jest. Jaki by wówczas był warunek?

Przekształcamy wektor $\mathbf{v}$ , no i mamy nowy wektor $\mathbf{w}$ , czyli $\mathbf{w}=\mathbf{Av}$ . Ponadto chcemy, aby ten wektor był taki sam $\mathbf{w}=\mathbf{v}$ albo ewentualnie przeskalowany $\mathbf{w}=\lambda \mathbf{v}$ . $\lambda}$ jest pewną stała liczbą. Możemy zatem nasz warunek wyrazić przez $\mathbf{Av} = \lambda \mathbf{v}$ .

Nim rozwiążemy ten problem zobrazujmy o co chodzi. Na potrzebę zobraowania weźmy sobie $\mathbf{A}=\left[\begin{matrix} 1 & 0,5 \\ 0 & 2 \end{matrix} \right]$ oraz $\mathbf{v}=\left[ \begin{matrix} 1 \\ 2\end{matrix} \right]$ przykładu

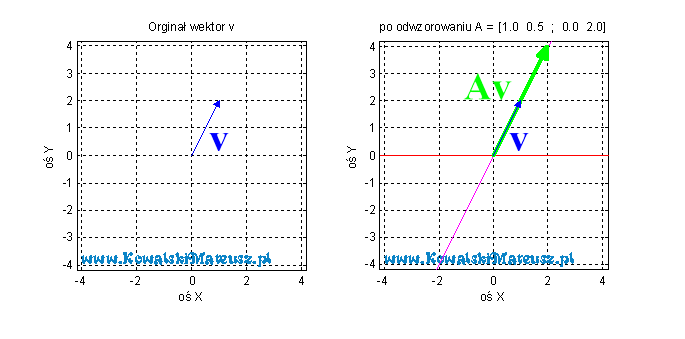
Wektor, który po przeskalowaniu wskazuje ten sam kierunek jest wektorem własnym. Jest to taki szczególny wektor odwzorowania $\mathbf{A}$ , który jest “odporny” na odwzorowanie. Macierz $\mathbf{A}$ tylko co najwyżej skaluje (zmniejsza, zwiększa, ewentualnie zmienia zwrot).

Jak to skalowanie wygląda?

$\lambda$ -razy powiększa w kierunku $x$ i $y$ . Albo jak kto woli $\lambda$ -razy zwiększa długość (jak $0<\lambda<1$ to będzie zmniejszał, a jak $\lambda>1$ to zwiększał), a jak $\lambda<0$ to będzie zmieniał zwrot. Oczywiście jak $\lambda <-1$ to będzie powiększał i obracał.

Stała $\lambda$ , która odpowiednio skaluje nazywana jest wartością własną. Każda wartość własna ma przypisany odpowiedni wektor własny $\mathbf{v}$ .

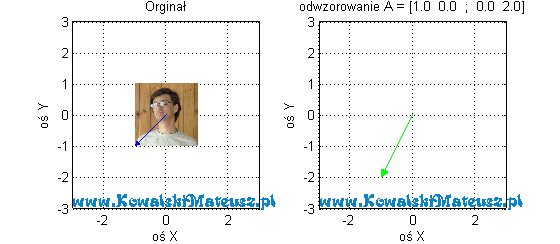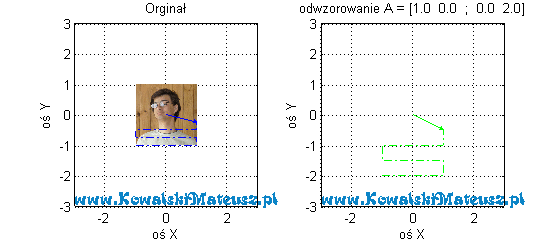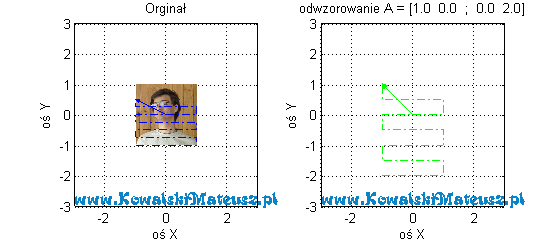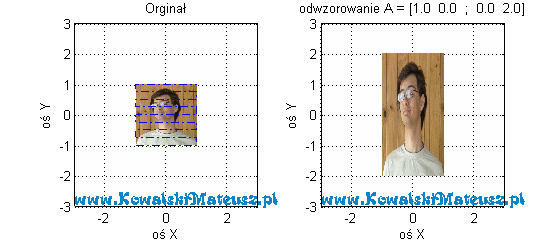
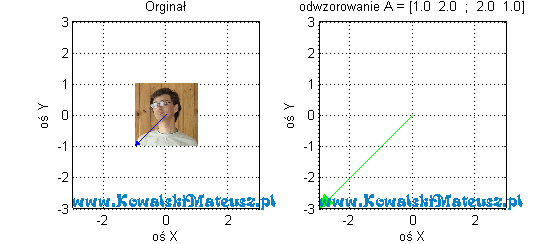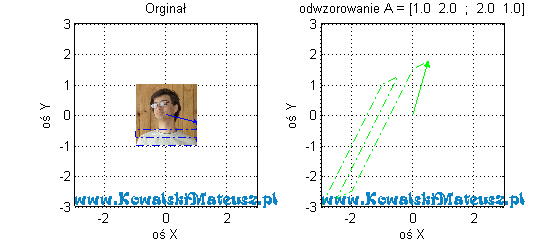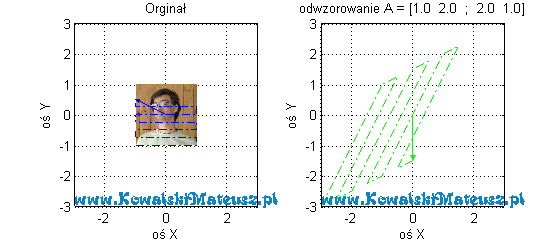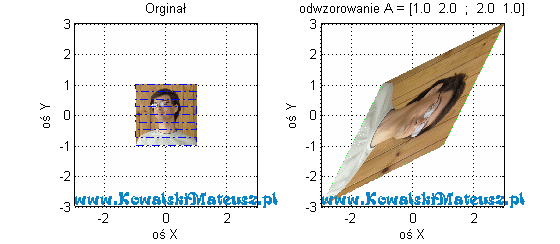
Zobaczmy jak to odwzorowanie wygląda na zdjęciu

$\mathbf{A} =\left[ \begin{matrix} 1 & 0,5 \\ 0 & 2 \\ \end{matrix} \right]$

________________________________________________________________
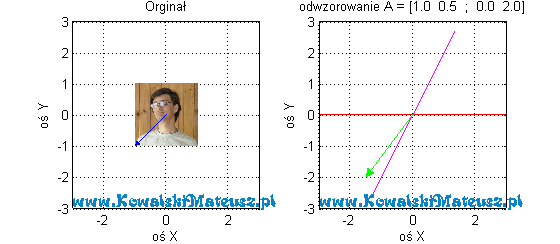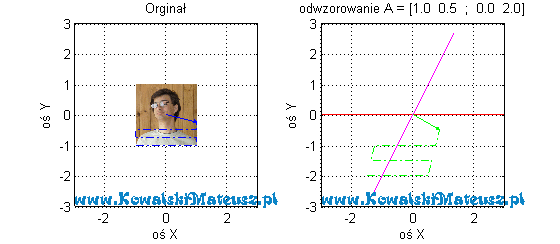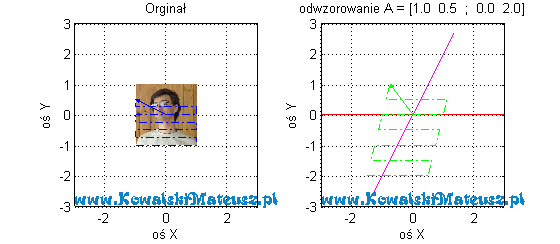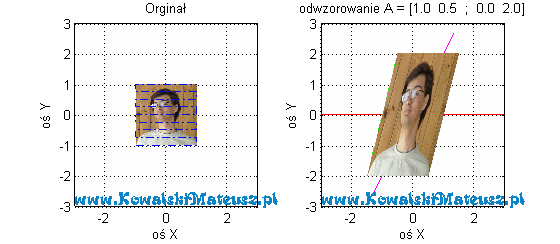
Rozwiążmy postawiony problem.
$\mathbf{Av} = \lambda \mathbf{v}$ tu należy dodać, iż wektor zerowy nas nie interesuje, gdyż taki zawsze by spełnił nasze równanie nie było by w nim niczego szczególnego, zatem $\mathbf{v} \neq \mathbf{0}$ .

Krok 1. przenosimy na drugą stronę bo nam wolno

$\mathbf{Av}-\lambda \mathbf{v}=\mathbf{0}$

Krok 2. wyłączamy za nawias wektor $\mathbf{v}$

$\mathbf{(A-I\lambda )v}=\mathbf{0}$

Krok 3. teraz najważniejsze, stwierdzamy że musi być tak:

$\det \mathbf{(A-I\lambda )}=0$
dlaczego? No właśnie kiedyś to dla mnie też było nie jasne. Wyjaśnijmy to.

Mamy równanie

$\mathbf{(A-I\lambda )v}=\mathbf{0}$
są dwie możliwości

$\det \mathbf{(A-I\lambda )}\neq 0$ albo
$\det \mathbf{(A-I\lambda )} = 0$
Jakby nie patrzeć jest to prawda albo się równa zero albo nie, innej możliwości nie ma.
Zajmijmy się najpierw przypadkiem

$\det \mathbf{(A-I\lambda )}\neq 0$ .
Jeśli tak by było to wynika z tego, że istnieje

$\mathbf{(A-I\lambda )}^{-1}$ ,
bo wyznacznik jest nie zerowy. Okej no w takim razie mogę sobie to równanie
$\mathbf{(A-I\lambda )v}=\mathbf{0}$
przemnożyć lewostronnie przez $\mathbf{(A-I\lambda )}^{-1}$ dostaję
$\mathbf{(A-I\lambda )}^{-1}\mathbf{(A-I\lambda )v}=\mathbf{(A-I\lambda )}^{-1}\cdot \mathbf{0}$ upraszczając

$\mathbf{Iv}}=\mathbf{0}$
$\mathbf{v}}=\mathbf{0}$

Jedyne rozwiązanie jakie uzyskaliśmy to $\mathbf{v}}=\mathbf{0}$ , a przecież założyliśmy, że takie rozwiązanie nas nie interesuję.

Pozostała 2 możliwość.

$\det \mathbf{(A-I\lambda) }=0$
W wielu książkach następuje od razu przeskok
$\mathbf{(A-I\lambda )v}=\mathbf{0}$
$\det \mathbf{(A-I\lambda) }=0$

Krok 4.
W tym równaniu $\lambda$ jest niewiadomą, bo $\mathbf{A}$ jest przecież dane bo dla danej macierzy szukamy wartości własnych i wektorów własnych.
pytanie jest zatem $\lambda=?$ obliczając ten wyznacznik uzyskamy jakiś wielomian stopnia takiego jakiego rozmiaru jest macierz $\mathbf{A}$ . czyli:

$\det \mathbf{(A-I\lambda)}=\left|\begin{array}{ccc}a_{11}-\lambda &\ldots & a_{1n}\\ \vdots & \ddots & \vdots \\a_{n1}&\ldots &a_{nn}-\lambda \end{array}\right|=c_n\cdot \lambda^n+\ldots c_1\cdot \lambda + c_0 = f(\lambda)$
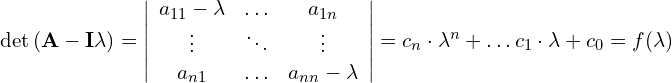
Wyznacznik równa się $0$ , więc problem sprowadza się do rozwiązania równania wielomianowego $n$ -tego stopnia, tzn.
$c_n\cdot \lambda^n+\ldots c_1\cdot \lambda + c_0 = 0$
Zatem z równania znajdujemy $n$ -różnych $\lambda$ , które są wartościami własnymi. A gdzie są wektory własne?.

Krok 5. Znajdujemy wektory własne
Wracając do równania:

$\mathbf{(A-I\lambda )v}=\mathbf{0}$ Wystarczy podstawić kolejne wartości własne $\lambda_i$ i znajdować dla nich kolejne odpowiadające im wektory własne $\mathbf{v_i}$ .

PRZYKŁAD
Weźmy sobie dla przykładu taką macierz

$\mathbf{A} =\left[ \begin{matrix} 1 & 0,5 \\ 0 & 2 \\ \end{matrix} \right]$
rozwiązanie
$\det \mathbf{(A-I\lambda )}=\left| \begin{array}{cc} 1-\lambda & 0,5\\0 &2-\lambda \end{array} \right| = (1-\lambda)\cdot (2-\lambda)-0=\lambda^2-3\lambda +2$
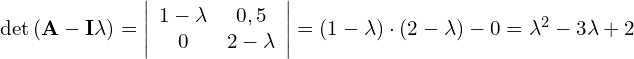
wiemy, że ten wyznacznik musi być równy 0 (pokazywaliśmy dlaczego), stąd.
$\lambda^2-3\lambda +2=0$
$\lambda_1 = \frac{3-1}{2}=1$
$\lambda_2 = \frac{3+1}{2}=2$
Okej mamy wartości własne teraz szukamy wektorów własnych odpowiadających danym wartoscią własnym.
Dla $\lambda_1=1$ mamy $\mathbf{A-\lambda_{1} \cdot I}=\mathbf{0}$
$\left[ \begin{matrix}1-1 & 0,5 \\ 0 & 2-1 \end{matrix} \right] \cdot \left[ \begin{matrix} v_1 \\ v_2 \end{matrix} \right] = \left[ \begin{matrix} 0 \\ 0 \end{matrix} \right]$
czyli mamy układ równań:
$\begin{cases} 0\cdot v_1+0,5 \cdot v_2 =0 \\0\cdot v_1+1 \cdot v_2 =0 \end{cases}$
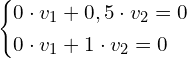
czyli $v_1 \in R$ , a $v_2 = 0$ W ten sposób uzyskaliśmy, że dowolny wektor leżący (równoległy) do osi $x$ jest wektorem własnym dla wartości własnej $\lambda_1=1$ np. $\mathbf{v}=\left[ \begin{matrix} 1 \\ 0 \end{matrix} \right]$

Wyznaczmy teraz dla drugiej wartości własnej.
Dla $\lambda_2=2$ mamy $\mathbf{A-\lambda_{2} \cdot I}=\mathbf{0}$

$\left[ \begin{matrix}1-2 & 0,5 \\ 0 & 2-2 \end{matrix} \right] \cdot \left[ \begin{matrix} v_1 \\ v_2 \end{matrix} \right] = \left[ \begin{matrix} 0 \\ 0 \end{matrix} \right]$
czyli mamy układ równań:
$\begin{cases} -1\cdot v_1+0,5 \cdot v_2 =0 \\0\cdot v_1+0 \cdot v_2 =0 \end{cases}$
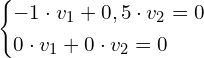
czyli $v_2 = 2v_1$ . Czyli W ten spsób uzyskaliśmy, że dowolny wektor leżący (równoległy) do prostej $y=2\cdot x$ jest wektorem własnym dla wartości własnej $\lambda_2=2$ np. $\mathbf{v}=\left[ \begin{matrix} 1 \\ 2 \end{matrix} \right]$

Prosta, która jest równoległa do danego wektora własnego jest kierunkiem własnym macierzy. Na ostatnich rysunkach są one zaznaczone jako czerwona i różowa prosta. Uproszczając na razie to macierz stopnia 2 ma dwie rożne wartości własne i dwa odpowiadające im wektory własne. Tak naprawdę to wektorów własnych jest nieskończenie wiele, ale są tylko dwa z dokładnością do skalowania tych wektorów (dwie proste).

Zauważmy, że jak szukamy wektora własnego to tak naprawdę znajdujemy kierunek własny, a to jaki wybierzemy wektor własny, jest obojętne byle był równoległy do kierunku własnego.

Nie sądziłem, że ten post wyjdzie taki dułgi, a i tak dopiero ruszyłem czubek góry lodowej.

Ten sam artykuł w wersji nagrania wideo.

Be Sociable, Share!

Comments

comments

19 thoughts on “Wektory i wartości własne (Eigenvalues and eigenvectors)”

l

9 lutego 2013 at 14:14

Świetny artykuł! Wreszcie można zrozumieć do czego to de facto służy. Gratuluję!

Odpowiedz
mi

5 marca 2013 at 08:10

Witam
Dla mnie też artykuł jest świetny. Gdybyś mógł to dodaj generator plików .pdf żbye można było dołączyć go do notatek.

Odpowiedz
Mateusz Kowalski

5 marca 2013 at 15:35

Miło mi, że się podoba, jednak kodów nie udostępnię.

Odpowiedz
TNT

30 marca 2013 at 12:59

Dzięki Mateusz za tak dokładne wytłumaczenie, bo już miałem rezygnować z samodzielnej nauki teorii sterowania.

Odpowiedz
Mateusz Kowalski

2 kwietnia 2013 at 22:26

Bardzo mi miło, że ten materiał Ci pomógł.

Odpowiedz
Anonim

13 października 2013 at 17:43

Dokładnie tego szukałam:)!

Odpowiedz
Anonim

3 stycznia 2014 at 18:05

Bardzo dziękuję za przystępne wytłumaczenie spotykanych zagadnień! Świetnie połączyłeś teorię z praktyką, a dzięki ilustrowanym przykładom zawiłe, odległe zagadnienia stają się w pełni zrozumiałe! DZIĘKUJĘ!

Odpowiedz
Anonim

21 czerwca 2014 at 18:44

Dziękuję za ten wykład!

Odpowiedz
Pingback: 25 Czym Są Wartości Własne i Wektory Własny | KowalskiMateusz.pl
Paulina

10 lipca 2015 at 12:15

Mógłbyś zwrócić uwagę na poprawność językową, literówki, stylistykę. Pozdrawiam serdecznie

Odpowiedz
Bartosz Jenner

17 września 2015 at 17:59

Brawo!
Moja praca polega na stosowaniu metod statystycznych w planowaniu i analizie danych z badan klinicznych. Jednak kierunek jaki skonczylem to biologia – czyli na codzien stosuje algorytmy ktorych podstaw matematycznych nie rozumiem (ale o tym cicho sza). Ten artykul pozwolil mi zrozumiec dlaczego techniki wielowymiarowej analizy danych typu PCA (Principal Component Analysis) moga “dzialac”. Bardzo mi sie tez podoba rozumienie macierzy jako “sposobu dzialania na wektor(y)”. Ogromne dzieki.
Bartek

Odpowiedz
- Mateusz Kowalski
  
  17 września 2015 at 18:21
  
  Miło mi, że mogłem pomóc i dziękuję Ci bardzo za komentarz.
  
  Odpowiedz
  - monia
    
    16 czerwca 2017 at 23:42
    
    eee to jest super, nigdy mi nikt tego tak nie wytłumaczył, rewelacja, wielkie dzięki
    
    Odpowiedz
Mikołaj Kuziuk

6 marca 2016 at 08:04

Obejrzałem ten artykuł w wersji wideo, jest dosyć ciekawy. Ja też tak mam, że siadam, chcąc napisać krótki dokument, a wychodzi – diabli wiedzą jak długi 😀

Odpowiedz
Radosław Matusik

4 listopada 2016 at 11:25

Nie ma w języku polskim słowa “orginał”…

Odpowiedz
Student

29 grudnia 2016 at 22:00

Super, cieszę się że akurat ta strona mi się wyświetliła, będę odwiedzał częściej !!! Pozdrawiam serdecznie, i dziękuję za cudowny artykuł

Odpowiedz
Magda

17 maja 2017 at 20:22

Dobra robota! Wielkie dzięki 🙂

Odpowiedz
Ania

18 maja 2017 at 08:28

Jest Pan Mistrzem, bo tylko Mistrz nie boi się dzielić swoją wiedzą. Bardzo dobrze wytłumaczone, pięknie.

Odpowiedz
- Mateusz Kowalski
  
  18 maja 2017 at 12:39
  
  Dziękuję Bardzo. Polecam jeszcze materiał “hardcore’owy” Rozkład Jordana Macierzy
  
  Odpowiedz

Twoje Internetowe Wsparcie Matematyczne

Wektory i wartości własne (Eigenvalues and eigenvectors)

Comments

19 thoughts on “Wektory i wartości własne (Eigenvalues and eigenvectors)”

Dodaj komentarz Anuluj pisanie odpowiedzi

Imię:		*
Email:		*