Weźmy sobie jakąś krzywą zamkniętą, powiedzmy taką jak na rysunku obok. Następnie wybierzmy jakiś punktu, niech to będzie ![]()
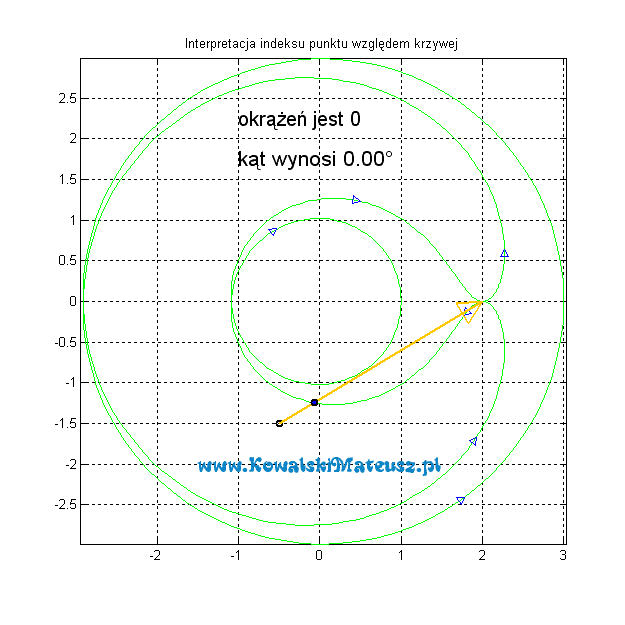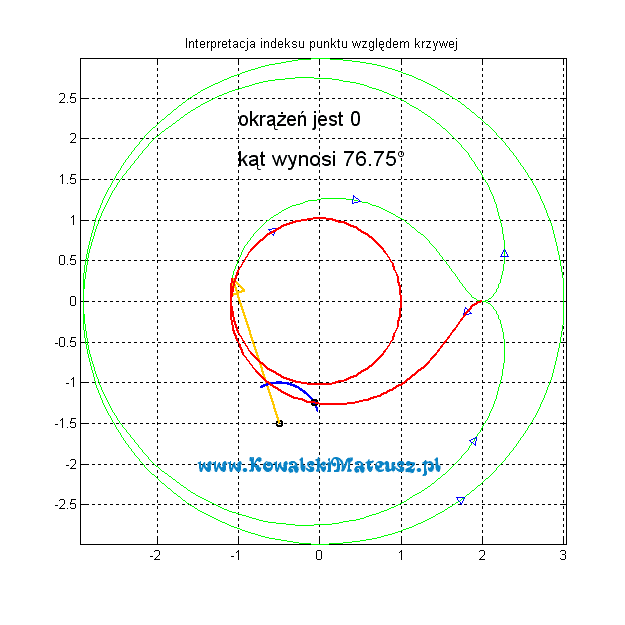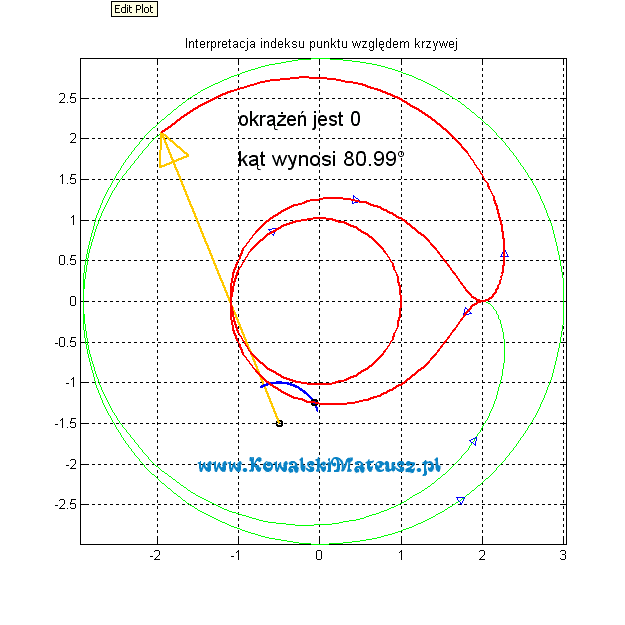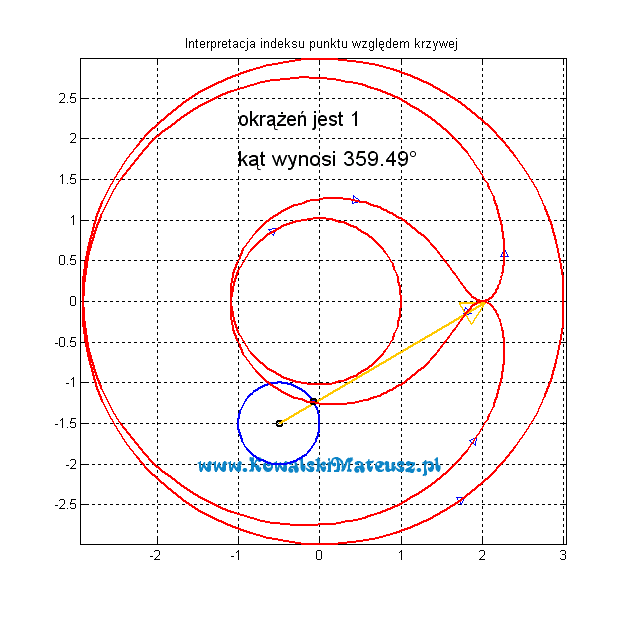
Postarajmy się obiec tą krzywą, ale patrząc z punktu widzenia tego wybranego punktu i sprawdźmy ile razy musimy się obrócić, aby ją obejrzeć. Żółta strzałka to miejsce, na które patrzymy. Poniżej przedstawiona jest animacja interpretując graficznie problem.
Kiedy podczas oglądania krzywej obrócimy się w prawo wówczas należy doliczyć 1 natomiast, kiedy odpowiednio obrócimy się w lewo wtedy należy odjąć 1.
Suma pełnych okrążeń w prawo minus suma pełnych okrążeń w lewo daje pewną liczbę w przykładzie powyżej jest to -2 (zero obrotów w prawo i 2 obroty w lewo). Tą liczbę nazywamy indeksem punktu względem krzywej. W naszym przykładzie zapisuje się to tak ![]()
Jest twierdzenie, które głosi, iż indeks punktu względem krzywej jest liczbą całkowitą dla krzywej zamkniętej.
Poniżej animacje dla indeksów innych punktu, względem tej samej krzywej.
Przy okazji tego przykładu możesz zobaczyć wykresy zmiany kąta w trakcie obiegania oraz długości wektora na poniższym zdjęciu.
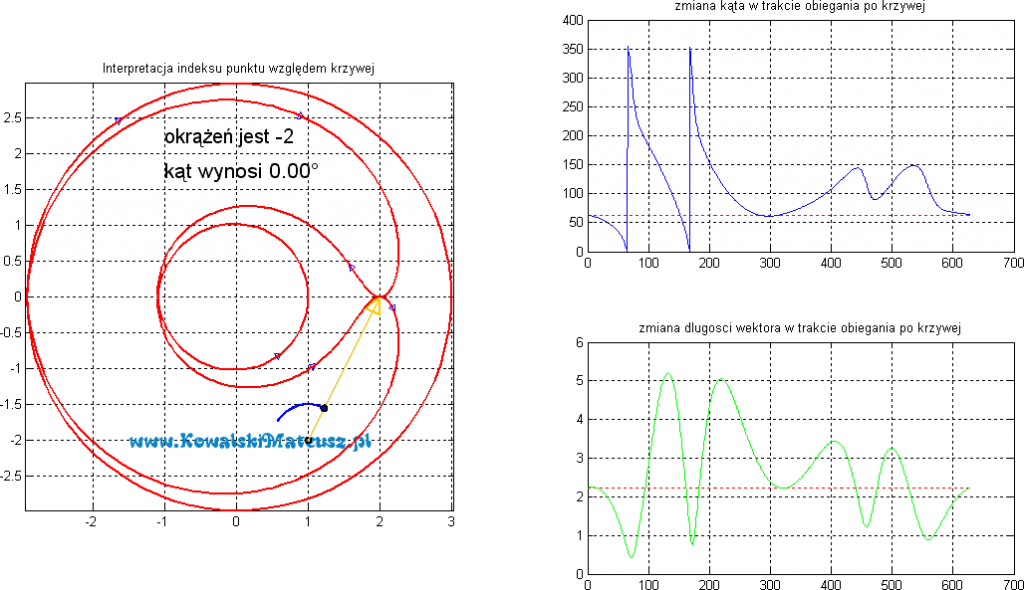
kolejny przykład
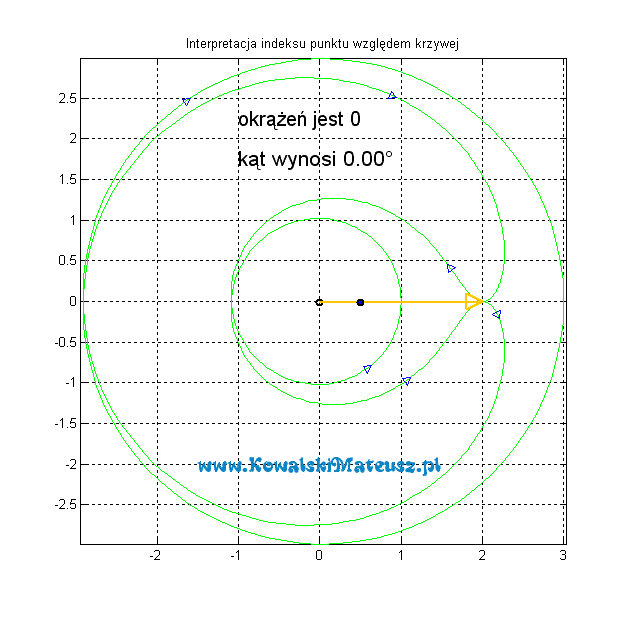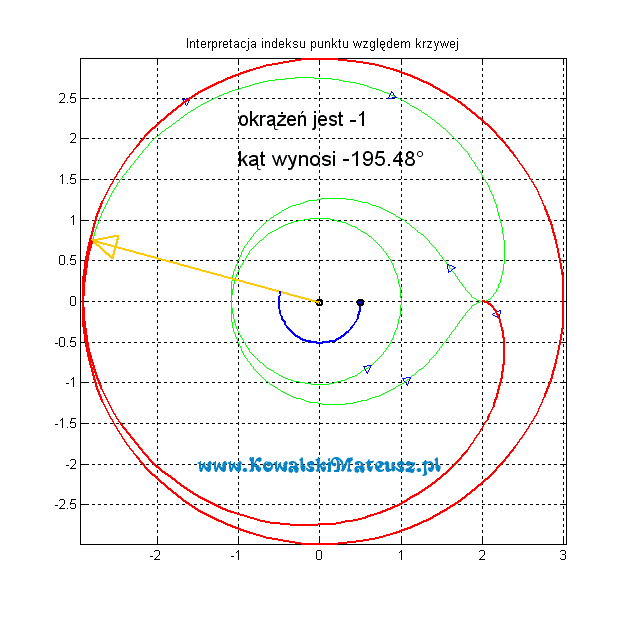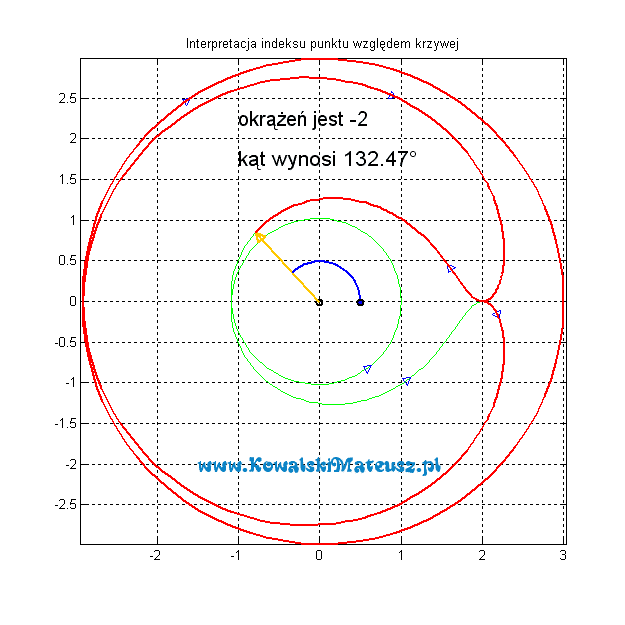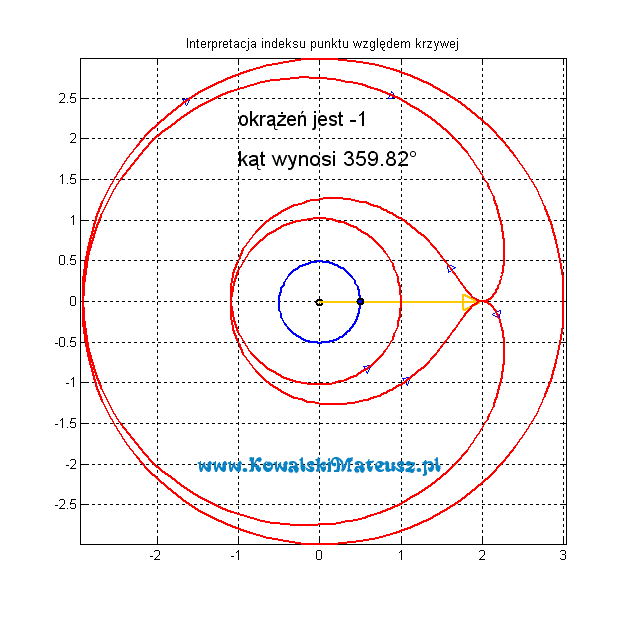
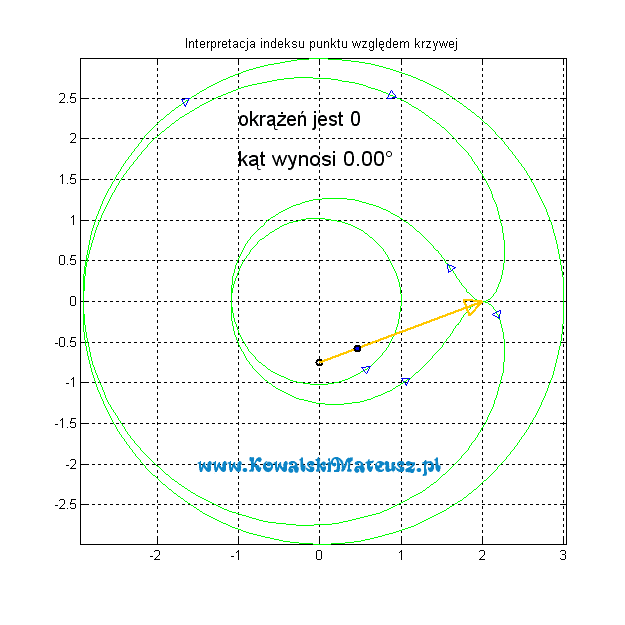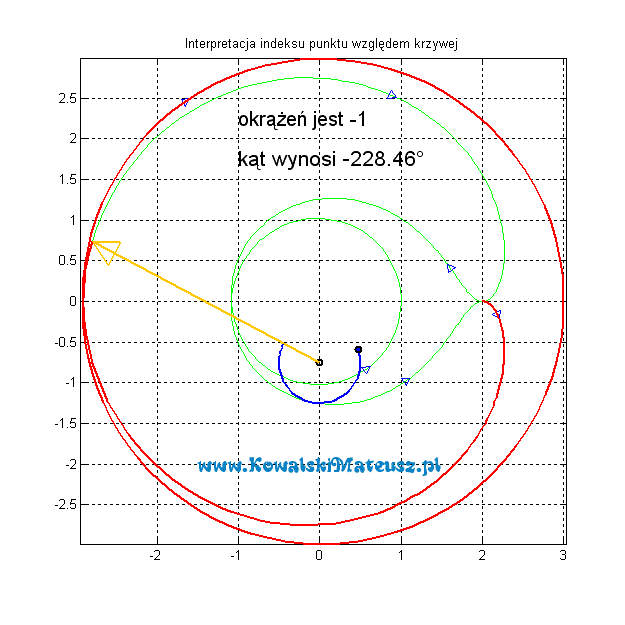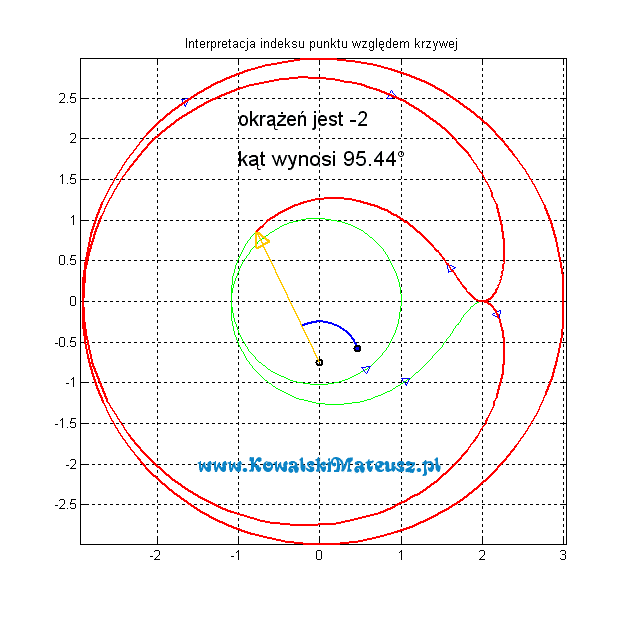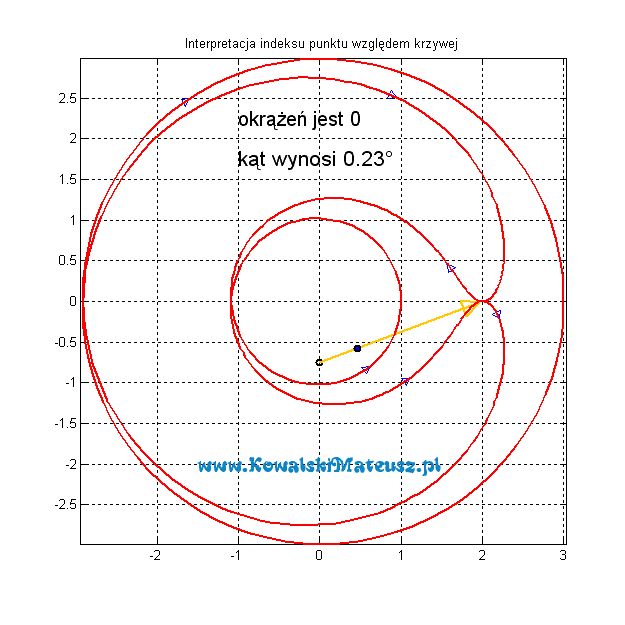
A teraz przy tej samej krzywej, ale zorientowanej przeciwnie.
Ale do czego takie abstrakcyjne liczenie kółek się przydaję?
ZASTOSOWANIE
Okazuje się, że ma to zastosowanie. W automatyce na podstawie stabilności transmitancji (funkcji przenoszenia) układu otwartego można wnioskować o stabilności układu zamkniętego jednostkową ujemną pętlą sprzężenia zwrotnego. Licząc liczbę obrotów na wykresie Nequista wokół punktu (-1,i0).
Sprowadzając problem do aspektu matematycznego, załóżmy, że mamy jakieś ![]() . Liczba niestabilnych (o dodatniej części rzeczywistej lub jak kto woli leżących w prawej półpłaszczyźnie) biegunów wynosi P. Jest pytanie jaka będzie liczba niestabilnych biegunów dla
. Liczba niestabilnych (o dodatniej części rzeczywistej lub jak kto woli leżących w prawej półpłaszczyźnie) biegunów wynosi P. Jest pytanie jaka będzie liczba niestabilnych biegunów dla ![]() . Otóż odpowiedź wcale nie musi być prosta, a często jest nawet trudna. Jednak wykorzystując indeks punktu względem krzywej można na ten problem odpowiedzieć.
. Otóż odpowiedź wcale nie musi być prosta, a często jest nawet trudna. Jednak wykorzystując indeks punktu względem krzywej można na ten problem odpowiedzieć.
Co warte uwagi nie wyznaczymy poszczególnych biegunów lecz będziemy znali tylko ich liczbę.
Analiza wygląda następująco:
Dane jest ![]()
Liczba niestabilnych biegunów wynosi 1 (P=1), bo tylko biegun (pierwiastek mianownika) ![]() ma cześć rzeczywistą dodatnią. A skąd weźmiemy krzywą? A no stąd. Mając
ma cześć rzeczywistą dodatnią. A skąd weźmiemy krzywą? A no stąd. Mając ![]() i uwzględniając tylko zmienność po osi urojonej, czyli podstawiając
i uwzględniając tylko zmienność po osi urojonej, czyli podstawiając ![]() , mamy
, mamy ![]() wyznaczając cześć rzeczywistą i urojoną i przyporządkowując je w ten sposób
wyznaczając cześć rzeczywistą i urojoną i przyporządkowując je w ten sposób ![]() oraz
oraz ![]() uzyskamy parametryzację krzywej. Każdy punkt krzywej jest podany przez
uzyskamy parametryzację krzywej. Każdy punkt krzywej jest podany przez ![]() , każdej
, każdej ![]() odpowiada jeden punkt krzywej. Zaś
odpowiada jeden punkt krzywej. Zaś ![]() zmienia się od
zmienia się od ![]() do
do ![]()
Tak na marginesie taki wykres nazywa się wykresem Nyquista. Liczba takich obiegów tej krzywej wokół punktu (-1,0i) dla ![]() zmieniającej się od
zmieniającej się od ![]() do
do ![]() zgodnie z ruchem wskazówek zegara oznaczmy przez N. Zauważ, że
zgodnie z ruchem wskazówek zegara oznaczmy przez N. Zauważ, że ![]() . W naszym przypadku jest to
. W naszym przypadku jest to ![]() . Wykonując prosty rachunek
. Wykonując prosty rachunek ![]() uzyskujemy
uzyskujemy ![]() . Teraz wartość
. Teraz wartość ![]() mówi o liczbie biegunów w prawej półpłaszczyźnie zespolonej układu zamkniętego.
mówi o liczbie biegunów w prawej półpłaszczyźnie zespolonej układu zamkniętego. ![]()
Sprawdźmy, że rzeczywiście
Dla ![]() bieguny to:
bieguny to:
![]()
Dla ![]() bieguny to w przybliżeniu:
bieguny to w przybliżeniu:
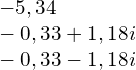
Czyli wszystko się zgadza.










Świetne animacje, dzięki! W sam raz na szybką powtórkę przed egzaminem dyplomowym, który mam za parę dni 😉
Bardzo się cieszę, że ten artykuł Ci pomógł.
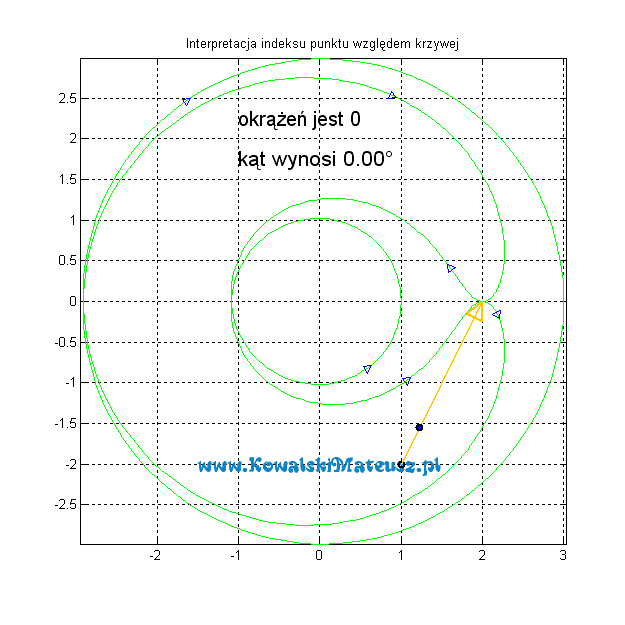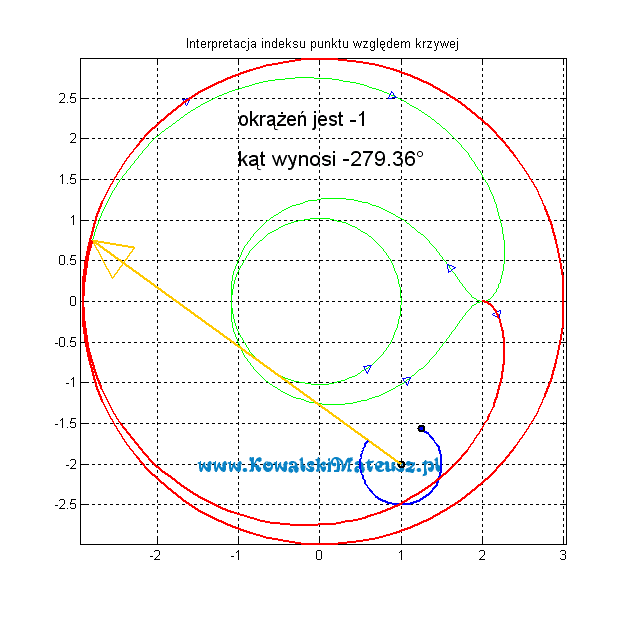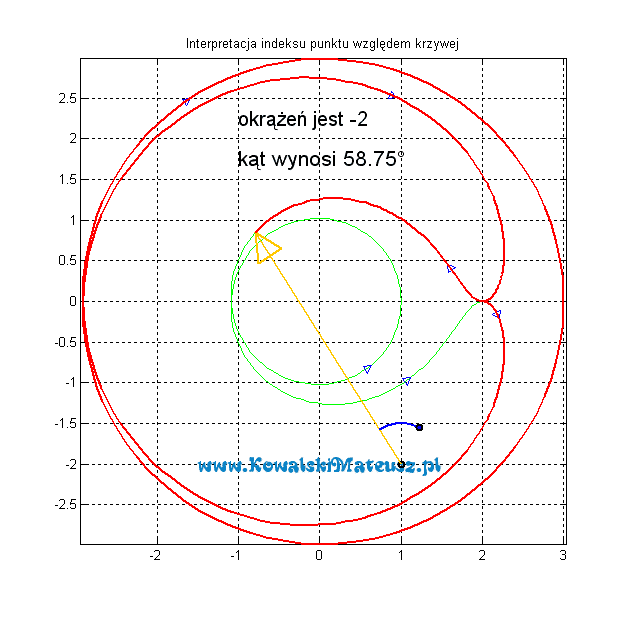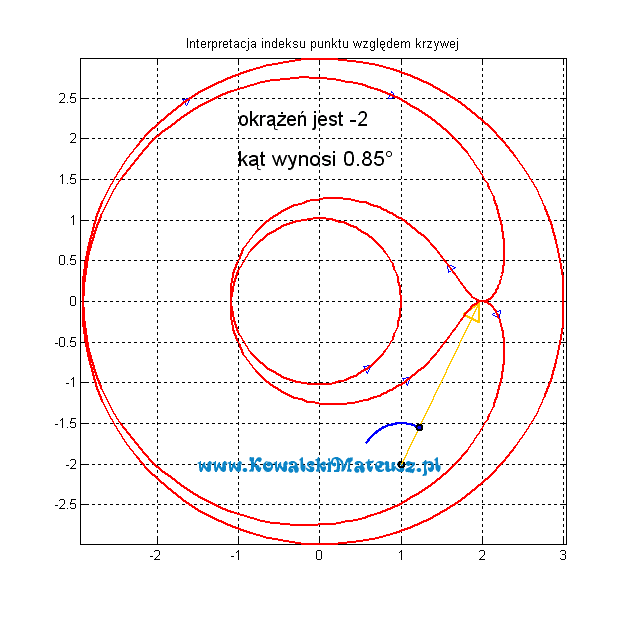
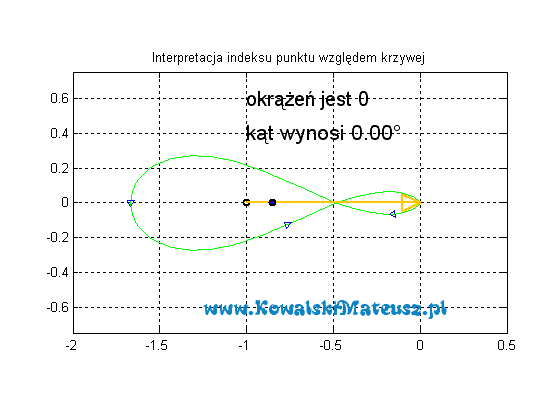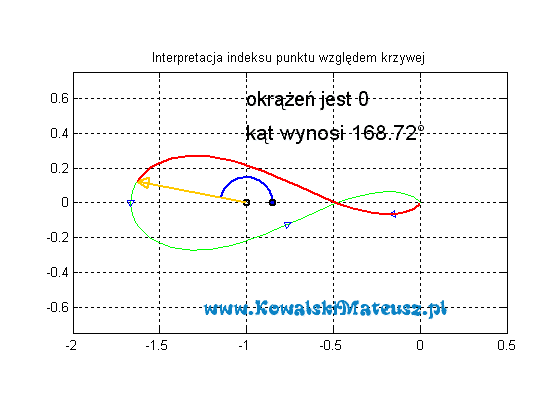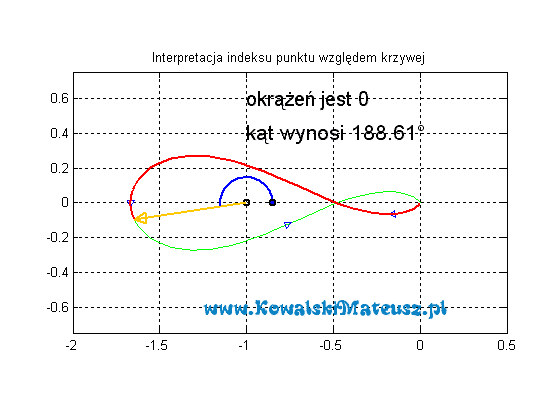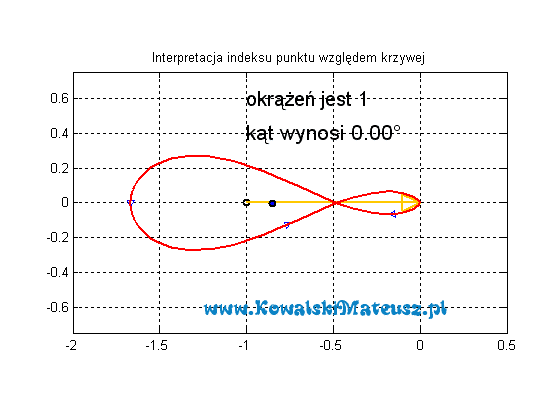
A co w sytuacji gdy punkt dla którego liczymy indeks nie znajduje się wewnątrz wykresu?
Robi się to dokładnie tak samo, a indeks będzie zawsze wynosił 0.
Dzięki